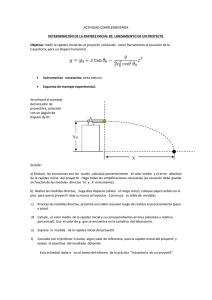
Práctica de Laboratorio PÉNDULO BALÍSTICO (COLISIONES)
Anuncio

! –– % & " !$ # # $! !$ 1. INTRODUCCIÓN. Los principios de conservación son fundamentales para la Física. Por medio de estos principios es posible estudiar y predecir la evolución en el tiempo de muchos sistemas. En el caso específico de la Mecánica, son de gran importancia los principios de conservación de la energía, conservación del momentum lineal y conservación del momentum angular. En esta práctica se utilizará el principio de conservación del momentum lineal y el principio de conservación de la energía mecánica para estudiar el funcionamiento de un péndulo balístico. Este es un dispositivo clásico que permite medir la rapidez de disparo un proyectil. Utilizando un péndulo balístico (Figura 1), un proyectil (balín) de masa m se dispara con rapidez vb, y al chocar contra el péndulo queda incrustado en él. Como resultado del impacto el conjunto péndulo-proyectil oscila alrededor del punto de suspensión alcanzando una altura máxima ∆h (Figura 2) sobre el punto donde ocurrió la colisión. De la altura ∆h (que en adelante le llamaremos h) alcanzada por el péndulo podemos medir su energía potencial. Esta a su vez es igual a la energía cinética del sistema justo después del choque, si despreciamos la fricción en el pivote del péndulo. No es posible igualar la energía cinética del péndulo justo antes del choque a la energía cinética del proyectil justo después de él, pues la colisión es inelástica. Sin embargo, dado que en toda colisión se conserva el momento lineal (cantidad de movimiento), si pueden igualarse los momentos lineales del sistema proyectil – péndulo, justo antes y justo después del choque, asi: m vb = M vp donde M es la masa combinada del péndulo y el proyectil incrustado, y vp es la rapidez del péndulo justo después del choque. La energía cinética del sistema en éste último instante es K = ½(M vp2) que a su vez es igual a la energía potencial que alcanza el sistema en su altura máxima: U = Mg∆h = MgRcm(1 – cosθ) donde Rcm es la distancia desde el eje de rotación del péndulo (punto de suspensión) hasta su centro de masa, y θ es el ángulo máximo respecto a la vertical que alcanza el péndulo en su oscilación. Ejercicio preliminar. De las ecuaciones anteriores demuestre que la rapidez del proyectil puede expresarse como vb =(M/m) 2 gRcm (1 − cos θ ) (1) Podemos ver que la rapidez inicial del proyectil puede determinarse a partir de la medición de las masas, Rcm y el ángulo de oscilación máxima θ. 2. PROCEDIMIENTO. 2.1 Determinación de la Rapidez Inicial a partir de los Principios de Conservación. Antes de iniciar las mediciones usted debe alinear el sistema para asegurar que el proyectil se incruste en el péndulo. Así mismo nivele el sistema y asegúrelo a la mesa de trabajo. 2.1.1 Dispare el proyectil unas 10 veces y registre la altura máxima del péndulo en cada caso. Tome el valor medio de h con su respectiva incertidumbre. 2.1.2 Baje el péndulo del soporte, obtenga su masa combinada M y la masa m del proyectil. 2.1.3 Para determinar Rcm, con el proyectil dentro del péndulo desmontado, determine su centro de masa balanceándolo horizontalmente con una cuerda (Figura 3) o sobre el filo de una regla, midiendo luego la distancia entre el punto de soporte del péndulo y este punto de equilibrio. 2.1.4 Con los datos anteriores y usando la expresión (1) calcule la rapidez inicial (vb) del proyectil, con su respectiva incertidumbre. Use para sus cálculos el valor g = (977 ± 10) cm/s2. 2.1.5 Haga una discusión sobre las transformaciones de energía ocurridas en las distintas etapas del fenómeno observado. 1 2.2 Determinación De La Rapidez Inicial Por Métodos Cinemáticos. 2.2.1 Ahora prepare el sistema para el tiro parabólico, ajustando el ángulo de lanzamiento a 0° de forma que el balín sea disparado horizontalmente (Figura 4). Coloque el dispositivo en el borde de la mesa y no lo mueva del sitio escogido mientras realiza el experimento. Ubique el péndulo de tal forma que no interfiera con la trayectoria del proyectil. Dispare el proyectil y observe el punto donde golpea el suelo o la pared. Pegue en ese sitio una hoja de papel con otra hoja de papel carbón encima. De esta manera podrá registrar los impactos del proyectil sobre el piso (o la pared). 2.2.2 Repita 10 veces el disparo. Mida el alcance promedio X del proyectil y la altura Y del punto de lanzamiento. Estime la incertidumbre para cada una de estas mediciones. 2.2.3 Tomando el origen de coordenadas cartesianas en el punto de salida del balín (Ver Figura 4), el eje X positivo hacia la derecha y el eje Y positivo hacia abajo, DEMUESTRE, a partir de las ecuaciones cinemáticas del movimiento parabólico, que ( X = Vb t ) y ( Y = reemplácelo en Y para obtener que Vb = 1 g t 2 ). Despeje el tiempo de la ecuación para X, 2 gX 2 , y de sus medidas del alcance X y la altura Y, determine la 2Y rapidez inicial vb del proyectil, con su incertidumbre. 3 PREGUNTAS. 3.1 De las mediciones de vb realizadas anteriormente (2.1 y 2.2) diga cuál de los dos resultados podría considerarse como un valor convencionalmente verdadero. En su discusión tenga en cuenta las diferencias entre cada modelo teórico y la realidad experimental, las posibles fuentes de error sistemático, así como la incertidumbre de cada resultado. Una vez escogido el valor convencionalmente verdadero determine el error y el porcentaje de error del otro valor. 4. PREPARACIÓN. Revise los principios de Conservación del Momentum Lineal, Conservación de la Energía, tipos de colisiones y cinemática del Movimiento Parabólico. 2 A B C D E GRUPO F G H I J PROFESOR FECHA Apellidos y Nombres Código INTEGRANTES DEL GRUPO Tabla No. 1 (1) (3) (5) (7) (9) (h ± ∆h ) (cm) = Medidas de Altura y su Incertidumbre (2) (4) (6) (8) (10) (M ± ∆M ) (gr) = (m ± ∆m ) (gr) = (Rcm ± ∆Rcm ) (cm) = (Vb ± ∆Vb ) (cm/s) = Tabla No. 2 (1) (3) (5) (7) (9) (X ± ∆X ) (cm) = Medidas del Alcance X y su Incertidumbre (2) (4) (6) (8) (10) (Y ± ∆Y ) (cm) = (Vb ± ∆Vb ) (cm/s) = Error de Vb (cm/s) % de Error de 3 Vb