Curvas de Lissajous
Anuncio

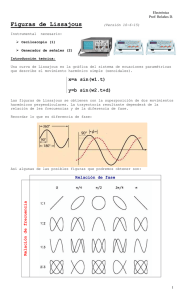
Figuras de Lissajous Aunque estas figuras se atribuyen al físico francés Lissajous, hacia el año 1815 ya las había descrito Bowditch. Jules Antoine Lissajous (1833-1880) Nathaniel Bowditch(1773-1838) Una curva de Lissajous es la gráfica del sistema de ecuaciones paramétricas que describe el movimiento harmónico simple. x=a sin(w1t) y=b sin(w2t+d) Las figuras de Lissajous se obtienen con la superposición de dos movimientos harmónicos perpendiculares. La trayectoria resultante dependerá de la relación de les frecuencias y de la diferencia de fase. Lissajous utilizó sonidos de diferentes frecuencias para hacer vibrar un espejo. Un rayo de luz reflejado en el espejo dibujaba figuras diferentes según la frecuencia de los sonidos. Lissajous primero reflejaba un rayo de luz en un espejito pegado a un diapasón que vibraba y, a continuación, otro espejito en otro diapasón también vibrando. El rayo se proyectaba entonces en una pantalla creando una figura, la forma de esta dependía de la amplitud y frecuencia de las vibraciones y su relación. Si los dos diapasones tienen la misma frecuencia entonces el dibujo resultante es una elipse. Antes de la existencia de los medidores digitales de frecuencia y las antenas phaselocked, las figuras de Lissajous se utilizaban para determinar las frecuencias de sonidos y señales de radio. Una señal de frecuencia conocida se aplicaba al eje horizontal de un osciloscopio y la señal a medir se aplicaba en el eje vertical. La figura resultante era función de la razón de ambas frecuencias.