Ω = → Ω = Ω = Ω + Ω = + = 8 8 1 24 3 24 1 12 1 1 1 1 RRRR Ra Ω
Anuncio

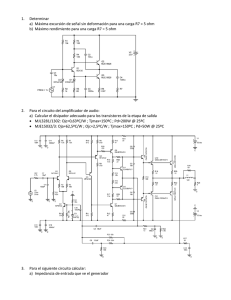
Ejercicio 2 – Hoja de ejercicios de circuitos. Averigua qué marcarán los amperímetros y los voltímetros intercalados en el siguiente circuito, si sabemos que el voltímetro V1 marca 12 V: Como la diferencia de potencial medida en V1 está aplicada sobre todo el circuito, se calculará la resistencia equivalente de todo el circuito y mediante la ley de Ohm se podrá calcular la intensidad de corriente que circula por el conductor “principal” del circuito y que será lo que señalen los amperímetros A1, A2 y A5. Req Cálculo de la resistencia equivalente del circuito: Ra El circuito tiene tres resistencias. Las dos primeras, R1 y R2 están en paralelo y este agrupamiento, a su vez, en serie con R3. Primeramente se calcula el valor de la resistencia equivalente de las dos en paralelo, Ra, y, a continuación, se le suma el valor de R3, al estar en serie. De esta manera se obtiene el valor de la resistencia equivalente del circuito, Req. 1 1 1 1 1 3 1 = + = + = = Ra R1 R2 12 Ω 24 Ω 24 Ω 8 Ω → Ra = 8 Ω Req = Ra + R3 = 8 Ω + 4Ω = 12 Ω Cálculo de la intensidad que indican A1, A2 y A5: Aplicando la ley de Ohm, para la resistencia equivalente de todo el circuito se obtiene: I= V 24 V = =1 A R 24 Ω I = I1 = I2 = I5 = 1 A Cálculo de la diferencia de potencial marcada por V3: La resistencia R3 es atravesada por toda la corriente que pasa por el conductor “principal”, es decir, 1 A. Utilizando la ley de Ohm: V3 = I ⋅ R3 = 1 A ⋅ 4 Ω = 4 V Cálculo de la diferencia de potencial marcada por V2: El voltímetro V2 marcará la caída de potencial que se produce en el agrupamiento de las dos resistencias en paralelo, aunque se sabe que sería el mismo que se produce en cada una de las ramas. Se puede utilizar el valor de Ra y aplicar la ley de Ohm, ya que se ha obtenido que la intensidad que circula por el circuito es 1 A, y este agrupamiento en su conjunto es atravesado por esta intensidad. V2 = I ⋅ Ra = 1 A ⋅ 8 Ω = 8 V Cálculo de la intensidad indicada A3 y A4: La corriente que circula por el circuito, al llegar a las dos resistencias en paralelos, se divide pasando por cada una de ellas una intensidad de corriente distinta. Si se considera que el amperímetro A3 mide una intensidad I3 y el amperímetro A4 otra I4, se sabe que I = I3 + I4. Además, se ha calculado que la diferencia I =1A de potencial V2 vale 8 V y es la misma para cada I3 una de las ramas donde se encuentran las resistencias R1 y R2. I4 Por lo tanto, aplicando la ley de Ohm a cada una de las ramas se puede obtener la intensidad que circula por ellas: V2 = 8 V - Para calcular el valor que marca el amperímetro A3 se aplica la ley de Ohm a la resistencia R1, ya que son atravesados por la misma intensidad: I3 = - V2 8V 2 = = A = 0,67 A R1 12 Ω 3 Para calcular el valor que marca el amperímetro A4 se aplica la ley de Ohm a la resistencia R2, ya que son atravesados por la misma intensidad: I4 = V2 8V 1 = = A = 0,33 A R2 24 Ω 3 Como se puede apreciar, la suma de I3 e I4, daría el valor de la intensidad, 1 A, que circula por el conductor antes y después de dividirse en las dos ramas.