8- Inducción electromagnética 8.1 Experiencias de Faraday y Henry
Anuncio
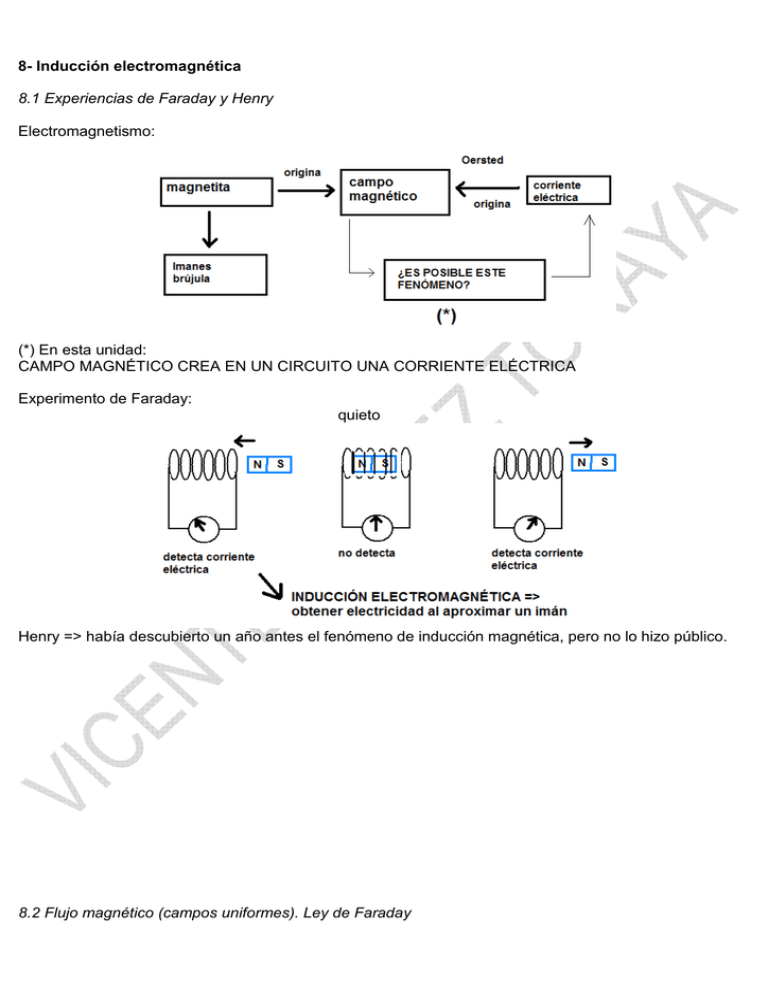
8- Inducción electromagnética 8.1 Experiencias de Faraday y Henry Electromagnetismo: (*) En esta unidad: CAMPO MAGNÉTICO CREA EN UN CIRCUITO UNA CORRIENTE ELÉCTRICA Experimento de Faraday: quieto Henry => había descubierto un año antes el fenómeno de inducción magnética, pero no lo hizo público. 8.2 Flujo magnético (campos uniformes). Ley de Faraday + Observación: sólo se produce inducción si hay movimiento relativo => imán => solenoide + Inducción eléctrica (electrostática)-inducción electromagnética (magnética): + FLUJO MAGNÉTICO: => Líneas de campo que atraviesan una superficie Flujo magnético => “a través de una superficie se define como una magnitud equivalente al resultado de multiplicar escalarmente los vectores intensidad de campo magnético y superficie”: φ = B·s = B·s·Cosα Unidad de flujo: Weber (Wb) = 1 T·m2 Si disponemos de N espiras: φTOTAL = N ·B·s = N ·B·s·Cosα Conclusión => “sólo si varía el número de líneas de campo magnético que atraviesan el circuito se detecta en él una corriente inducida” Ejemplo: εmedia Relación cuantitativa entre la fuerza electromotriz (fem) inducida y la rapidez con que varía el flujo magnético (N espiras): ∆φ ⇒ Ley de la inducción de Faraday-Henry ε media = N · ∆t (ε proporcional a la rapidez con que cambia el flujo a través del inducido) 8.3 Ley de Lenz + Ley de Faraday-Henry: calcula el valor εmedia pero no indica el sentido de la corriente inducida. => Lenz soluciona el problema: “El sentido de la corriente inducida es tal que, el campo magnético que dicha corriente produce tiende a oponerse al cambio de flujo creado por la causa que lo originó” Corriente inducida, Binducido: La corriente inducida es tal que se opone a la variación que crea el inductor Ley de Lenz: dφ flujo _ crece ⇒ dt > 0 → ε < 0 dφ ε = − N · ⇒ signo − indica ⇒ dφ dt flujo _ decrece ⇒ <0→ε >0 dt Ejemplos: obtener el campo y corriente inducida 8.4 Casos importantes de inducción Movimiento de un conductor en un B uniforme: La carga negativa se acumula en la parte inferior: Se establece una ddp entre sus extremos Interpretación según la ley Faraday-Lenz: Parte conductora móvil forma parte de un circuito, Al moverse el Ф varía: dφ = B·ds = B·ds·Cos 0º = B·ds = B·L·dx = = B·L·v·dt dφ = B·L·v = ε dt Problemas: CS04,CS06,PJ07,PS08,CS2010-2 8.5 Aplicaciones básicas: generador eléctrico Generadores => obtener energía eléctrica a partir de la inducción electromagnética: Energía cinética Energía eléctrica ALTERNADOR DINAMO (generadores de electricidad) => transformación contraria al motor eléctrico. Tensión que nos produce un alternador => proceso: Giro espira (bobina) => varía θ => varía Ф dentro de un B uniforme => circuito se opone a la modificación (Faraday-Lenz) => da lugar a una Iinducida o εinducida … => nos produce una tensión o corriente alterna (no corriente continua como en las pilas a V constante). En Europa la tensión de alterna es de 50 Hz. TEMA V: FÍSICA MODERNA 9.- Física cuántica 9.1 Naturaleza de la luz + Los antecedentes de la Física cuántica están relacionados con la naturaleza de la luz. + Dos modelos (s.XVII): Cualquier modelo sobre la luz debe explicar => propagación rectilínea, reflexión, refracción, dispersión de los colores-prisma, difracción, interferencias, … (1º) Modelo corpuscular: - Newton - Propagación rectilínea => luz como haz de partículas Explica => la transmisión de la luz en el vacío => refracción (distinta v según n) (2º) Modelo ondulatorio: - Huygens - onda longitudinal necesita medio material => éter - luz consistirá en una vibración de la materia (emisor-receptor) s.XVII => Hooke: ondas transversales s.XVIII => Young: interferencias luminosas s.XIX => Fresnel. Desarrollo una teoría sobre el carácter ondulatorio de la luz => interferencias, difracción, … 9.2 Antecedentes de la hipótesis cuántica (1) ESPECTROS ATÓMICOS: => Cada sustancia conocida al colocarla en la llama de un mechero emitía luz de un color determinado => cada elemento químico da un espectro de emisión característico: ∆E = h·ν Espectro de emisión: (2) RADIACIÓN DE UN CUERPO NEGRO: + La energía que recibimos del Sol nos llega por radiación. + Los cuerpos calientes (a cierta temperatura T) emiten energía a su entorno por radiación electromagnética. Ejemplo: hierro + CUERPO NEGRO (emisor ideal): => bloque de metal al que le hemos hecho una cavidad con un orificio. Proceso: Al calentar el metal a una determinada temperatura, por la pequeña abertura escapa una radiación Un cuerpo negro se comporta como el emisor ideal => la energía radiante está en equilibrio con las paredes. aumenta tensión => aumenta brillo filamento (significa que aumenta la temperatura) => color luz emitida: rojiza => amarilla => blanca + Curvas de emisión del cuerpo negra a diferentes temperaturas: 1m = 1010 angstrom Conclusiones: - un cuerpo caliente emite más energía que uno menos caliente - A medida que aumenta la temperatura disminuye la λ a la que se produce la emisión (% mayor dentro del espectro visible). Ejemplo: bombilla => λrojo>λamarillo (3) EFECTO FOTOELÉCTRICO: LEYES EXPERIMENTALES + Hertz: efecto Hertz o efecto fotoeléctrico: estudiaba descargas eléctricas entre dos electrodos => observó que la descarga se producía más fácilmente si iluminaba uno de los electrodos (luces diferentes, la mejor la ultravioleta). Estudio experimental del efecto fotoeléctrico: => emisión de electrones que son arrancados del metal gracias a la energía debida a la luz incidente. CÉLULA FOTOELÉCTRICA: Proceso: Luz incide en el cátodo Arranca electrones Son acelerados por la ddp del circuito hacia el ánodo El galvanómetro (G) detecta corriente débil Leyes que se obtuvieron con el dispositivo anterior y utilizando luz monocromática (luz de única frecuencia): 1- עi luz incidente > ע0 (frecuencia umbral del metal) => SE PRODUCE EL EFECTO FOTOELÉCTRICO si עi luz incidente < ע0 (frecuencia umbral del metal) => no arranca electrones => NO SE PRODUCE EL EFECTO FOTOELÉCTRICO 2- Efecto es instantáneo si se produce (incluso por poca energía por unidad de tiempo => bajas ∆E ) intensidades luminosas: I = ∆s∆t 3- La corriente electrónica que circula por la célula depende de la tensión aplicada, V: Aumenta V => aumenta I hasta un límite: corriente de saturación iS de la fotocorriente iS es proporcional a la intensidad de la luz incidente en la fotocélula. 4- Si invertimos la polaridad de la batería y V se hace negativa, la fotocorriente baja y se anula para V=-V0 => POTENCIAL DE CORTE O DE FRENADO. + Interpretación del efecto fotoeléctrico: Luz que actúa sobre distintos electrones de un metal, energía mínima para extraer electrones => W e = trabajo de extracción = trabajo necesario para que un electrón quedase en reposo fuera del metal. We relacionado con la energía de ionización (E.I.) => ejemplos: Potasio => bajo 2 eV Aluminio => 4,2 eV + El modelo ondulatorio no explica el efecto fotoeléctrico: - Luz incidente “continua” de energía => tarde o temprano se producirá emisión - No explica el efecto instantáneo: Iluminación débil produce el efecto (ya que sólo depende de la frecuencia de la luz) - aumenta la intensidad de la iluminación (aumenta la energía) => independiente de la frecuencia => no habría frecuencia de corte. 9.3 Hipótesis de Planck + Estudios sobre el cuerpo negro => la radiación emitida está en equilibrio con los osciladores que forma la pared de la cavidad. Planck: => un átomo se comporta como un oscilador armónico cuya frecuencia natural de vibración es ;עdicho oscilador sólo puede variar su energía en cantidades múltiplos de la cantidad E1, que depende de la frecuencia de vibración: E1=h·ע h => constante de Planck: h = 6,626·10-34 J·s El oscilador emite o absorbe radiación según el siguiente cambio energético: |∆Eoscilador|=n·h·ע n = número entero La energía está cuantizada => la energía del oscilador sólo puede variar un número entero de veces. + Hipótesis cuántica de Einstein: - Planck => energía emitida en forma de cuantos o paquetes, pero luego, la energía se distribuía uniformemente por el frente de onda (según la física clásica). - Aportación de Einstein => hipótesis cuántica: => LA RADIACIÓN SE EMITE Y SE CAPTA POR CUANTOS O PAQUETES La energía electromagnética que se propaga con la luz está distribuida de forma discontinua => un haz de luz consta de un número entero de paquetes de energía o cuantos = FOTONES (Lewis) => “teoría de los cuantos de luz” FOTÓN = una partícula de masa en reposo cero y cuya velocidad es la de la luz, su energía es E=h·ע, donde = עfrecuencia de la radiación. Comparación: 9.4 Efecto fotoeléctrico + Comparación: + Hipótesis de Einstein: - La luz está compuesta por corpúsculos o fotones cuya energía: E = h · ( עhipótesis cuántica) - El efecto fotoeléctrico se produce cuando un electrón interacciona con un único fotón, pero, sólo si, la energía del fotón es suficiente para arrancarlo del metal. Explicación de los hechos experimentales: a) Frecuencia umbral o mínima ע0: Si E > W e = h · ע0 => los fotones arrancan electrones => se produce el efecto fotoeléctrico Si E < W e = h · ע0 => los fotones no arrancan electrones => no se produce el efecto fotoeléctrico b) Si baja la intensidad de la iluminación => baja el número de fotones => baja el número de electrones arrancados (si E > W e = h · ע0). c) El exceso de energía del fotón sobre el W e se transforma en Ec del electrón arrancado: Energía del fotón = energía de extracción + Ec E = W e + Ec Si ע0 es la frecuencia umbral => W e = h · ע0, y como E = h · ( עenergía del fotón incidente): h · = עh · ע0 + Ec luego, Ec = h·(ע – ע0) Problemas: CJ04,PS04,CJ05,PJ05,CJ07,PJ07,CS07,CJ08,PS08,PS09,CJ2010-1,CS2010-2 9.5 Dualidad onda-corpúsculo. Principio de incertidumbre (1) DUALIDAD ONDA-CORPÚSCULO: - Fenómenos luminosos: Modelo ondulatorio => interferencias, difracción, … Modelo corpuscular => efecto fotoeléctrico,… LUZ PARTÍCULA DUALIDAD Energía: E = m·c2 ONDA Frecuencia: c= λ T = λ ·ν ⇒ ν = c λ E = h·ע Longitud de onda: λ Caracterizada por: - velocidad de propagación -λ -ע -… Momento lineal: p=m·v Caracterizada por: - cantidad de movimiento o momento lineal - posición … Luz: v=c p=m·c E m= 2 c E p = 2 ·c c E p= c h·ν p= c λ= ν c p= h λ comportamiento dual para la luz: ONDA-PARTÍCULA - Analizado por Louis de Broglie. - Bohr lo analizó en el comportamiento de los electrones => generalizó la dualidad de la luz (fotones) a los electrones y por extensión a todos los corpúsculos. HIPÓTESIS DE DE BROGLIE: “Toda partícula (fotón, electrón, …) de cantidad de movimiento p lleva asociada una onda cuya λ cumple h la ecuación p = ” λ (2) PRINCIPIO DE INDETERMINACIÓN O INCERTIDUMBRE: Física cuántica => mecánica cuántica. Mecánica cuántica => es la única capaz de explicar el comportamiento de la naturaleza a escala atómica o inferior (estructura del átomo, radiactividad, enlace químico, láser, …) - Schrödinger => dualidad onda-partícula: Describe al electrón como una función de onda ψ (r , t ) para analizar el movimiento del electrón alrededor del núcleo. - Born: Función de onda ψ (r , t ) asocia una función de probabilidad que nos da la probabilidad de encontrar la partícula (electrón) dentro de un elemento de volumen dv situado alrededor del punto r Ejemplo: PRINCIPIO DE INCERTIDUMBRE O INDETERMINACIÓN DE HEISENBERG: Mecánica clásica => permite determinar posiciones o velocidades de una partícula en un instante (ley de la gravitación universal => posición y velocidad de los planetas). Universo cuántico (nivel atómico) y desde el punto de vista de la dualidad onda-corpúsculo implica aceptar el principio de indeterminación de Heisenberg: “No se puede determinar simultáneamente con precisión absoluta la posición y el momento lineal de una partícula” Es una propiedad intrínseca de la naturaleza dual de las partículas. Problemas: CJ06,CJ09,PS06




