ESCUELA TÉCNICA SUPERIOR DE INGENIEROS
Anuncio
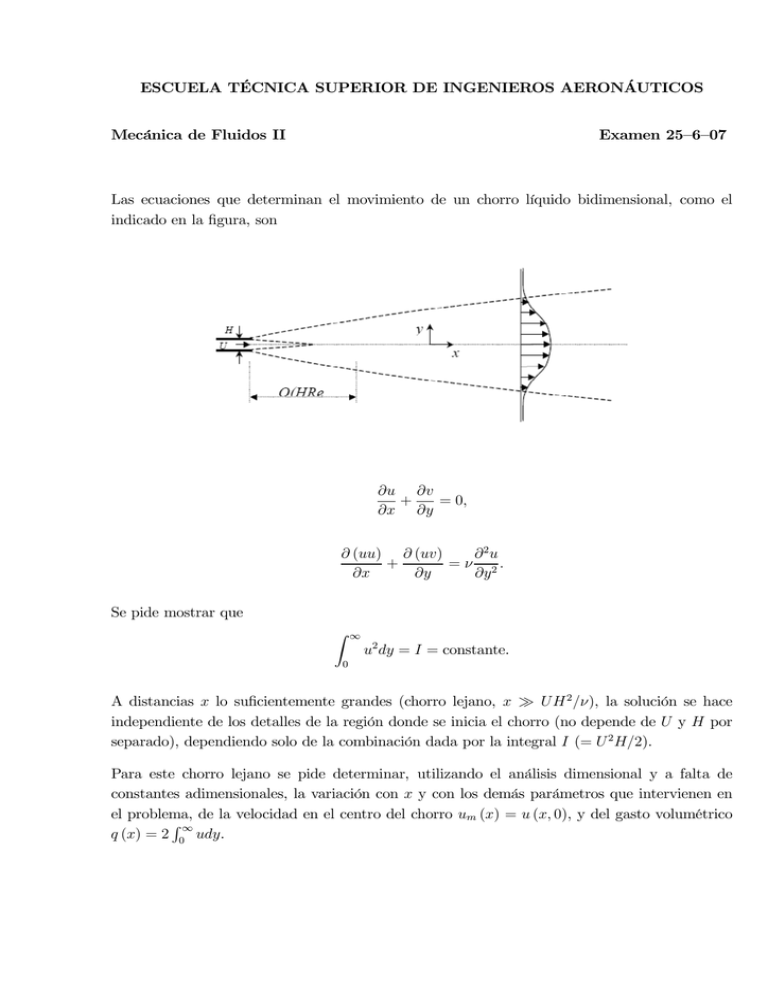
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS AERONÁUTICOS Mecánica de Fluidos II Examen 25—6—07 Las ecuaciones que determinan el movimiento de un chorro líquido bidimensional, como el indicado en la figura, son ∂u ∂v + = 0, ∂x ∂y ∂ (uu) ∂ (uv) ∂ 2u + = ν 2. ∂x ∂y ∂y Se pide mostrar que Z ∞ u2 dy = I = constante. 0 A distancias x lo suficientemente grandes (chorro lejano, x À UH 2 /ν), la solución se hace independiente de los detalles de la región donde se inicia el chorro (no depende de U y H por separado), dependiendo solo de la combinación dada por la integral I (= U 2 H/2). Para este chorro lejano se pide determinar, utilizando el análisis dimensional y a falta de constantes adimensionales, la variación con x y con los demás parámetros que intervienen en el problema, de la velocidad en el centro del chorro um (x) = u (x, 0), y del gasto volumétrico R∞ q (x) = 2 0 udy. SOLUCIÓN De la ecuación de cantidad de movimiento, multiplicada por dy e integrada entre 0 e ∞ se obtiene Z ∞ Z ∞ Z ∞ ∂u d 2 u dy + d(uv) = d(ν ), dx 0 ∂y 0 0 y dado que u → 0 en y → ∞; v = 0 y ∂u/∂y = 0 en y = 0, la ecuación anterior se reduce a Z ∞ Z ∞ d 2 u dy = 0; u2 dy = I = constante. dx 0 0 Las ecuaciones de continuidad y cantidad de movimiento se pueden escribir independientes de √ √ ν si se utilizan las variables y/ ν y v/ ν. En efecto, se tiene √ ∂u ∂ (v/ ν) √ = 0, + ∂x ∂ (y/ ν) √ ∂ 2u ∂ (uu) ∂ [u (v/ ν)] √ = + √ 2, ∂x ∂ (y/ ν) ∂ (y/ ν) mientras que las condiciones de contorno quedan Z ∞ ¡ √ ¢ √ u2 d y/ ν = I/ ν, 0 √ √ √ en y/ ν → ∞ es u = 0 y en y/ ν = 0 es v/ ν = 0 y ∂u √ = 0. ∂ (y/ ν) Por lo tanto, la solución será de la forma µ µ ¶ ¶ y y I v I u = f1 x, √ , √ ; √ = f2 x, √ , √ , ν ν ν ν ν y utilizando el análisis dimensional se tiene # " u (νx)1/3 yI 1/3 = Φ (η) , =Φ I 2/3 (νx)2/3 de modo que en el centro del chorro se tiene µ I2 um = Φ (0) νx ¶1/3 , donde Φ (0) es una constante adimensional a determinar resolviendo el problema planteado (la solución proporciona Φ (0) = 0.4543). Para determinar el gasto volumétrico se tiene Z Z ∞ 1/3 udy = 2 (Iνx) q=2 R∞ 0 ∞ Φ (η) dη = K (Iνx)1/3 , 0 donde K = 2 0 Φ (η) dη es una constante adimensional que se obtiene de la solución del problema (K = 62/3 = 3.302).











