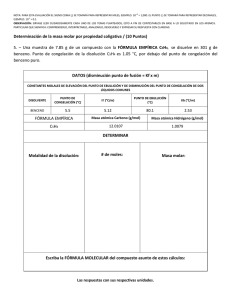
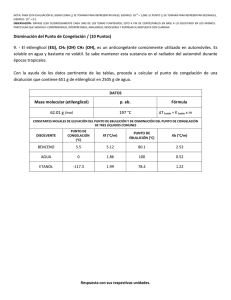
Congelación.

Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Tema 9
Congelación.
Objetivos
•
Definir la operación de congelación, su utilidad y su ámbito de aplicación.
•
Estudiar los fenómenos de transferencia del calor que tienen lugar durante la
congelación.
•
Aprender a estimar tiempos de congelación.
•
Conocer la influencia de la geometría de los alimentos en el tiempo de
congelación.
•
Estudiar los diferentes tipos de congelación y los medios de transmisión del
calor empleados.
•
Describir el equipo de congelación utilizado más frecuentemente.
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Índice del tema
1
CONCEPTO DE CONGELACIÓN ...........................................................................................3
2
CINÉTICA DEL PROCESO DE CONGELACIÓN .......................................................................5
2.1
2.2
2.3
Descripción rigurosa del problema y simplificaciones aceptadas...............................7
Determinación de los tiempos de preenfriamiento y atemperado. ...............................8
Determinación del tiempo de congelación en geometría plana .................................10
2.3.1
2.3.2
2.4
2.5
2.6
2.7
3
Solución rigurosa de Newman .......................................................................................... 10
Solución aproximada de Plank.......................................................................................... 12
Estimación de la velocidad de congelación ...............................................................13
Influencia de la resistencia térmica externa en el tiempo de congelación. ................14
Estimación del tiempo de congelación en otras geometrías. .....................................15
Estimación del tiempo total de congelación. Otros métodos......................................18
PROPIEDADES TÉRMICAS DE LOS ALIMENTOS. ................................................................18
3.1
Calor latente de congelación, capacidad calorífica de los alimentos y conductividad
térmica. ......................................................................................................................19
3.2 Temperatura del punto de congelación......................................................................19
3.3 Contenido en agua libre de los alimentos congelados ...............................................21
4
ASPECTOS TECNOLÓGICOS DE LA CONGELACIÓN ............................................................24
4.1
4.2
Calidad de los alimentos congelados .........................................................................24
Métodos de congelación y equipos industriales .........................................................25
4.2.1
4.2.2
4.2.3
4.2.4
5
Congelación por contacto directo: congeladores de placas ............................................... 25
Congelación por contacto con un líquido refrigerado: inmersión ..................................... 26
Congelación por contacto directo con un gas refrigerado ................................................. 27
Congeladores por contacto con líquido que se vaporiza: congeladores criogénicos ......... 29
DESCONGELACIÓN ..........................................................................................................30
2 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Congelación
1
Concepto de congelación
El empleo de bajas temperaturas es uno de los métodos más antiguos para conservar los
alimentos. Cuando las bajas temperaturas producen la solidificación del agua contenida en los
alimentos, esta deja de estar disponible para que en su seno se verifiquen las reacciones
químicas y bioquímicas que constituyen la degradación de lso alimentos.
El efecto combinado de las bajas temperaturas y la disminución de la actividad del agua
causan la inhibición total o parcial de los principales agentes responsables de la alteración de los
alimentos:
•
Crecimiento y actividad de los microorganismos
•
Actividades metabólicas de los tejidos animales y vegetales tras el sacrificio y
la recolección.
•
reacciones enzimática y químicas.
El empleo de bajas temperaturas en los alimentos ya sea para refrigerar o congelar,
permite alargar la vida útil, ya sean frescos o procesados, durante períodos de tiempo
relativamente largos manteniendo sus propiedades nutritivas y organolépticas. No obstante hay
que señalar que las diferencias fundamentales entre refrigeración y congelación (y las mayores
ventajas aportadas por la congelación cuando es necesaria y posible, claro) es la bajada de la
actividad del agua que tiene lugar por su solidificación.
De hecho la mayor efectividad, en la conservación de alimentos, conseguida por
métodos de congelación a baja temperatura como la ultracongelación y la criocongelación, se
deben a su mayor homogeneidad y a que solidifican una mayor parte del agua, antes que a las
bajas temperaturas en sí mismas.
La aplicación del frío se basa en una de las operaciones básicas más empleadas en la
industria agroalimentaria: la transmisión del calor. En este caso a diferencia de la aplicación del
calor, el foco caliente es el alimento el cual cede su calor a un medio exterior frío.
REFRIGERACIÓN, es la reducción y el mantenimiento de la temperatura del
alimento por encima de su punto de congelación, siendo las temperaturas más habituales las
comprendidas entre 8ºC y –1ºC. La refrigeración sólo implica cambios en el calor sensible del
alimento. Al no ser muy grande el descenso de temperatura la inhibición de los principales
agentes responsables de la alteración de los alimentos es parcial. La refrigeración de los
alimentos alarga su vida durante un tiempo limitado de días o semanas.
CONGELACIÓN, se produce a consecuencia de un descenso de la temperatura del
alimento por debajo de su temperatura de congelación. Teniendo en cuenta que la temperatura
de congelación de los alimentos es por debajo de 0ºC (entre –5ºC y –2ºC, aproximadamente), la
temperatura normal (mínima) de conservación es de –18ºC. La congelación no sólo implica un
cambio de calor sensible del alimento, sino que también es necesario retirar el calor latente
3 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
asociado al cambio de fase correspondiente a la transformación de una parte del agua líquida en
hielo. Como consecuencia de esta inmovilización del agua por formación de cristales de hielo se
produce una disminución de la actividad del agua en fase líquida, es decir, el agua no está
disponible para reacciones químicas, enzimáticas, crecimiento de microorganismos...etc. En
la parte congelada del alimento se produce una detención total (a efectos prácticos) de los
procesos que alteran los alimentos (ralentización de la cinética e inmovilización e incluso
destrucción de los agentes del deterioro) lo que le permite a la congelación conservar los
alimentos durante meses o años. En alimentos vegetales es necesario que antes de ser
congelados alcancen un estado de maduración, para que puedan ser consumidos tras su
descongelación. La calidad de un alimento congelado depende en primer lugar de la calidad
propia del producto, siendo la misión de la congelación preservar esa calidad.
Desde el punto de vista fisiológico, el descenso de temperatura por debajo del punto de
congelación provoca la aparición de núcleos de cristalización en torno a los cuales va
solidificando el agua. El número y distribución de éstos depende de la velocidad de congelación.
Si la velocidad de retirada del calor es lenta, la solidificación de agua tiene lugar en
torno a pocos núcleos que dan origen a cristales de hielo grandes que destruyen en proporción
significativa el tejido del alimento. Puesto que la concentración de solutos es menor en los
líquidos intersticiales (entre células) que en el interior del citoplasma, la nucleación comienza y
se extiende en estos espacios, acarreando la destrucción de células, el vaciado del citoplasma y,
lo que es peor, la sucesiva concentración de fluidos en los solutos que contienen (por ir
congelándose el disolvente y tener tiempo de migrar hacia los núcleos) lo que puede dar lugar a
zonas del alimento que no llegan a congelarse nunca.
Cuando la velocidad de retirada del calor es los suficientemente rápida, la velocidad
de nucleación aumenta ya que la masa llega a sobreenfriarse y congelarse simultáneamente en
muchas partes. En este caso la solidificación se produce entorno a muchos microcristales que
resultan inofensivos para la integridad de los tejidos y permiten preservar la textura de muchos
alimentos que de otra forman resultan gravemente dañados.
ULTRACONGELACIÓN: El término ultracongelado se aplica a aquellos productos
que han sido congelados a la mayor rapidez posible. Algunos autores definen ultracongelación
como aquel proceso que consigue una tasa de bajada de temperatura de 5ºC por minuto en el
centro del alimento (punto crítico del alimento) y se prolonga hasta –18ºC. Posteriormente los
alimentos son almacenados a una temperatura inferior a –18ºC.
Estas condiciones de congelación aseguran una calidad óptima del alimento por los
motivos expuestos en el apartado anterior en el que se explican las ventajas de la congelación
rápida. Muchos alimentos solo pueden ultracongelarse si se quiere que después se puedan
consumir.
En cualquier caso siempre hay que tener en cuenta que, incluso a temperaturas de
conservación por debajo de -18ºC, puede llegar a permanecer en estado líquido hasta el 20% del
agua contenida en el alimento debido a la concentración selectiva de solutos causada por la
migración de componentes y a que estos se llegan a concentrar tanto que su punto de
congelación disminuye por debajo de la temperatura mínima de conservación de la cadena del
frio que es de -18ºC (ej: los congeladores domésticos de 4 estrellas alcanzan un mínimo de 24ºC y pueden acercarse a -30ºC en buenas condiciones de operación).
CRIOCONGELACIÓN:
4 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Técnicamente se habla de criocongelación cuando la transferencia del calor se realiza
directamente entre el alimento y un fluido refrigerante. El fluído puede ceder sol calor sensible,
como las salmueras, o latente, como los freones, el nitrógeno o el CO2.
La criocongelación consigue una calidad excepcional de congelación debido tanto al
incremento de la transferencia del calor (al ponerse en contacto con un líquido a veces en
ebullición) como a la mayor diferencia de temperaturas entre el líquido criogénico y el alimento.
Fluidos típicos usados en criocongelación son los freones, que consiguen temperaturas
de entre -20 y -35ºC, CO2, que congela a -78.5ºC y el N2 líquido, que alcanza -195ºC
proporcionando una congelación casi instantanea de gran calidad y muy ventajosa en alimentos
de proporciones reducidas y bajo contenido en agua como pizzas, etc.
En la operación económica de criocongeladores con fluidos no recuperables, es esencial
el aprovechamiento del calor sensible de los gases criogénicos para el preenfriamiento de la
corriente de proceso.
La criocongelación también se aplica en sistemas mixtos, como en la congelación de
frutas de baja resistencia mecánica como fresas, arandanos y otras frutas del bosque, en las que
una primera exposición a un fluido criogénico cra una contras exterior dura congelada que
protege al interior del fruto en durante el resto del proceso en un congelador de tunel tradicional.
Los principales grupos de alimentos congelados industrialmente son:
2
•
Frutas enteras o en forma de puré o zumo,
•
Verduras
•
Pescados y mariscos
•
Carne
•
Alimentos horneados (pan, pasteles),
•
Platos preparados (pizzas, postres, helados).
Cinética del proceso de congelación
Como ya se ha comentado, (y como ya ha visto vd. en otras asignaturas) el problema
fundamental que tiene lugar durante la congelación es una transferencia del calor por
conducción en el estado no estacionario que transcurre con un cambio de fase. En algunos
dispositivos de congelación hay que tener también en cuenta la resistencia a la transferencia del
calor provocada por el medio externo que a menudo tiene lugar por convección.
Por tanto, en un punto dado del interior de un alimento sometido a una temperatura
externa por debajo de su punto de congelación, primero se produce un descenso de temperatura
al perderse calor sensible. Una vez alcanzada la temperatura del punto de congelación, se pierde
calor latente mientras se solidifica el agua, proceso que ocurre sin cambio de temperatura.
Finalmente, una vez congelado el alimento, se sigue perdiendo calor hasta que la temperatura
interna se iguala a la externa.
Según lo descrito, el proceso de congelación puede describirse mediante tres etapas
ideales que se presentan a continuación (ver figura):
5 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Preenfriamiento: Es la etapa que va desde la Ti (temperatura inicial) hasta la Tc (Tª de
congelación), siendo tp el tiempo que tarda el alimento en pasar desde Ti a Tc
Congelación propiamente dicha, el alimento permanece a Tc constante el alimento en su
centro térmico. Siendo tc el tiempo en el que tiene lugar el cambio de fase con lo que varían las
propiedades físicas del alimento durante el transcurso del proceso.
Atemperado o enfriamiento: desde Tc hasta Ta. Siendo ta el tiempo necesario para que
la temperatura del alimento pase desde Tc a Ta.
(Habitualmente todos estos cambios se refieren a lo que pasa en el centro del alimento)
Ti
preenfriamiento
congelación
atemperado
Tc
Ta
tp
Posición
tc
ta
Ti
Ti
Ti
Ti
Tc
Ta
Tc
Ta
Tc
Ta
Tc
Ta
To
tiempo = 0 min
Posición
To
Posición
preefriamiento
To
congelación
Posición
To
atemperado
tiempo
Secuencia de congelación de un alimento (zona sombreada indica congelación)
Diseñar un proceso de congelación consiste en determinar el tiempo que hay que
exponer un determinado alimento a una temperatura dada para que transcurran las tres etapas
descritas. Este es un proceso muy complejo y las tres etapas descritas normalmente coexisten en
el tiempo. Por ejemplo, el centro puede no haber empezado a congelarse cuando la superficie
puede estar ya no solo congelada sino muy cerca de la temperatura de atemperado (incluso por
debajo).
Como el fenómeno es muy complejo, a menudo se usa una descripción simplificada:
suponer que lo que ocurre en el centro es lo que está ocurriendo en todo el alimento. La
situación real y la simplificación habitualmente aceptada se muestran en el siguiente esquema.
6 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Proceso de congelación real
1
2
3
4
5
6
7
8
9
10
Tª Inicial
Punto congelacion, líquido
Tª final requerida
Fresco
Punto congelación, sólido
Bajo Tª final requerida
Frio
Bajo P. congelación
Tª del congelador
Proceso de congelación simplificado
a)
b)
Preenfriamiento
c)
Congelación
d)
Atemperado
Para el diseño de un proceso de congelación prestamos atención a lo que pasa en el
centro térmico del alimento, que es de donde más tarda en evacuarse el calor. De esta forma nos
aseguramos que toda la masa del alimento alcanza la temperatura final requerida, aunque
estemos sobredimensionando el cálculo.
2.1
Descripción rigurosa del problema y simplificaciones aceptadas
La descripción rigurosa y completa del proceso de congelación es muy compleja
(conocer en cada punto y en cada momento la temperatura). Como ya se ha dicho es una
transmisión de calor por conducción en estado no estacionario con cambio de fase. Para resolver
el problema rigurosamente hay que usar la ecuación completa del transporte de calor por
conducción en tres dimensiones teniendo es cuenta el calor latente de congelación como un
7 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
término generación. Es la mayoría de los casos es necesario además tener en cuenta que el calor
es retirado del exterior del alimento por convección.
Este complicado problema sólo se puede resolver programando un método de elementos
finitos en la geometría precisa del alimento. Si bien esto es posible, a menudo resulta demasiado
engorroso y el cálculo se simplifica, recurriendo a una “estimación” conservativa del tiempo de
congelación requerido. Tal simplificación consiste en considerar que vamos a congelar el centro
del alimento y a llevarlo a la temperatura de almacenamiento.
Esta simplificación es muy conservativa porque:
•
La mayor parte del alimento acaba más fría de lo previsto (comparar el estadio
6 en la congelación real con el estadio d en la simplificación)
•
Cuando el centro alcanza el punto de congelación (b), parte del alimento ya está
congelado y por debajo del punto de congelación.
•
Para que el centro se haya congelado, el resto del alimento tiene que estar por
debajo del punto de congelación.
Por tanto, se sobreestiman tanto los descensos de temperatura como los tiempos
empleados en cada paso.
Cuestión: Plantee el cálculo riguroso para una lámina semiinfinita sin resistencia externa a la
transmisión del calor.
Aceptando la simplificación, el tiempo total de congelación viene dado por la suma del
los tiempos invertidos en cada etapa:
tt = tp + tc + ta
Veamos como se calcula cada uno de estos tiempos.
2.2
Determinación de los tiempos de preenfriamiento y atemperado.
Puesto que durante estas etapas no hay cambio de fase, y atendiendo a la simplificación
propuesta en la figura anterior, preenfriamiento y atemperado son dos procesos de enfriamiento
en el estado no estacionario que se pueden resolver usando las gráficas de Gurney y XXX,
siempre que la geometría lo permita. Si no, siempre se puede escoger una geometría
conservativa (más desfavorable que la real a la transferencia del calor, con lo que se vuelve a
sobreestimar el tiempo).
Durante el proceso de preenfriamiento la temperatura del alimento variara con el
tiempo y con la posición desde Ti (inicial) a Tc (congelación). Vamos a encontrar el tiempo
necesario para que el centro alcance Tc.
Como recordará, las soluciones a este caso aparecer en función de los conocidos
módulos adimensionales mostrados en la tabla que aparece a continuación y aproximación
fraccional a la temperatura Y.
Y = fn (Fo, Bi, x )
A modo de recuerdo, la definición de estos módulos es:
8 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Tc − T0
Ti − T0
Y=
Fo =
αl ⋅ t p
x1
Número de Fourier
2
m=
kl
1
=
Bi h ⋅ x 1
n=
x
x1
Inversa del número de Biot
Nº adimensional de posición
y,
αl =
kl
ρ l ⋅ Cp l
Coeficiente de difusividad el alimento en estado líquido
siendo
H
coeficiente de transmisión de calor del medio refrigerante
kl
conductividad térmica del alimento en estado líquido o no congelado
Cpl
calor específico en estado líquido
ρl
densidad del alimento en estado líquido
x1
la distancia al centro térmico desde la superficie del alimento, ejemplo:
lamina L/2 (frente de congelación por ambos lados de la lámina) y L (frente de
congelación por un sólo lado), esfera R, cilindro R.
conocido Y, m y n ⎯grafico
⎯⎯→ Fo ⎯
⎯→ tp
El número de Biot relaciona la resistencia a la transmisión del calor por conducción en
el seno del alimento y la resistencia del medio externo
Bi =
h ⋅ x 1 resistencia interna
=
k1
resistencia externa
La única particularidad en el caso de la congelación es que forman parte de la
resistencia externa la convección del refrigerante (1/h) y la de cualquier recubrimiento o
envoltorio que lleve el alimento (ei/ki).
Así, para un alimento con un recubrimiento de espesor e, el Biot se escribe:
x1
Bi =
k1
resistencia interna
=
1 + e
resistencia externa
h
ke
El resto del problema ya lo ha resuelto vd. muchas veces en esta y en otras asignaturas.
Una vez elegida la geometría y con la solución gráfica pertinente a mano se procede así:
9 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
conocido Y, m y n ⎯grafico
⎯⎯→ Fo ⎯
⎯→ tp
El proceso de atemperado se calcula de forma análoga, suponiendo que pasamos de la
simplificación c) a la d) ver figura. Por tanto, calcularemos el tiempo que tarda el centro en
pasar desde Tc a Ta. Nótese que se acepta que al comenzar el atemperado todo el alimento se
encuentra a la temperatura de congelación. Igual que en el caso anterior:
Y = fn (Fo, Bi, x )
Sólo hay que ser cuidadoso en utilizar las propiedades físicas del alimento congelado:
αc =
kc
ρ c ⋅ Cp c
Coeficiente de difusividad en el alimento congelado
kc
conductividad térmica del alimento en estado congelado
Cpc
calor específico del alimento en estado congelado
ρc
densidad del alimento en estado líquido
x1
la distancia al centro térmico desde la superficie del alimento
Nota: Recuerde que para geometrías finitas (cilindro finito, barras yparalelepípedos)
debe utilizar las formulas de Newman
Para un cilindro finito de diámetro D y altura h:
Y = Ycilindro infinito (D) ⋅ Ylamina infinita (h)
-
Para una barra infinita de sección rectangular (a × b)
Y = Y´lámina infinita (a) ⋅ Ylamina infinita (b)
-
Paralelepípedo (a ×b × c)
Y = Y´lámina infinita (a) ⋅ Ylamina infinita (b) ⋅ Ylamina infinita (c)
2.3
Determinación del tiempo de congelación en geometría plana
Determinar el tiempo de congelación del alimento resulta más complejo puesto que
tiene lugar un cambio de estado que conlleva un cambio en las propiedades físicas del alimento.
Para estimar el tiempo de congelación se acepta como simplificación que todo el cuerpo está en
el punto de congelación (situación b) y que el frente de congelación avanza al irse volviendo el
agua sólida gracias al calor que va escapando por la parte de alimento ya congelada. Se han
propuesto dos soluciones a este problema, una más rigurosa dada por Newman y otra
aproximada propuesta por Plank.
Veamos ambas soluciones aplicadas a una lámina semiinfinita de alimento (frente
plano) y luego las extenderemos a otras geometrías.
2.3.1
Solución rigurosa de Newman
Ambas soluciones son un balance de calor que da la velocidad de avance del frente en
función del calor que sale a través de la capa de alimento congelado. Puesto que la temperatura
10 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
de la capa congelada desciende, la conducción del calor a través de la capa congelada es un
proceso en estado no estacionario, y la ecuación que lo describe es
⎛ ∂ 2T ⎞
⎛ ∂T ⎞
k
=
⎟
c⎜
⎜ ∂x 2 ⎟⎟
⎝ ∂t ⎠
⎠
⎝
ρ c ⋅ Cp c ⎜
(Para h -> infinito, hipótesis de contacto térmico perfecto)
La propuesta de Newman consiste en integrar para ambas fases la ecuación de
transmisión del calor en sólidos en régimen no estacionario. Con las siguientes condiciones de
contorno:
T
b
Condiciones de contorno:
Avance del frente
Para t=0
T(x)=Tc (en todo el cuerpo)
Tc
b=L
Para t>0
Text
x
T=Text en las supeficies
T=Tc en x=<b y en x=>-b
L
-L
0
L
Para la geometría y condiciones iniciales propuestas es posible realizar la integración en
función de Fo, Ko, expresando la temperatura como Y, la posición como y=x/L el avance del
frente como β=b/L. La ecuación que describe el proceso y las condiciones de contorno quedan
⎛ ∂Y ⎞
⎛ ∂β ⎞
⎟⎟ = Ko⎜
⎜⎜
⎟
⎝ ∂Fo ⎠
⎝ ∂y ⎠ b
Fo=0
β=1
Y=1
Fo>0
Y=0
y=1
Y=1
y=β
Donde Ko es un módulo adimensional definido como K o =
(− λ )
Cp c ⋅ (Tc − To )
denominado módulo de Kossovitch.
Las soluciones son de la forma f((Ko, Fo, b)=0, y se puede integrar para diversas
posiciones del frente. Cuando se ha congelado hasta el centro, que es el momento que más nos
interesa, se cumple que β=0 y la solución es
⎛ π ⎞
⎜
⎟
⎝ 4 ⋅ Fo ⎠
1/ 2
⎛ 1 ⎞ 1
⎛ 1 ⎞
⋅ exp⎜
⎟⎟ −
=0
⎟ ⋅ fer ⎜⎜
⎝ 4 ⋅ Fo ⎠
⎝ 4 ⋅ Fo ⎠ Ko
(La función error, fer(), ya la conoce vd del tema de escaldado y pelado al vapor).
Imponiendo Ko se puede despejar Fo y de ahí tc. Es mas sencillo haciendo uso de la
siguiente tabla o de la correspondiente gráfica.
Fo
Ko
Fo
Ko
Fo
11 de 31
Ko
Fo
Ko
Tema 9: Congelación
4º Ingeniero Químico
Fo
100
25
11.1
6.25
4
Ko
199.7
49.67
21.89
12.17
7.67
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Fo
2.78
2.04
1.56
1.24
1.0
Ko
5.23
3.76
2.81
2.15
1.69
Fo
0.83
0.69
0.59
0.51
0.44
Ko
1.35
1.09
0.89
0.73
0.60
Fo
0.39
0.35
0.28
0.25
Ko
0.50
0.42
0.29
0.25
Para Ko>6 se puede aceptar que Fo=Ko/2
2.3.2
Solución aproximada de Plank
Plank propuso aceptar que el perfil de temperaturas en la parte congelada del alimento
corresponde con el de estado estacionario. Esto se acerca bastante a la realidad ya que el frente
avanza muy lentamente.
Resolvamos el caso con esta hipótesis para una lámina plana con contacto térmico
perfecto (Bi>40). Bajo estos presupuestos el perfil de temperaturas en la parte congelada es
lineal, como muestra la figura:
(Cuidado con el pequeño cambio de coordenadas respecto al caso anterior)
T
Capa diferencial
congelandose
Centro (δe)
Avance del frente
Tc
Calor
que
escapa
Text
e
x
0
L
El cálculo del tiempo de congelación se basa en el siguiente balance de energía
Salida = - Generación
⎛ calor invertido ⎞
⎟
⎛ calor perdido ⎞ ⎜
⎜⎜
⎟⎟ = ⎜ en aumentar el frente ⎟
⎝ por conducción ⎠ ⎜ de congelación ⎟
⎝
⎠
12 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Puesto que no hay resistencia externa, la temperatura en x=0 (cara externa) es la del
congelador (To). Calculando la densidad de flujo de calor con la ley de Fourier y el calor latente
cedido en función del diferencial de masa congelado por unidad de area (dm=ρ·dV=ρ·A·dx)
q=
d e(t )
Tc − To
= (− λ ) ⋅ ρ c ⋅ A ⋅
e(t )
dt
kc ⋅ A
Donde e(t( es el grosor de la capa congelada, que aumenta con el tiempo y
d e(t )
es la
dt
velocidad de congelación. Integrando:
d e(t )
Tc − To
⋅ k c ⋅ A = (− λ ) ⋅ ρ c ⋅ A ⋅
e(t )
dt
Integrando obtenemos,
t
∫ dt =
0
(− λ ) ⋅ ρ c e
e(t ) ⋅ de(t )
(Tc − To ) ⋅ k c ∫0
Y de aquí:
t=
(− λ ) ⋅ ρ c e 2
⋅
(Tc − To ) ⋅ k c 2
Cuando e=L se ha completado el proceso de congelación y de ahí se obtiene el tiempo.
tc =
(− λ ) ⋅ ρ c ⋅ L2
(Tc − To ) ⋅ k c 2
Agrupando en función de los números adimensionales, que tan cómodos resultan,
queda:
Fo =
Ko
2
(Pruebe a reordenarla vd.)
Que coincide con el resultado de Newman cuando Ko>6.
Si el frente de congelación es doble, L es el semiespesor del alimento a congelar. Si sólo
hay un frente de congelación, L es el espesor completo.
2.4
Estimación de la velocidad de congelación
El desarrollo de la hipótesis de Plank permite obtener una expresión aproximada para la
velocidad de congelación v(t) en geometría plana que puede ser utilizada para estimar la calidad
del proceso. Como antes ya se ha mencionado
v=
d e(t ) (Tc − To) ⋅ k c
=
(− λ ) ⋅ ρ c ⋅ e(t )
dt
13 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Que da la velocidad de congelación en función del avance del frente. De aquí sale la
velocidad mínima cuando e=L.
v min =
(Tc − To) ⋅ k c
(− λ ) ⋅ ρ c ⋅ L
La velocidad de congelación también se puede poner en función del tiempo de
congelación . Puesto que
(− λ ) ⋅ ρ c e 2
t=
⋅
(Tc − To ) ⋅ k c 2
, se puede despejar el avance del frente
2 ⋅ (Tc − To ) ⋅ k c ⋅ t
. Sustituyendo en la expresión de la velocidad
(− λ ) ⋅ ρ c
e(t ) =
v=
(Tc − To) ⋅ k c
(− λ ) ⋅ ρ c ⋅
2 ⋅ (Tc − To ) ⋅ k c ⋅ t
(− λ ) ⋅ ρ c
=
1
2 ⋅ (− λ ) ⋅ ρ c ⋅ t
(Tc − To) ⋅ k c
=
(Tc − To) ⋅ k c
2 ⋅ (− λ ) ⋅ ρ c ⋅ t
Y queda puesta en función del tiempo
v=
(Tc − To) ⋅ k c
2 ⋅ (− λ ) ⋅ ρ c ⋅ t
La velocidad mínima tiene lugar al final del proceso de congelación, cuando t=tc. Es
decir
v min =
(Tc − To) ⋅ k c
2 ⋅ (− λ ) ⋅ ρ c ⋅ tc
Estas expresiones permiten resolver problemas tales como calcular la temperatura
necesaria en el congelador para conseguir una determinada velocidad mínima de congelación o
el máximo grosor admisible.
2.5
Influencia de la resistencia térmica externa en el tiempo de congelación.
El tratamiento propuesto por Plank permite extender la estimación del tiempo de
congelación a situaciones en las que la resistencia externa tiene importancia, lo que se pone de
manifiesto porque Bi<40.
En este caso, el calor que escapa por conducción tiene que atravesar además la
resistencia del medio externo. La superficie externa del alimento está, en este caso, a una
temperatura que denominaremos Ts que es superior a la temperatura del congelador, To
(recuerde que Tc es la temperatura de congelación del alimento). El balance de calor ahora es:
calor invertido
⎛
calor perdido por
calor perdido por
⎛
⎞ ⎛
⎞ ⎜
⎜⎜
⎟⎟ = ⎜⎜
⎟⎟ = ⎜ en aumentar el grosor de
⎝ conducción a traves del frente ⎠ ⎝ convección a traves del fluido ⎠ ⎜
la capa congelada
⎝
Q=
kc
d e(t )
⋅ A ⋅ (Tc − Ts ) = h ⋅ A ⋅ (Tc − To ) = (− λ ) ⋅ ρ c ⋅ A ⋅
e(t )
dt
Que se puede reordenar para agrupar las resistencias según:
14 de 31
⎞
⎟
⎟
⎟
⎠
Tema 9: Congelación
4º Ingeniero Químico
Q=
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
d e(t )
Tc − To
= (− λ ) ⋅ ρ c ⋅ A ⋅
1
e(t )
dt
+
kc ⋅ A h ⋅ A
Observe que con esto la transferencia del calor ha quedado en función de la fuerza
impulsora global del proceso (Tc-To), que sí podemos calcular y es constante durante todo el
proceso. Separamos variables para integrar la ecuación.
dt =
(− λ ) ⋅ ρ c ⎛⎜ e(t ) 1 ⎞⎟
⋅ d e(t )
⋅
+
(Tc − To ) ⎜⎝ k c h ⎟⎠
De esta ecuación han DESAPARECIDO las AREAS, A, al simplificar porque EN LA
GEOMETRÍA PLANA LA SECCIÓN DE PASO DEL CALOR ES CONSTANTE. Ahora se
puede integrar la ecuación.
(− λ ) ⋅ ρ c 1
1
∫0 dt = Tc − To ⋅ k c ∫0 e(t ) ⋅ d e(t ) + Tc − To ⋅ h ∫0 d e(t )
tc
tc =
(− λ ) ⋅ ρ c
(− λ ) ⋅ ρ c
L
L
1 L2 (− λ ) ⋅ ρ c 1
⋅
+
⋅ ⋅L
Tc − To k c 2
Tc − To h
⋅
Expresión que permite estimar el tiempo de congelación cuando la resistencia externa es
significativa. Reordenando en función de los módulos adimensionales que venimos usando
queda:
Fo 1 1
= +
Ko 2 Bi
Dese cuenta que la resistencia externa puede venir dada por un recubrimiento, y no
tiene por qué ser causada exclusivamente por una convección pobre. Por ejemplo, si el alimento
estuviese recubierto por un plástico de espesor er y conductividad kr su resistencia vendía dada
por er/kr y aparecería en vez del término 1/h de la ecuación integrada.
Si ambos factores existiesen a la vez, convección pobre y recubrimiento, ambas
resistencias externas se sumarian:
(resistencia externa) = 1/h + er/kr
Pudiendo ponerse tantos términos como haga falta. Si lo revisa, notará vd que lo que se
acaba de exponer ya está recogido en la definición del Biot expuesta en la página 9 (que
x1
repetimos por comodidad) Bi =
k1
resistencia interna
=
1 + e
resistencia externa
h
ke
Lo más conveniente y fácil de recordar es la ecuación en su forma adimensional y esta
definición del Biot que es la que se usa en los siguientes apartados.
2.6
Estimación del tiempo de congelación en otras geometrías.
Para estimar el tc en geometrías diferentes de la plana, como por ejemplo la cilíndrica
semiinfinita (espárrago), la esférica (patata) o un paralelepídedo (patata frita), basta realizar el
mismo balance de calor que aparece al principio del apartado 2.5.
15 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
En estos casos aparece una dificultad adicional: el área de paso del calor A, no es
constante. El área externa y la del frente de congelación ya no son equivalentes. El área del
frente disminuye de forma inversamente proporcional al espesor congelado en la geometría
cilíndrica e inversamente proporcional al cuadrado del espesor congelado en la geometría
cilíndrica. Esto tiene dos efectos en la ecuación diferencial del balance de energía.
•
En primer lugar, el diferencial de masa congelada ρ·A·de/dt se calcula de forma
diferente ya que A no es una constante, sino que disminuye durante el proceso
(generalmente).
•
Además, para aplicar la Ley de Fourier hay que calcular un área media entre la
externa y la del frente. El tipo de media depende la geometría.
Por ejemplo, en geometría cilíndrica semiinfinita (cilindro infinito de radio R) siendo e
el espesor congelado, el área del frente es función de e según la expresión:
A(e) = 2 ⋅ π ⋅ r ⋅ H = 2 ⋅ π ⋅ ( R − e) ⋅ H = 2 ⋅ π ⋅ ( R − e)
(Para la unidad de longitud de cilindro, H=1)
Y el área a usar en geometría cilíndrica para calcular la extracción de calor a través del
espesor congelado es la media logarítmica, Aml, entre el área externa, Aext, y la que presenta el
frente en cada momento A(e). Es decir:
Aml =
Aext − A(e)
2 ⋅ π ⋅ R − 2 ⋅ π ⋅ ( R − e)
e
=
= 2 ⋅π ⋅
ln ( Aext / A(e) ) ln (2 ⋅ π ⋅ R / 2 ⋅ π ⋅ ( R − e) )
ln (R /( R − e) )
(Ya expresado por unidad de longitud)
Para la geometría esférica, esta área se corresponde con la media geométrica. Para una
geometría general, el tipo de media que representa al área se puede deducir de las siguientes
consideraciones: el calor que re transfiere entre dos superficies isotermas muy próximas es, en
cada punto es
Q = k c ⋅ A( x) ⋅
espesor
e
Q⋅∫
0
de
frente
dT
, donde x representa a cualquier punto entre la superficie y el
dx
congelado,
e.
Despejando
e
integrando
se
obtiene
Ts
dx
= k c ⋅ dT = k c ⋅ (Tc − Ts ) , y comparando con la ecuación de Fourier se deduce
A( x) Tc∫
que la superficie media a emplear en el balance de energía es
Am =
e
∫
0
e
dx
A( x)
donde A(x) es la expresión que da el área de la superficie isoterma situada en cualquier
punto entre la superficie externa y el frente de congelación.
Si se introducen estas modificaciones en el balance de energía, resulta una ecuación
difícil de integrar. Veámosla
Q=
kc
de
⋅ Am ⋅ (Tc − Ts ) = h ⋅ A ⋅ ext (Tc − To ) = (− λ ) ⋅ ρ c ⋅ A(e) ⋅
e
dt
Que se puede reordenar a:
16 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Tc − To
e
1
+
k c ⋅ Am h ⋅ Aext
= (− λ ) ⋅ ρ c ⋅ A(e) ⋅
de
dt
Reordenando e integrando
L
⎛ A(e) ⋅ e k c ⋅ A(e) ⎞
k c ⋅ (Tc − To)
⋅
=
dt
∫0 (− λ ) ⋅ ρ c
∫0 ⎜⎜⎝ Am + h ⋅ Aext ⋅ ⎟⎟⎠d e
tc
Que en función de la difusividad térmica, α, y el Ko, queda:
α c ⋅ tc
Ko
L
k ⋅ A(e)
A(e) ⋅ e
⋅d e+ ∫ c
⋅d e
Am
h ⋅ Aext
0
L
=∫
0
Dividiendo por L2 en ambos términos
α c ⋅ tc
Ko ⋅ L2
L
=∫
Fo 1
=
Ko L2
0
L
∫
0
L
L
k c ⋅ A(e)
kc
A(e) ⋅ e
A(e) ⋅ e
⋅d e+ ∫
⋅d e = ∫
⋅d e+
2
2
2
Am ⋅ L
h ⋅ Aext ⋅ L2
0 h ⋅ Aext ⋅ L
0 Am ⋅ L
L
∫ A(e) ⋅ d e
0
L
kc ⋅V
kc ⎞
A(e) ⋅ e
V ⎛ Aext A(e) ⋅ e
⎜
⎟
⋅
+
d
e
⋅d e+
=
Am
h ⋅ L ⎟⎠
h ⋅ Aext ⋅ L2 Aext ⋅ L ⎜⎝ V ⋅ L ∫0 Am
Definiendo D =
V
Aext ⋅ L
yG=
Volumen
congelado
⎛ e dx ⎞
Aext L
⎜∫
⎟
⋅
A
e
(
)
⎜ A( x) ⎟de
V ⋅ L ∫0
0
⎝
⎠
Finalmente queda
Fo
⎛ 1
⎞
= D⋅⎜ + G⎟
Ko
⎝ Bi
⎠
D y G son dos números que dependen sólo de la geometría.
D puede calcularse siempre con cierta facilidad pero G da más dificultades y a menudo
ha de calcularse numéricamente. En geometrías muy irregulares o sin simetrías puede ser difícil
o imposible determinas las superficies isotermas y con ello A(x) y han de aproximarse por otras
geometrías.
Por ejemplo para una varilla de longitud infinita y sección transversal rectangular de
dimensiones 2L×2EL (siendo L el semiespesor del lado más delgado, suponiendo que el frente
avanza por todos lados y E la proporción entre el lado más grueso y el más delgado), D se
calcularía mediante la siguiente ecuación:
D=
2⋅E
2⋅E + 2
Otro ejemplo, para un paralelepípedo recto (ladrillo) de dimensiones 2L×2E1L×2E2L,
donde L representa el semiespesor del lado más delgado y E1 y E2 son factores de
proporcionalidad entre 2L y las otras dimensiones, D se calcula mediante la ecuación:
D=
E1 ⋅ E 2
E1 + E 2 + E1 ⋅ E 2
G puede encontrarse en bibliografía para una amplia gama de circunstancias. Como
ejemplo podría integrar vd G para el cilindro semiinfinito.
17 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
A(e) = 2 ⋅ π ⋅ ( R − e)
G=
R
⎛e
⎞
⎛ e dx ⎞
Aext L
dx
2 ⋅π ⋅ R ⋅ L
⎜
⎟
⎜∫
⎟
⋅
⋅
−
⋅
=
−
⋅
R
e
de
R
e
π
2
(
)
(
)
2
2 ∫
⎜ ∫ 2 ⋅ π ⋅ ( R − x) ⎟
⎜ ( R − x) ⎟de
V ⋅ L ∫0
⋅
⋅
R
L
ρ
0
⎝0
⎠
⎝0
⎠
(Acabe usted)
G se encuentra tabulado en bibliografía para las geometrías más comunes: cilíndrica,
esférica, varilla semiinfinita y “ladrillo” (estos dos últimos en función de E ó de E1 y E2
respectivamente).
A modo de resumen muy simplificado, se puede usar la siguiente tabla para D y G
Geometría
Lámina
Cilindro
Esfera, Cubo
2.7
G
0,5
0,5
0,5
D
1,0
0,5
0,33
Estimación del tiempo total de congelación. Otros métodos.
Una vez estimado el tiempo de preenfriamiento y atemperado mediante las graficas de
transmisión del calor en estado no estacionario y, por ejemplo, la solución aproximada de Plank,
el tiempo total de congelación se estima como la suma de estas tres contribuciones.
Se puede decir que el único tiempo evaluado con cierta precisión es el preefriamiento
(tp) ya que es el único en el que los supuestos bajo los que se hace el cálculo se acercan a la
realidad.
Aunque la solución de Plank subestima el tiempo de congelación, en realidad resulta
sobreestimado ya que en la realidad cuando termina el preenfriamiento ha comenzado la
congelación del exterior y se lleva cierto tiempo “ganado”.
Finalmente, el atemperado está muy sobreestimado por razones obvias.
En general no conviene precisar más porque los alimentos son sustancias muy
heterogéneas y es difícil precisar en sus propiedades.
Se han propuesto algunas ecuaciones empíricas para estimar los tiempos de estos
periodos o para corregir los tiempos dados por la solución de Plank. Entre éstas cabe citar las
ecuaciones de Nagaoka y colaboradores o Cleland & Earle para el tiempo de congelación y la de
Rutox para el atemperado. Estas ecuaciones y su aplicabilidad se discutirán brevemente en
clase.
3
Propiedades térmicas de los alimentos.
Para calcular el tiempo de los diversos periodos de congelación, es necesario conocer
las propiedades térmicas que ya ha tenido vd oportunidad de ver en el desarrollo de los
apartados anteriores.
En bibliografía (Food Properties Handbook, 1995, Rahman), se encuentran tabuladas un
gran número datos físicos y químicos de diferentes alimentos, necesarios para el diseño de los
aparatos de congelación. También se han facilitado datos en el Tema 4 de esta misma
asignatura.
18 de 31
Tema 9: Congelación
4º Ingeniero Químico
3.1
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Calor latente de congelación, capacidad calorífica de los alimentos y conductividad
térmica.
Si no se dispone de otra cosa, los calores específicos y latentes de un alimento se
pueden estimar aproximadamente a partir de la fracción másica de agua, xA en el alimento
mediante las ecuaciones propuestas por Woolrich y Siebel.
λ= 80 × xA (kcal/kg)
Cpl= 0,80 × xA + 0,20 (kcal/ kg·°C)
Cpc= 0,30 × xA + 0,20 (kcal/ kg·°C)
Debe tenerse cuidado porque estas ecuaciones son indicadas para alimentos con elevado
contenido en agua, que por otra parte forman la mayoría de los que se congelan (carne, pescado,
verduras, frutas, hortalizas, pan y platos preparados).
3.2
Temperatura del punto de congelación
El punto de congelación es otro dato fundamental para realizar el cálculo del tiempo de
congelación total. De hecho, es el único dato físico necesario para los tres periodos que
componen el tiempo total de la operación de congelación.
Determinar la temperatura de congelación de un alimento no es tan sencillo como puede
parecer por dos motivos principales:
•
El punto de congelación depende del contenido en solutos de agua y este puede
variar de un alimento a otro, en diferentes puntos del mismo.
•
El punto de congelación puede variar durante el proceso de congelación, al
producirse elevaciones locales de la concentración de los solutos (congelación
segregada).
Esto ocurre en todos los alimentos en mayor o menor grado. Por eso la congelación
propiamente dicha acaba produciéndose en un intervalo de temperaturas en el que coexisten
diferentes proporciones de agua sólida y líquida. En muchos alimentos siempre queda una
cantidad sustancial de agua líquida, incluso a la temperatura de almacenamiento Ta.
¿Cómo definir, por tanto el punto de congelación? Para ello juega un importante papel
la relación (masa de hielo)/(masa de agua) en el alimento y su variación con la temperatura. En
comportamiento típico es que esta relación, que denominaremos A, frente a A experimenta en
un determinado punto una apreciable variación en su tasa de crecimiento (la pendiente de A
frente a T). Esto se muestra en la siguiente gráfica.
A
Tc
Aproximadamente
-2 a –3ºC
T
Ese punto es el que se suele dar como temperatura de congelación, ya que representa el
agua del alimento que se encuentra libre (relativamente) para congelarse, siendo el resto agua
retenida con mayor o menor intensidad.
19 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Tal y como se muestra en la gráfica, el punto de congelación de muchos alimentos
(carnes, pescados, frutas y otros alimentos con elevado contenido en agua) se encuentra entre
los -2 y -3 ºC, como puede vd comprobar en la tabla siguiente.
Especial cuidado hay que tener con los alimentos que contienen sustancias con
actividad osmótica, como salmueras, jarabes o crioprotectores como la glicerina, porque
experimentan descensos muy fuertes en el punto de congelación. Dentro de esta categoría entran
los zumos concentrados y purés de fruta que se congelas con sacarosa como crioprotector
(mantiene una mejor calidad después de congelar y además le da mejor sabor sobre todo a frutas
agrias).
Estimación del punto de congelación:
Si usted dispone de alguna información sobre la concentración en solutos del agua del
alimento y el peso molecular de éstos, podría utilizar las formulas para calcular el descenso
crioscópico que debe conocer de otras asignaturas. Esta situación se da por ejemplo en el caso
de jarabes o salmueras. Por ejemplo congelando frutas en un jarabe de sacarosa al 10%. O
también en sumos concentrados, en los que puede conocerse aproximadamente la composición.
Sin embargo en la mayoría de los casos es necesario remitirse a la bibliografía u obtener
los datos experimentalmente de un experimento como el descrito en la gráfica anterior. La tabla
siguiente muestra la temperatura del punto de congelación de algunos alimentos representativos.
20 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Como norma general podría decirse que a mayor contenido en agua, más alto es el
punto de congelación, aunque es posible encontrar multitud de excepciones aunque con
pequeñas desviaciones.
3.3
Contenido en agua libre de los alimentos congelados
Debe quedar claro que por mucho que se baje la temperatura de un alimento congelado,
siempre queda algo de agua en el estado líquido, bien porque es retenida muy fuertemente por
21 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
algunas moléculas del alimento, bien porque la congelación ha sido segregada y se ha producido
acumulación de solutos en el agua que va quedando sin congelar.
La importancia de conocer la fracción de agua no congelada viene de que loa alimentos
con una baja fracción de agua líquida se conservan mejor. Además, es importante para calcular
la entalpía del alimento congelado con vistas al balance de energía que permite dimensional los
equipos de refrigeración.
Aunque existen algunos métodos teóricos, los alimentos son sustancias complejas y
difíciles de definir, por lo que lo mejor es acudir a la bibliografía u obtener los datos
experimentalmente. En la siguiente tabla vemos algunos ejemplos de alimentos y el contenido
en agua líquida a la temperatura de almacenamiento.
22 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
23 de 31
Tema 9: Congelación
4º Ingeniero Químico
4
4.1
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Aspectos tecnológicos de la congelación
Calidad de los alimentos congelados
La calidad de un alimento congelado depende:
•
De la calidad del alimento antes de ser congelado
•
Del proceso de congelación
En este sentido al proceso se le puede pedir que conserve durante el mayor tiempo
posible las cualidades organolépticas que existen en el alimento, para ello es importante que la
24 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
velocidad de congelación sea lo suficientemente rápida para que atraviese en el menor tiempo
posible el intervalo de temperaturas correspondiente al crecimiento rápido de los
microorganismos (entre 45 y 4ºC). Por debajo de 4ºC sólo se produce el crecimiento lento de
algunos microorganismos psicrofilicos que en un tiempo suficiente pueden deteriorar al
alimento pero sin peligro para la salud.
Sin embargo desde un punto de vista práctico la congelación también debe de ser
rápida, ya que una congelación lenta puede deteriorar al alimento por dos factores:
Efectos de concentración, al irse separando los cristales de agua las disoluciones de los
azucares sales, es decir las sustancias solubles del alimento se encuentran más concentradas y
pueden precipitar desnaturalizando a las proteínas por efecto salino o cambio de pH.
Efecto debido al crecimiento de los cristales de hielo, pues si la congelación es lenta los
cristales formados son grandes y pueden destruir la estructura de los alimentos.
Por estas razones, la congelación debe de ser rápida, admitiéndose que una velocidad de
avance del frente congelación de 1 cm/h o superior es adecuada (Norma DIN 8956, Alemania).
Esta velocidad por ejemplo se podría conseguir en la mayor parte de los alimentos con aire a –
40ºC circulando con una velocidad de 5 m/s sobre la superficie del alimento.
La velocidad de congelación dependerá:
•
Con respecto al alimento: conductividad térmica del alimento (kl) y su tamaño,
cuanto menor sea la distancia del centro térmico a la superficie del alimento en
contacto con el sistema congelante más rápida será la congelación.
•
Con respecto al equipo de congelación: gradiente térmico que crea (To) y su
coeficiente individual de transmisión del calor.
Q (kcal / h ) = h ⋅ A ⋅ (Ts − To)
Por otra parte, la conservación de los alimentos congelados debe de hacerse a una
temperatura tal que las actividades enzimáticas estén completamente paralizadas y que haga
imposible el crecimiento de los cristales de hielo. Si además se tiene en cuenta que, por ejemplo,
en el caso de los peces su actividad vital se desarrolla normalmente a temperaturas próximas a
los 0ºC, se comprende que los alimentos congelados deben almacenarse por debajo de –18ºC,
según establece la AFDOUS (Association of Food and Drug Officials of United States).
4.2
Métodos de congelación y equipos industriales
Los métodos que se utilizan en la práctica para llevar a cabo la refrigeración y la
congelación de alimentos pueden clasificarse en:
4.2.1
•
Congelación por contacto directo
•
Congelación por contacto con un líquido refrigerado
•
Congelación por contacto con un gas refrigerado
•
Congelación por contacto directo con un líquido que se vaporiza.
Congelación por contacto directo: congeladores de placas
Se caracteriza porque el calor se transmite desde el alimento hasta el refrigerante a
través de una pared sólida metálica. Destacan los congeladores de placas, generalmente de
aluminio o cualquier otro metal de elevada conductividad térmica.
25 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Placas huecas
Paquetes de alimentos
Circula el refrigerante
-30ºC a –40ºC
Las placas se montan en paralelo en sentido vertical u horizontal. Los espacios entre las
placas son variables abriéndose para ser cargadas de alimentos envasados o sin envasar y
cerrándose antes de proceder a la congelación. De forma que la superficie de las placas están en
íntimo contacto con el alimento envasado o sin envasar.
Generalmente en los congeladores de placas horizontales se suelen utilizar alimentos
envasados en cajas de cartón con un grosor comprendido entre 4 y 5 cm. En las placas y los
paquetes de alimentos se mantiene una presión moderada entre 0,07 kg/cm2 y 0,3 kg/cm2 para
conseguir un buen contacto.
Este tipo de equipos puede trabajar de forma continua adaptándoles sistemas de carga y
descarga automática.
Los cargadores de placas verticales son muy adecuados para la congelación de
materiales deformables sin envasar del tipo de pescado, carne, etc. Se utilizan principalmente en
la congelación de peces en alta mar.
Para conseguir coeficientes de transmisión de calor elevados y uniformes los envases
deben estar completamente llenos de alimentos y las placas no deben tener ni hielo ni otro tipo
de depósitos (80-160 kcal/h·m2·ºC).
4.2.2
Congelación por contacto con un líquido refrigerado: inmersión
Se consiguen mayores coeficientes de transmisión de calor, del orden de 500
kcal/h·m2·ºC. Se obtienen mayores velocidades de congelación.
26 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
La congelación se realiza sumergiendo el alimento en un líquido refrigerado que debe
de ser no tóxico. Las piezas de alimento se congelan separadas aunque su forma sea irregular, es
decir, se obtienen productos IQF (individually quick frozen).
La dificultad mayor de este sistema de congelación es evitar la contaminación mutua
entre alimentos y líquidos refrigerados. Los líquidos refrigerantes más utilizados son:
•
disoluciones de NaCl 23% en peso de agua. Se puede utilizar hasta –20ºC, su
empleo implica salar alimentos, se utiliza en alta mar para pescados.
•
Disoluciones de azúcar en agua (63% en peso). También alcanza los –20ºC. Por
lo misma razón solo se utiliza para congelar productos dulces, como frutas.
•
Disoluciones de glicerina y de propilenglicol, que permiten alcanzar
temperaturas mucho más bajas. Una disolución acuosa con un 67% en peso de
glicerina congela a –47ºC y del 60% de propilenglicol a –51ºC.
Estas dificultades se eliminan si se utilizan alimentos envasados herméticamente, por
ejemplo latas, en este caso es preferible utilizar líquidos menos viscosos y más volátiles, como
alcohol refrigerado (-112ºC).
4.2.3
Congelación por contacto directo con un gas refrigerado
El gas utilizado es aire o nitrógeno. Es una técnica muy utilizada y hoy día sigue siendo
un proceso rentable. Se utiliza para alimentos irregulares y se obtienen productos IQF.
La contaminación del alimento es escasa pero hay que evitar transferencia de materia
desde el alimento al gas refrigerado, que suele consistir en la evaporación de agua del alimento
(en el caso de productos sin envasar).
El mayor inconveniente de estos congelados es que suministran coeficientes de
transmisión de calor relativamente bajos:
•
Convección natural, 5 kcal/h·m2·ºC
•
Velocidad del aire de 2,5 m/s, 15 kcal/h·m2·ºC
•
Velocidad del aire de 5 m/s, 25 kcal/h·m2·ºC
Los congeladores de aire frío pueden operar continuamente o discontinuamente y suelen
utilizar una velocidad rápida del aire (5-15 m/s) a temperaturas comprendidas entere –25ºC y –
45ºC. Por esta razón se llaman congeladores de ráfaga.
El orden de magnitud del coeficiente de transmisión de calor varía con la velocidad del
aire en la forma
27 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
h α (v )
0 ,8
siendo v la velocidad del gas.
Un congelador de ráfaga de aire está formado por:
•
ventiladores, para provocar el movimiento del aire
•
serpentines de refrigeración para enfriamiento del mismo
•
cámara o zona de contacto entre el alimento y el aire frío.
Esta última cámara suele ser un túnel a través del cual se transporta el alimento en
vagonetas, cinta sinfín o en caso de la carne en ganchos suspendidos. El aire puede fluir en
paralelo o perpendicular a la dirección del movimiento del producto (flujo cruzado).
Dentro de este grupo destacan los congeladores de lecho fluidizado que se caracterizan
porque la cinta sinfín es de malla, fluyendo el aire perpendicularmente. Es muy útil para
productos de pequeño y uniforme tamaño.
Congelador de lecho fluidizado
28 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Congelador de ráfaga de aire.
Congelador de cinta en espiral.
4.2.4
Congeladores por contacto con líquido que se vaporiza: congeladores criogénicos
Los líquidos más utilizados son el N2 y los hidrocarburos halogenados, aunque también
se utilizan sistemas sólidos como el CO2. El efecto refrigerante está proporcionado por el
cambio de fase y por el calor sensible que adsorbe el agente refrigerante, calor que se emplea en
preenfriar el alimento.
Así, por ejemplo el N2 líquido tiene un calor latente de 200 kJ/kg a –196ºC (punto de
ebullición 1 atm) y absorbe otros 209 kJ/kg para elevar su temperatura a -18ºC.
29 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
El agente refrigerante se pulveriza sobre el alimento a una velocidad controlada para
regular la velocidad de congelación y después es evacuado a la atmósfera.
Con este método se han conseguido vegetales congelados con una textura inmejorable y
se ha hecho posible mejorar la calidad de los productos que no se congelan bien por métodos
convencionales (por ejemplo champiñones y productos marinos como mariscos).
El sistema permite disminuir la perdida de peso del producto por evaporación del agua,
dada la pequeña presión de vapor de la misma a esta temperatura.
El coste de la congelación con N2 líquido depende en gran medida del propio N2. Es
más caro que la congelación convencional aunque el precio puede ser compensando por la
mejor calidad del producto.
5
Descongelación
La correcta descongelación de los alimentos también es una técnica muy importante. La
descongelación se considera terminada cuando se alcanza los 0ºC. Aunque la descongelación es
el proceso inverso de la congelación, existen diferencias significativas entre ambas. Aplicando
el mismo gradiente térmico, la descongelación es mucho mas lenta que la congelación por dos
motivos:
La conductividad térmica del hielo es cuatro veces superior a la del agua.
k(hielo): 2,25 W/m·K a 0ºC
k(agua): 0,57 W/m·K a 0ºC
Durante la congelación lo primero que se funde es la capa superficial de hielo del
alimento. Esta capa de agua formada tendrá menor conductividad y difusividad térmica que el
hielo original, reduciéndose notablemente la velocidad de transmisión de calor hacia el interior
del alimento. Este fenómeno se acentúa a medida que transcurre la descongelación.
No se pueden emplear gradientes de temperatura de gran magnitud entre el medio de
calentamiento y el alimento congelado, para evitar el calentamiento excesivo de las capas
externas y el crecimiento de microorganismos.
Durante la descongelación también se aprecian tres etapas claras.
•
1ª etapa llamada atemperado, la temperatura del alimento se eleva rápidamente
porque no hay agua superficial y el hielo actúa como un buen conductor del
calor.
•
2ª etapa es mucho más prolongada y se corresponde con la aproximación de la
temperatura del producto al punto de fusión. En el momento en que comienza la
fusión de la capa superficial del hielo la velocidad de transmisión de calor, y
por lo tanto la descongelación, disminuye notablemente.
•
3ª etapa, una vez que todo el hielo se ha fundido, la temperatura aumenta hasta
igualarse con la del medio caliente.
De la comparación de ambas cinéticas (congelación y descongelación) destaca que la
principal diferencia se encuentra en la segunda etapa en la cinética de descongelación ya que la
fusión se realiza justo por debajo de los 0ºC, lo que favorece la degradación del alimento
(elevada concentración de solutos, se favorece el crecimiento de microorganismos...).
En la descongelación se debe cumplir:
•
Evitar el calentamiento excesivo del producto
•
Reducir al mínimo el tiempo de descongelación
•
Evitar la deshidratación excesiva si se emplea aire.
30 de 31
Tema 9: Congelación
4º Ingeniero Químico
Tecnología de los Alimentos
Dpt. Ingeniería Química - UAL
Bibliografía
Heldman DR, Lund DB (1992) Handbook of food engineering. Marcel Dekker Inc.,
New York.
Karel M, Lund DB (2003) Physical Principles of Food Preservation Marcel Dekker Inc.,
New York. (ISBN: 0824740637)
Filename: F:\JMFS\TA\Tema9\Tema9-Congelacion.doc
Author: Jose Maria Fernandez Sevilla
LastSaved: 05/10/2005 12:28:00
LastPrint: 14/10/2005 13:23:00
NOMBRE
FERNANDEZ
SEVILLA JOSE
MARIA - NIF
27518815M
Firmado digitalmente por NOMBRE
FERNANDEZ SEVILLA JOSE MARIA NIF 27518815M
Nombre de reconocimiento (DN): CN =
NOMBRE FERNANDEZ SEVILLA
JOSE MARIA - NIF 27518815M, C =
ES, O = FNMT, OU = FNMT Clase 2
CA
Motivo: Soy el autor de este documento
Fecha: 2005.10.14 13:33:17 +02'00'
31 de 31