guía

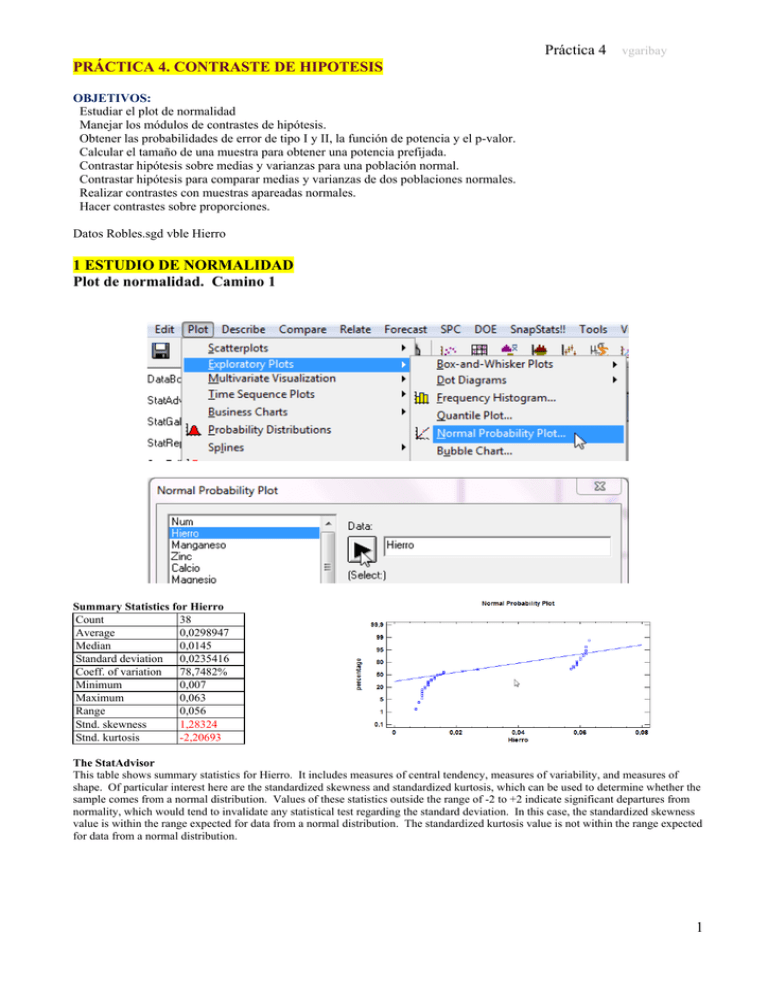
Práctica 4 vgaribay
PRÁCTICA 4. CONTRASTE DE HIPOTESIS
OBJETIVOS:
Estudiar el plot de normalidad
Manejar los módulos de contrastes de hipótesis.
Obtener las probabilidades de error de tipo I y II, la función de potencia y el p-valor.
Calcular el tamaño de una muestra para obtener una potencia prefijada.
Contrastar hipótesis sobre medias y varianzas para una población normal.
Contrastar hipótesis para comparar medias y varianzas de dos poblaciones normales.
Realizar contrastes con muestras apareadas normales.
Hacer contrastes sobre proporciones.
Datos Robles.sgd vble Hierro
1 ESTUDIO DE NORMALIDAD
Plot de normalidad. Camino 1
Summary Statistics for Hierro
Count
38
Average
0,0298947
Median
0,0145
Standard deviation 0,0235416
Coeff. of variation
78,7482%
Minimum
0,007
Maximum
0,063
Range
0,056
Stnd. skewness
1,28324
Stnd. kurtosis
-2,20693
The StatAdvisor
This table shows summary statistics for Hierro. It includes measures of central tendency, measures of variability, and measures of
shape. Of particular interest here are the standardized skewness and standardized kurtosis, which can be used to determine whether the
sample comes from a normal distribution. Values of these statistics outside the range of -2 to +2 indicate significant departures from
normality, which would tend to invalidate any statistical test regarding the standard deviation. In this case, the standardized skewness
value is within the range expected for data from a normal distribution. The standardized kurtosis value is not within the range expected
for data from a normal distribution.
1
Práctica 4 vgaribay
Plot de normalidad. Camino 2
Tests de Ajuste; tests de Normalidad (métodos más precisos)
2
Práctica 4 vgaribay
Hierro
Nitrógeno
3
Práctica 4 vgaribay
2 UNA MUESTRA NORMAL (Describe)
2.1 a partir de datos
DatosContrastes
2.1.a y c) Tests de un lado sobre la media y la dispersión
Tests de Hipótesis > Pane Options
(apartados a y c)
4
Práctica 4 vgaribay
Hypothesis Tests for longitud
Sample mean = 10,035
Sample median = 10,045
Sample standard deviation = 0,173157
t-test
Null hypothesis: mean = 10,0
Alternative: less than
Computed t statistic = 0,639187
P-Value = 0,730686
Do not reject the null hypothesis for alpha = 0,05.
chi-square test
Null hypothesis: sigma = 0,4
Alternative: less than
Computed chi-square statistic = 1,68656
P-Value = 0,0044883
Reject the null hypothesis for alpha = 0,05.
Plot ajuste a la Normal
Complemento: Tests de Ajuste
5
Práctica 4 vgaribay
2.1.b) Test dos lados sobre la media
t-test
Null hypothesis: mean = 10,0
Alternative: not equal
Computed t statistic = 0,639187
P-Value = 0,538627
Do not reject the null hypothesis for alpha = 0,05
…y tamaño muestral n para detectar media 9,8 con potencia >0.9:
Sample-Size Determination
Parameter to be estimated: normal mean
Desired power: 90,0% for mean = 10,0 versus mean = 10,2
Type of alternative: not equal
Alpha risk: 5,0%
Sigma: 0,173157 (to be estimated)
The required sample size is n=10 observations.
6
Práctica 4 vgaribay
2.2 a partir de estadísticos
2.2.a)
Hypothesis Tests
Sample standard deviation = 0,64
Sample size = 15
95,0% lower confidence bound for sigma: [0,49205]
Null Hypothesis: standard deviation = 0,5
Alternative: greater than
Computed chi-square statistic = 22,9376
P-Value = 0,0612927
Do not reject the null hypothesis for alpha = 0,05.
El apartado 2.1.a) se puede hacer también así, estimando previamente mu y sigma con
Describe/ Numeric Data / One-Variable Analysis
7
Práctica 4 vgaribay
2.2.b) Solución aproximada mediante Locate en el gráfico con la curva de potencia
Prob. aproximada de no detectar un incremento de  del 50% : 1-0,72 = 0,28
2.2.c) test de nivel 0.05  n / (0,75)>0.9
Sample-Size Determination
Parameter to be estimated: normal sigma
Desired power: 90,0% for sigma = 0,5 versus sigma = 0,75
Type of alternative: greater than
Alpha risk: 5,0%
The required sample size is n=27 observations.
8
Práctica 4 vgaribay
3 DOS Muestras INDEPENDIENTES Normales (Compare)
3.1 A partir de datos
3.1.1 Dos columnas de datos DatosContrastes.sgd TempTipo1 contra TempTipo2
3.1.1 a) Descripción comparada de las dos muestras.
Seleccionar variables y dejar todos los valores por defecto.
Nota:
En caso de que los datos se encuentren en una única columna con otra de códigos, los diagramas de
cajas se pueden dibujar con Plot/ExploratoryPlots/Box-and-WhiskerPlot/MultipleSamples
9
Práctica 4 vgaribay
3.1.1 b) Normalidad
Primero una variable, TempTipo1, y luego la otra, TempTipo2
10
Práctica 4 vgaribay
Ampliación: Tests de ajuste
Primero una muestra y luego la otra
Reducir nº de clases en el histograma
11
Práctica 4 vgaribay
3.1.1 c) Comparación medias 2 muestras independientes. Ampliamos el apartado 3.1.1.a)
incorporando el contrastes de comparación de medias (1 lado), previa comparación de varianzas.
Tests de Hipótesis > Pane Options para indicar , , un lado y sigmas iguales:
12
Práctica 4 vgaribay
Salidas de Statgraphics:
F-test to Compare Standard Deviations
Null hypothesis: sigma1 = sigma2
Alt. hypothesis: sigma1 NE sigma2
F = 0,956938 P-value = 0,708066
Do not reject the null hypothesis for alpha = 0,05.
t test to compare means
Null hypothesis: mean1 = mean2
Alt. hypothesis: mean1 < mean2
assuming equal variances: t = -1,60943 P-value = 0,0540328
Do not reject the null hypothesis for alpha = 0,05.
13
Práctica 4 vgaribay
3.1.2 Una columna de datos y otra de códigos que definen los dos grupos Datos robles.sgd
Marcar “Data (Potasio) and Code (Variedad) Columns”
Comparar medias y varianzas
F-test to Compare Standard Deviations
Null hypothesis: sigma1 = sigma2
Alt. hypothesis: sigma1 NE sigma2
F = 0,515507 P-value = 0,216385
Do not reject the null hypothesis for alpha = 0,05.
t test to compare means
Null hypothesis: mean1 = mean2
Alt. hypothesis: mean1 NE mean2
assuming equal variances: t = 2,34645 P-value = 0,024576
Reject the null hypothesis for alpha = 0,05.
14
Práctica 4 vgaribay
3.2 A partir de estadísticos
Comparación de medias,
3.2.a) comparación previa de igualdad de varianzas (s1=3,16227766017 ; s2= 4,472135955)
Los datos son compatibles con la igualdad de sigmas (a nivel 0.05; de hecho, p-valor = 0,236515)
15
Práctica 4 vgaribay
3.2.a) comp de medias (dos lados, =0.10, varianzas iguales )
Null Hypothesis: difference between means = 0,0
Alternative: not equal
Computed t statistic = 0,197009
P-Value = 0,845551
Do not reject the null hypothesis for alpha = 0,1.
(Equal variances assumed).
16
Práctica 4 vgaribay
4 DOS Muestras APAREADAS Normales (Compare)
A partir de datos (archivo DatosContrastes, dos columnas) H1: mu_sinpin-mu_pin > 0
Pane Options: H1:musinpin-mupin>0
Hypothesis Tests for Sin Pintar - Pintados
t-test
Null hypothesis: mean = 0
Alternative: greater than
Computed t statistic = 5,3936
P-Value = 0,00147879
Reject the null hypothesis for alpha = 0,05.
17
Práctica 4 vgaribay
5 CONTRASTES SOBRE PROPORCIONES
5.1 a y b Una muestra, a partir de estadísticos (Describe)
Hypothesis Tests
Sample proportion = 0,028125
Sample size = 8000
Approximate 95,0% lower confidence bound for p: [0,0251863]
Null Hypothesis: proportion = 0,025
Alternative: greater than
P-Value = 0,0396738
Reject the null hypothesis for alpha = 0,05.
The StatAdvisor
This analysis shows the results of performing a hypothesis test concerning the
proportion (theta) of a binomial distribution. The two hypotheses to be tested
are:
Null hypothesis:
theta = 0,025
Alternative hypothesis: theta > 0,025
In this sample of 8000 observations, the sample proportion equals 0,028125.
Since the P-value for the test is less than 0,05, the null hypothesis is rejected
at the 95,0% confidence level. The confidence bound shows that the values
of theta supported by the data are greater than or equal to 0,0251863.
(Locate) Potencia(3) = 0,86 aprox.
18
Práctica 4 vgaribay
5.1 c) Tamaño muestral para detectar p=0.03 con prob 0,99
Binomial p, Ho: p=0.025 H1: p>0.025
1 lado, n / (0.03)=0.99 Dif=0.03-0.025 =0.05
Sample-Size Determination
Parameter to be estimated: binomial parameter
Desired power: 99,0% for proportion = 0,025 versus proportion = 0,03
Type of alternative: greater than
Alpha risk: 5,0%
The required sample size is n=17114 observations.
The StatAdvisor
This procedure determines the sample size required when estimating the proportion of a binomial distribution. 17114 observations are
required to have a 99,0% chance of rejecting the hypothesis that theta=0,025 when the true theta=0,03 (using a one-sided test).
19
Práctica 4 vgaribay
5.2
Dos muestras, a partir de estadísticos (Compare)
Hypothesis Tests
Sample proportions = 0,042 and 0,064
Sample sizes = 500 and 500
Approximate 95,0% confidence interval for difference between proportions: [-0,0497375;0,00573753]
Null Hypothesis: difference between proportions = 0,0
Alternative: not equal
Computed z statistic = -1,55267
P-Value = 0,120501
Do not reject the null hypothesis for alpha = 0,05.
Warning: normal approximation may not be appropriate for small sample
sizes.
The StatAdvisor
This analysis shows the results of performing a hypothesis test concerning
the difference between the proportions (theta1-theta2) of two samples from
binomial distributions. The two hypotheses to be tested are:
Null hypothesis:
theta1-theta2 = 0,0
Alternative hypothesis: theta1-theta2 <> 0,0
In the first sample of 500 observations, the sample proportion equals 0,042. In the second sample of 500 observations, the sample
proportion equals 0,064. Since the P-value for the test is greater than or equal to 0,05, the null hypothesis cannot be rejected at the
95,0% confidence level. The confidence interval shows that the values of theta1-theta2 supported by the data fall between -0,0497375
and 0,00573753.
NOTE: this test uses a normal approximation. Because of the small sample sizes, this approximation may not be valid.
20