1.- Determine la magnitud de la fuerza F de tal manera que la fuerza
Anuncio
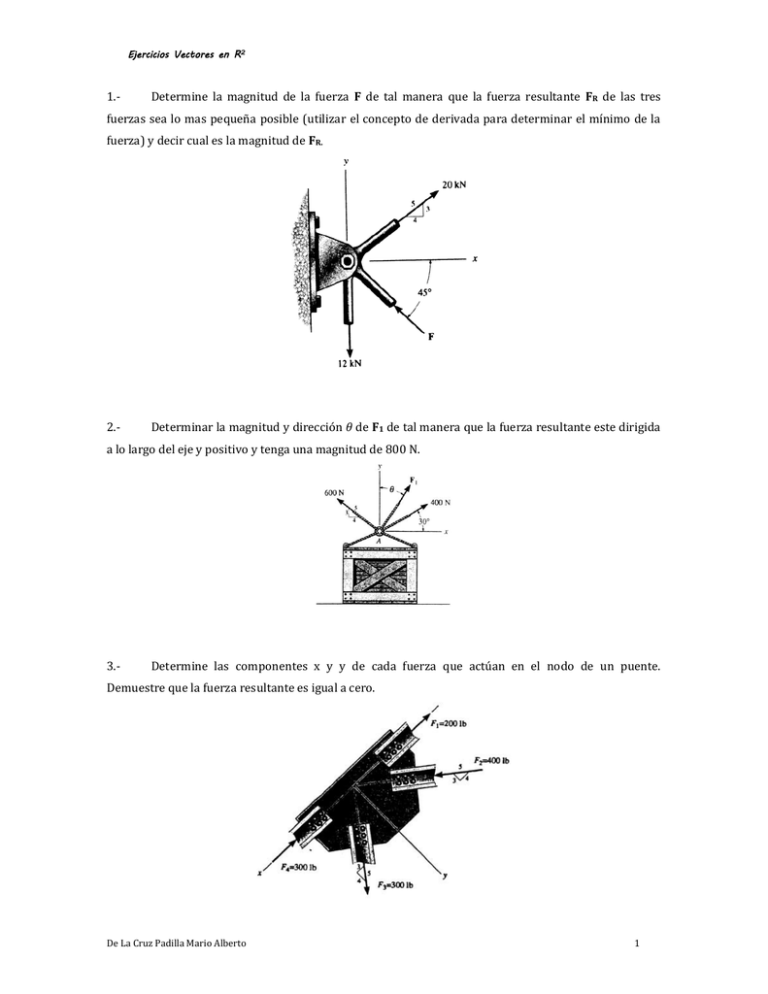
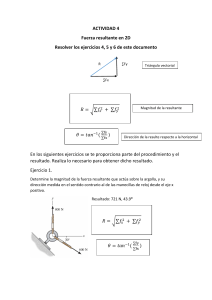
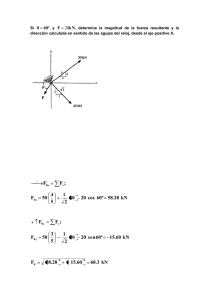
Ejercicios Vectores en R2 1.- Determine la magnitud de la fuerza F de tal manera que la fuerza resultante FR de las tres fuerzas sea lo mas pequeña posible (utilizar el concepto de derivada para determinar el mínimo de la fuerza) y decir cual es la magnitud de FR. 2.- Determinar la magnitud y dirección 𝜃 de F1 de tal manera que la fuerza resultante este dirigida a lo largo del eje y positivo y tenga una magnitud de 800 N. 3.- Determine las componentes x y y de cada fuerza que actúan en el nodo de un puente. Demuestre que la fuerza resultante es igual a cero. De La Cruz Padilla Mario Alberto 1 Ejercicios Vectores en R2 4.- Las tres fuerzas concurrente que actúan en el gancho producen una fuerza resultante 𝑭𝑹 = 0. Si 2 𝑭𝟐 = 𝑭𝟏 y F1 esta a 90º de la fuerza F2 como se muestra. Determine la magnitud de F3 requerida 3 expresada en términos de F1 y el ángulo 𝜃. 5.- Determine la magnitud de la fuerza F de tal manera que FR de las tres fuerzas es lo más pequeño posible. ¿Cuál es la mínima magnitud de FR? 6.- Las tres fuerzas concurrentes que actúan en el poste generan una fuerza resultante de cero. Si 1 𝑭𝟐 = 𝑭𝟏 y F1 debe estar a 90º de F2 como se muestra. Determine la magnitud de F3 requerida para 2 expresada en términos de F1 y 𝜃 De La Cruz Padilla Mario Alberto 2 Ejercicios Vectores en R2 1.- La fuerza que produce la menor fuerza resultante es de 11.3 kN y esta fuerza resultante es de √128𝑘𝑁. 2.- La magnitud de F1 es de 275 N a lo largo del eje y positivo. 3.- Las componentes de las fuerza son: 𝐹1𝑥 = −200 lb 𝐹1𝑦 = 0 lb 𝐹2𝑥 = 320 lb 𝐹2𝑦 = −240 lb 𝐹3𝑥 = 180 lb 𝐹3𝑦 = 240 lb 𝐹4𝑥 = −300 lb 𝐹1𝑦 = 0 lb 4.- Se tiene que 𝑭𝟑 = 1.2𝑭𝟏 con un ángulo de 𝜃 = 63.7° 5.- Se tiene que F=5.96 kN y la fuerza resultante mínima es FR= 2.33 kN 6.- La magnitud de 𝐹3 = 1.12 𝐹1 con 𝜃 = 116.57 De La Cruz Padilla Mario Alberto 3