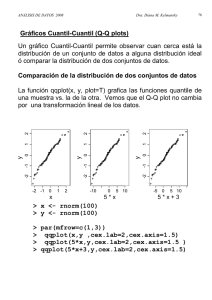
Q-Q Plots
Anuncio

Q-Q Plots El cuantil q de F(x) es el número xq tal que F(xq) = q. Si F-1 es la inversa de F, entonces xq = F-1(q) Un estimado razonable de la función de distribución F(x) de una variable aleatoria X es F’n(x) definida una proporción de las muestras que son más pequeñas que xi, es decir F’(xi) = i/n. No obstante, i/n, es igual a 1 cuando i = n, mientras que la mayoría de las distribuciones teóricas tienden a 1 cuando x va a infinito. De modo que se usa: F’’(xi) = F’(xi) – 0.5/n = (i – 0.5)/n Para n grande el ajuste es bastante pequeño. ?? Una forma fácil de ver si los datos (xi) se ajustan a una función de distribución teórica determinada es graficando los puntos (x1, 0.5/n), (x2,1.5/n), ...,(xn, (n-0.5)/n) y comparando este resultado con el gráfico de la función de distribución teórica que creemos que se ajusta a nuestros datos. El problema es que muchas funciones de distribución tienen forma de S y es muy difícil para el ojo humano ver qué tan parecidas son las S´s ?? La segunda forma es usando un qqplot. Sea qi=(i-0.5)/n para i=1,2,....,n, 0< qi < 1. Para cualquier conjunto de datos continuo un qqplot es un gráfico de los cuantiles de la función de distribución teórica xqiT que se obtienen como: xqiT = F-1(qi), versus los cuantiles de la distribución muestral F’’(x), llamados xqiM = F-1(qi), para i = 1, 2, ..., n. Si las funciones de distribución tienen una inversa, es muy fácil determinar los xqi. En otros casos, se tienen que usar tablas e interpolar los valores si es necesario. Por ejemplo, para una normal (0,1), se usa la siguiente aproximación: xqi = 4.9[qi 0.14 – (1 - qi) 0.14 ] Ejemplo: La diferencia entre los valores medidos y aquellos que predice un modelo son llamados errores. Los errores para 8 predicciones de un modelo fueron: -0.04, -0.19, 0.14, -0.09, -0.14, 0.19, 0.04 y 0.09. Compruebe que los errores se distribuyen normal (0,1). i xi S qi = (i - .5)/n 1 -0.19 .06 2 -0.14 0.19 3 -0.09 0.32 4 -0.04 0.44 5 0.04 0.56 6 0.09 0.69 7 0.14 0.81 8 0.19 0.94 Finalmente, usando una distribución teórica calculamos los cuantiles téoricos xqiT i xqi S xqi t qi = (i - .5)/n 1 -0.19 -1.54 .06 2 -0.14 -0.89 0.19 3 -0.09 -0.49 0.32 4 -0.04 -0.16 0.44 5 0.04 0.16 0.56 6 0.09 0.49 0.69 7 0.14 0.89 0.81 8 0.19 1.54 0.94 El qqplot queda como sigue: QQPlot Valores Medidos 0.3 0.2 0.1 0 -2 -1 -0.1 0 1 2 -0.2 -0.3 Valores Teóricos Notas: ?? La distribución teórica es una normal (0, 1). ?? Si la línea no tiene intersección con 0 en el eje y, y pendiente 1, las funciones de distribución son distintas. Si la línea tiene pendiente 1 (y no se intercepta con 0 en el eje y), la diferencia de las dos distribuciones es constante. ?? Aunque las dos funciones de distribución sean iguales, la línea puede no ser recta si se tienen pocas muestras.