Tipos de radiaciones electromagnéticas según λ.
Anuncio
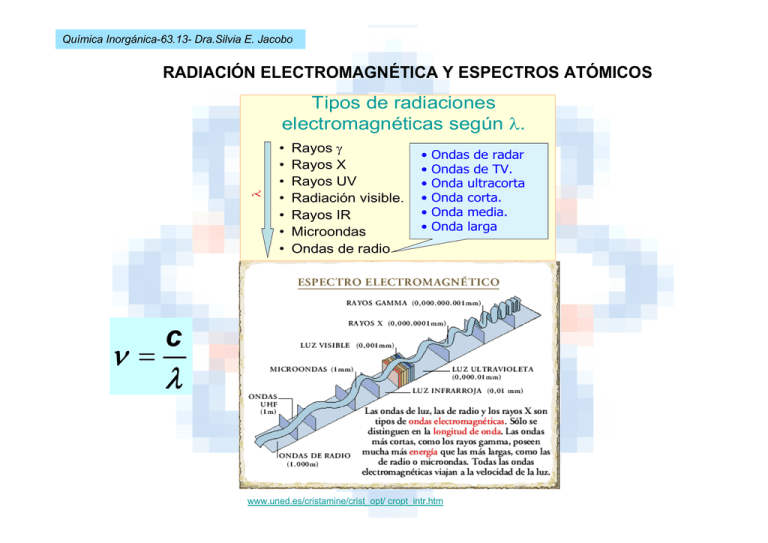
Química Inorgánica-63.13- Dra.Silvia E. Jacobo RADIACIÓN ELECTROMAGNÉTICA Y ESPECTROS ATÓMICOS λ Tipos de radiaciones electromagnéticas según λ. ν = • • • • • • • Rayos γ Rayos X Rayos UV Radiación visible. Rayos IR Microondas Ondas de radio • • • • • • Ondas de radar Ondas de TV. Onda ultracorta Onda corta. Onda media. Onda larga c λ www.uned.es/cristamine/crist_opt/ cropt_intr.htm Química Inorgánica-63.13- Dra.Silvia E. Jacobo ESPECTRO ELECTROMAGNETICO www.puc.cl/sw_educ/qda1106/ CAP2/2B/2B1/ Química Inorgánica-63.13- Dra.Silvia E. Jacobo Hipótesis de Plank. Cuantización de la energía El estudio de estas rayas espectrales permitió relacionar la emisión de radiaciones de determinada “l“ con cambios energéticos asociados a saltos electrónicos. Así Plank supuso que la energía estaba cuantizada, al igual que ocurría con la masa o la carga; es decir, la energía absorbida o desprendida de los átomos sería un múltiplo de una cantidad establecida o “cuanto” que correspondería a la energía correspondiente a la energía emitida o absorbida por un átomo. Así, si un átomo emite radiación de frecuencia “ν”, la energía desprendida por dicho átomo sería: E = h ×ν Y la energía total emitida será por tanto un múltiplo de esta cantidad, según el número de átomos que emitan: E = n h x n, en donde h = 6,626 10–34 J x s (Constante de Plank) y "n" es un número entero (nº de átomos emisores), lo cual significa que la energía ganada o cedida por un átomo es un múltiplo de la cantidad de energía mínima (h x n). Química Inorgánica-63.13- Dra.Silvia E. Jacobo E = h ×ν ν = E mfotón = ------c2 hc/λ = ------c2 h = -------λc que nos dice que la masa del fotón depende de la longitud de onda de la radiación luminosa. c λ Química Inorgánica-63.13- Dra.Silvia E. Jacobo Ejemplo: Calcula la energía de fotones de rayos X cuya longitud de onda es de 0,6 nm. (h = 6,625 x 10–34 J s) 3 × 108 m s −1 17 s = 5 × 10 ν= = λ 0,6 × 10−9 m c E = h x ν = 6,625 x 10–34 J s x 5 x 1017 s–1 E = 33,125 x 10–17 J = 3,3125 x 10–16 J Química Inorgánica-63.13- Dra.Silvia E. Jacobo Química Inorgánica-63.13- Dra.Silvia E. Jacobo Espectros atómicos. Cuando a los elementos en estado gaseoso se les suministra energía (descarga eléctrica, calentamiento...) éstos emiten radiaciones de determinadas longitudes de onda. Estas radiaciones dispersadas en un prisma de un espectroscopio se ven como una serie de rayas, y el conjunto de las mismas es lo que se conoce como espectro de emisión. Igualmente, si una luz continua atraviesa una sustancia, ésta absorbe unas determinadas radiaciones que aparecen como rayas negras en el fondo continuo (espectro de absorción). Series espectrales. Las diferentes líneas que aparecieron en el espectro del hidrógeno se podían agrupan en diferentes series cuya longitud de onda es más parecida: Serie Lyman: zona ultravioleta del espectro. Serie Balmer: zona visible del espectro. Serie Paschen zona infrarroja del espectro. Serie Bracket: zona infrarroja del espectro. Serie Pfund: zona infrarroja del espectro Química Inorgánica-63.13- Dra.Silvia E. Jacobo Series espectrales n=∞ n=6 n=5 n=4 Pfund Bracket n=3 n=2 Paschen Balmer ΔE = h · ν n=1 Lyman SERIES: Lyman Balmer Paschen Bracket Pfund Espectro UV Visible Infrarrojo Química Inorgánica-63.13- Dra.Silvia E. Jacobo Niveles permitidos Energía (para el átomo de hidrógeno) n=∞ n=5 n=4 E= 0J E = –0,87 · 10–19 J E = –1,36 · 10–19 J n=3 E = –2,42 · 10–19 J n=2 E = –5,43 · 10–19 J n=1 E = –21,76 · 10–19 J ⎛ 1 1 ⎞ = R ×⎜ 2 − 2 ⎟ λ ⎝ n1 n2 ⎠ 1 Química Inorgánica-63.13- Dra.Silvia E. Jacobo EFECTO FOTOELECTRICO Ecinética 1 = m v 2 = h × ν − E ioniz = h (ν − ν 0 ) 2 Ayuntamiento La Coruña (ver animación) Química Inorgánica-63.13- Dra.Silvia E. Jacobo Ejercicio A: Determina la energía cinética con la que será expulsado un electrón del cesio al emplear una radiación de 850 nm si sabemos que la energía umbral del Cs es 6,22 x 10–19 J. Ecinética 1 = m v 2 = h × ν − E ioniz = h (ν − ν 0 ) 2 Química Inorgánica-63.13- Dra.Silvia E. Jacobo ENERGÍA DE VIBRACIÓN E = h ×ν Química Inorgánica-63.13- Dra.Silvia E. Jacobo ESPECTROSCOPIA INFRARROJA Química Inorgánica-63.13- Dra.Silvia E. Jacobo Química Inorgánica-63.13- Dra.Silvia E. Jacobo RELACION DE DE BROGLIE h: Constante de Planck, cuyo valor es 6,626 x 10 –34 Js p=h/λ Esta relación muestra que cuanto mayor sea el momento lineal de la partícula, menor será la longitud de onda de su función de onda. h λ= m ×v λ: longitud de onda Química Inorgánica-63.13- Dra.Silvia E. Jacobo Principio de incertidumbre de Heisenberg Es imposible especificar, simultáneamente y con exactitud, la posición y el momento lineal de una partícula. Esta conclusión se expresa cuantitativamente de la siguiente manera: Siendo Δx la incertidumbre de la posición de la partícula y la incertidumbre de su momento lineal Δp, entonces: Δx · Δp ≥ h 4π Química Inorgánica-63.13- Dra.Silvia E. Jacobo ECUACION DE ONDA DE SCHRÖDINGER Química Inorgánica-63.13- Dra.Silvia E. Jacobo ECUACION DE ONDA DE SCHRÖDINGER m: masa de la partícula V: energía potencial h = h / 2π Química Inorgánica-63.13- Dra.Silvia E. Jacobo Las soluciones, o funciones de onda, son funciones matemáticas que dependen de unas variables que sólo pueden tomar valores enteros. Estas variables de las funciones de onda se denominan números cuánticos: número cuántico principal, (n), angular (l) y número cuántico magnético (ml). Estos números describen el tamaño, la forma y la orientación en el espacio de los orbitales en un átomo. • El número cuántico principal (n) describe el tamaño del orbital, por ejemplo: los orbitales para los cuales n=2 son más grandes que aquellos para los cuales n=1. Puede tomar cualquier valor entero empezando desde 1: n=1, 2, 3, 4, etc. • El número cuántico del momento angular orbital (l) describe la forma del orbital atómico. Puede tomar valores naturales desde 0 hasta n-1 (siendo n el valor del número cuántico principal). Por ejemplo si n=5, los valores de l pueden ser: l= 0, 1 ,2, 3, 4. • El número cuántico magnético (ml), determina la orientación espacial del orbital. Se denomina magnético porque esta orientación espacial se acostumbra a definir en relación a un campo magnético externo. Puede tomar valores enteros desde -l hasta +l. Por ejemplo, si l=2, los valores posibles para m son: ml=-2, -1, 0, 1, 2. • El número cuántico de espín (s), sólo puede tomar dos valores: +1/2 y -1/2 Química Inorgánica-63.13- Dra.Silvia E. Jacobo NÚMEROS CUANTICOS Química Inorgánica-63.13- Dra.Silvia E. Jacobo NIVELES DE ENERGIA Química Inorgánica-63.13- Dra.Silvia E. Jacobo EXPRESIÓN DE LA FUNCION DE ONDA Rnl(r) = f(r)(Z/a0)3/2 e-r/2 Química Inorgánica-63.13- Dra.Silvia E. Jacobo ORBITALES ATOMICOS Orbital s Química Inorgánica-63.13- Dra.Silvia E. Jacobo Química Inorgánica-63.13- Dra.Silvia E. Jacobo ORBITALES P Química Inorgánica-63.13- Dra.Silvia E. Jacobo Química Inorgánica-63.13- Dra.Silvia E. Jacobo ORBITALES D Química Inorgánica-63.13- Dra.Silvia E. Jacobo ORBITALES F Química Inorgánica-63.13- Dra.Silvia E. Jacobo APANTALLAMIENTO La carga nuclear efectiva, (Zeff) es igual al número de protones en el núcleo(Z ó número atómico) menos el promedio de electrones entre el electrón en cuestión y el núcleo (S) : Química Inorgánica-63.13- Dra.Silvia E. Jacobo Subniveles en la tabla periódica Química Inorgánica-63.13- Dra.Silvia E. Jacobo

