Tabla de relaciones entre los dominios temporal y frecuencial
Anuncio

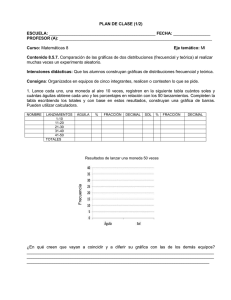
7.19. Tablas útiles 7.19. 157 Tablas útiles Muestreo dominio frecuencial ( f ) dominio temporal dominio frecuencial (Ω) Xc ( f ) xc (t) Xc ( Ω ) PT ( f ) = 1 T ∑ δ( f 1 T PT ( f ) ∑ k Xc ( f = ∑ k = 1 T 2π F (ω ∑Xc 2π k Xs ( Ω ) = p T (t) = ∑ xc (nT )δ(t nT ) = n Fs Xc (ω 2π h xs (t) = xc (t) kFs ) X (e jω ) = Xs ( f )j f =ω Fs = 1 T PT (Ω) = nT ) n k Xs ( f ) = Xc ( f ) = p T (t) = ∑ δ(t kFs ) s 2π T ∑ δ(Ω 1 2π Xc ( Ω ) 1 T kΩs ) n ∑ k Xc ( Ω PT (Ω) kΩs ) ω 2πT Xs (Ω)jΩ=ω Ωs = ω kFs ) 1 T x [n] = xc (t)jt=nT = ∑ Ωs Xc (ω 2π T 2π kΩs ) k i 2πk ) = 1 T ∑Xc T1 (ω 2πk ) k Reconstrucción dominio frecuencial ( f ) dominio temporal dominio frecuencial (Ω) Y (e jω ) y[n] Y (e jω ) ys (t) = ∑ y[n]δ(t nT ) Ys ( f ) = Y (e jω )jω = f 2π = f 2πT Fs Hr ( f ) = ( T, j f j < F2s hr ( t ) = 0, j f j > F2s ω = f 2π Fs = f 2πT si j f j < Ωs sen πt T πt T = sinc t T yr (t) = ∑n y[n]hr (t nT ) Yr ( f ) = Hr ( f )Ys ( f ) = TY (e jω ) Ys (Ω) = Y (e jω )jω =Ω 2π =ΩT n Fs 2 Procesamiento Digital de Señales = ∑n y[n] sinc t nT T Hr (Ω) = ( T, jΩj < Ω2s = πT 0, jΩj > Ω2s = πT Yr (Ω) = Hr (Ω)Ys (Ω) = TY (e jω )jω =Ω 2π =ΩT Ωs si Ωj < Ωs 2 = πT U.N.S. 2011 7. Muestreo de señales 158 Procesamiento discreto de señales continuas dominio frecuencial ( f ) dominio temporal dominio frecuencial (Ω) Xc ( f ) xc (t) Xc ( Ω ) X (e jω ) = 1 T h i Fs X ( ω 2πk ) c ∑ 2π X (e jω ) = x [n] = xc (t)jt=nT k 1 T ∑Xc T1 (ω 2πk ) k Y (e jω ) = H (e jω ) X (e jω ) Y (e jω ) = H (e jω ) X (e jω ) y[n] = h[n] x [n] Ys ( f ) = Y (e jω )jω = f 2π = f 2πT ys (t) = ∑y[n]δ(t nT ) Ys (Ω) = Y (e jω )jω =Ω 2π =ΩT Yr ( f ) = Hr ( f )Ys ( f ) yr (t) = ∑n y[n]hr (t nT ) Yr (Ω) = Hr (Ω)Ys (Ω) Fs Ωs n = ∑n y[n] sinc = TH (e jω) X (e jω)jω = f 2π Fs t nT T = TH (e jω) X (e jω)jω =Ω 2π Ωs =ΩT = f 2πT 8 jω H (e )jω = f 2π > > Fs > > = f 2πT > < si j f j < F2s Hc ( f ) = > > > 0, > > : si j f j > F2s 8 jω H (e )jω =Ω 2π > > Ωs > > =ΩT > < si jΩj < Ω2s Hc (Ω) = > >0, > > > : si jΩj > Ω2s Procesamiento continuo de señales discretas dominio frecuencial ( f ) Xc ( f ) = TX (e jω)jω = f 2π Fs dominio temporal xc (t) = ∑n x [n]hr (t nT ) Xc (Ω) = TX (e jω)jω =ΩT Yc ( f ) = Hc ( f ) Xc ( f ) y c ( t ) = hr ( t ) x c ( t ) Y (e jω ) = T1 Yc ( f )j f =ω Fs y[n] = yc (t)jt=nT 2π H (e jω ) = Hc ( f )j f =ω Fs , jω j < π 2π Procesamiento Digital de Señales dominio frecuencial (Ω) Yc (Ω) = Hc (Ω) Xc (Ω) Y (e jω ) = T1 Yc (Ω)jΩ=ω Ωs = ω 2π T H (e jω ) = Hc (Ω)jΩ= ωT , jω j < π U.N.S. 2011 7.19. Tablas útiles 159 Decimación x f [n] = x [n] h PB [n] = ∑ x [`]h PB [n , X f e jω = HPB e jω X e jω `] ` , Xd e jω = xd [n] = x f [nM ] 1 M M 1 j ∑ Xf e ( ω 2πr M ) r =0 Interpolación xe [n] = ( x [n/L], si n = 0, 0, en caso contrario. xi [ n ] = x e [ n ] h I [ n ] = = ∑ x [`]h[n L, ∑ xi [`]h[n 2L, . . . , `] ` ` L] , Xe e jω = X e jωL Xi e jω = H I e jω Xe e jω ` = L X e jωL , jω j < π/L Cambio de la frecuencia de muestreo por un factor no entero Intercambio de filtrado y sub/sobre muestreo Procesamiento Digital de Señales U.N.S. 2011 160 Procesamiento Digital de Señales 7. Muestreo de señales U.N.S. 2011