Ejemplo de informe de práctica

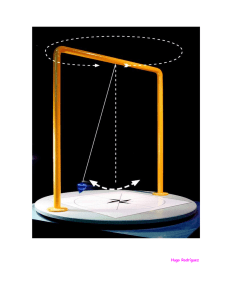
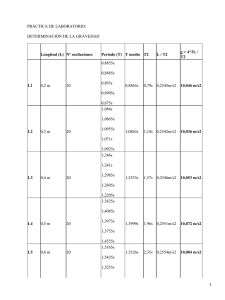
Ejemplo de informe:
Péndulo simple
Introducción
Se trata de medir la aceleración de la gravedad mediante un péndulo simple. Para
oscilaciones pequeñas, el periodo T viene dado [véase cualquier libro de Física
General] por la longitud del péndulo l y la aceleración de la gravedad g:
l
T = 2π
g
(Ecuación 1)
Así pues, midiendo T y l podremos determinar g:
l
g = 4π 2
T
2
(Ec. 2)
Además, lo haremos para varias longitudes l para comprobar que efectivamente se
cumple la ley usada.
Metodología
• Como el error relativo, tanto de la longitud l como del periodo T, disminuye
al aumentar l, dejamos que el péndulo sobresalga por el borde de la mesa, para
que pueda llegar hasta el suelo.
• Como el corcho de las pletinas, que aprietan y soportan el hilo, está
desgastado, el punto exacto de suspensión tiene más error. Por ello hemos
insertado unas placas rígidas de plástico, con un borde bien afilado, y hemos
medido la longitud del hilo hasta ese borde.
• Como es menos preciso medir la longitud desde el centro de la bola (donde
está su centro de masas), lo hacemos desde su parte superior (con una cinta
métrica) y le sumamos la mitad de su diámetro d, medido con un calibre.
Como la precisión del calibre es mucho mayor, despreciamos el error en d.
• Para eliminar un posible error sistemático en la calibración de la cinta
métrica, medimos una longitud (la mayor) con tres cintas distintas. Como
obtenemos el mismo resultado, en mm, consideramos como error estimado
∆l = 1 mm (la sensibilidad de la cinta).
• La sensibilidad del cronómetro es de 0.01s, pero la desviación típica de las
medidas es bastante mayor, por lo que tomamos ésta como error de tiempo.
Medidas
• Diámetro de la bola: d = 20.1 ± 0.1 mm
• Medimos la longitud del hilo, desde la parte superior de la bola, y le sumamos el
radio de ésta (10 mm).
• Para cada una de cuatro longitudes l, medimos la duración t de 10 oscilaciones y
repetimos la medida 5 veces. Tenemos siempre cuidado de que las oscilaciones
sean pequeñas (de unos 5 cm de amplitud).
Datos medidos (“crudos”)
Datos derivados
T (s)
∆T (s)
9.45 0.02
0.945
0.002
409+10 13.15, 13.04, 12.95, 13.01, 13.09
13.05 0.03
1.305
0.003
773+10 17.66, 17.65, 17.72, 17.66, 17.70
17.68 0.01
1.768
0.001
944+10 19.50, 19.63, 19.63, 19.64, 19.54
19.59 0.03
1.959
0.003
l(mm)
Duración t de 10 oscilaciones (s)
207+10
9.47, 9.41, 9.48, 9.40, 9.49
t
∆t
Resultados
Como primer tratamiento más sencillo, utilizamos la ecuación 2 para obtener
el valor de g para cada longitud l. Para l = 954 mm:
2 0.954m
2
g = 4π
=
9
.
814
m/s
(1.959s) 2
∆g ∆l
∆T
0.003s
1mm
=
+2
=
+2
= 0.001 + 0.003
g
l
T
1.959s
954mm
Donde podemos ver que para mejorar la precisión de g deberíamos sobre todo
disminuir el error de T. Ahora
∆g = 0.004 × 9.814m/s 2 = 0.04m/s 2
Repitiendo lo mismo para todos los valores de l obtenemos
l (m)
0.217
g (m/s2)
9.59 ± 0.07
0.419
0.783
0.954
9.71 ± 0.05
9.89 ± 0.07
9.81 ± 0.04
Si sacamos la media de los valores y su desviación típica:
g = 9.75 ± 0.06 m/s2
(valor medido, método 1)
Resultados (cont.)
Alternativamente, ajustamos los datos de l frente a t con una recta que pase por
el origen. Su pendiente, multiplicada por 4π2, debe ser g. La gráfica está en la
página siguiente. Del ajuste (realizado mediante un paquete estadístico
estándar) obtenemos una pendiente de p = 0.249 ± 0.002 m/s2 y un valor de
g = 4π2 p = 9.83 ± 0.07 m/s2
(valor medido, método 2)
El valor esperado para Madrid lo obtenemos del Handbook of Chemistry and
Physics (ver apéndice):
Latitud = 40o 26’ N, Altura = 700 m =>
g = 980.171 + (980.261 - 980.171)*26/60 + 0.2160 cm/s2 =
= 9.804 m/s2
(valor esperado)
Gráfica de l frente a T2
1.0
0.8
0.6
l (m)
0.4
l = 0.249 m/s2 × T2
0.2
0.0
0
1
2
T2 (s2)
3
4
Discusión y comentarios
• El valor medido tiene un error de sólo un 0.3-0.5% con respecto al esperado,
dependiendo del método usado para procesar los datos. Esta discrepancia está
dentro del error experimental estimado del ~0.7%. Además, hemos verificado
la ecuación 2, que se cumple con gran precisión.
• Una posible fuente de error es que la masa del hilo eleve la posición del
centro de masas del conjunto bola-hilo y disminuya la longitud efectiva l. Para
hacer un tratamiento riguroso de este efecto debemos considerar la teoría del
“péndulo físico” [ver, por ejemplo P.A.Tipler, Física General]. Pero podemos
hacer una estimación sencilla de la magnitud del efecto:
Masa medida de la bola: mb = 125.5 g
Masa medida del hilo: mh = 0.2 g
=> ∆l/l = ((mh l/2)/(mb+ mh)) / l ≅ mh / 2mb = 8 × 10-4
Que es comparable al error de medida de ≈ 1mm / 1m = 10-3
• De todas formas, hemos visto que la mayor fuente del error ∆g proviene de la
medida del periodo, que podríamos haber mejorado midiendo más oscilaciones.
Sugerencias
• Para aumentar aún más la longitud del péndulo, y disminuir así el error
relativo de la medida, convendría disponer de una barra de soporte más larga, o
de una forma de colgarlo del techo.
• Para disminuir el error debido a la masa del hilo, y también para disminuir el
efecto del rozamiento (aumentando la fuerza de la gravedad con respecto a
éste), convendría aumentar la masa de la bola.
Apéndice: tabla de g en la Tierra
Fuente: Handbook of Chemistry and Physics, edición 71 (1990-91). Pag. 14-7