EL PLANO CARTESIANO El plano cartesiano está formado por dos
Anuncio

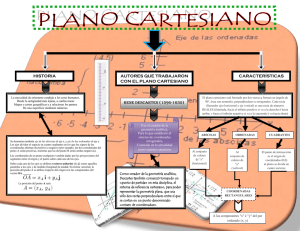
_______________________________________________________________________________ SEGUNDO BIMESTRE SEMANA 16-17 MATEMATICA II 2do. Básico EL PLANO CARTESIANO El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen. El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se representa como: P (x, y) Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento: 1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero. 2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas. Elaborado por Cynthia Rodas _______________________________________________________________________________ Ejemplos: Localizar el punto A (-4, 5) en el plano cartesiano. Este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano. Determinar las coordenadas del punto M. Las coordenadas del punto M son (3,-5). De lo anterior se concluye que: Para determinar las coordenadas de un punto o localizarlo en el plano cartesiano, se encuentran unidades correspondientes en el eje de las x hacia la derecha o hacia la izquierda y luego las unidades del eje de las y hacia arriba o hacia abajo, según sean positivas o negativas, respectivamente. Elaborado por Cynthia Rodas _______________________________________________________________________________ Doña Lupe nos ha dicho que su farmacia está dentro del centro de la ciudad. Supongamos que deseamos saber la ubicación exacta de la farmacia de Doña Lupe Una vez que ya estamos en el centro le preguntamos a un policía para que nos oriente. El policía nos ha dicho que caminemos 5 cuadras hacía el este y 6 cuadras hacía el norte para llegar a la farmacia. La cantidad de cuadras que tenemos que caminar las podemos entender como coordenadas en un plano cartesiano. Lo anterior lo podemos expresar en un plano cartesiano de la siguiente manera: Para el problema planteado, el origen del plano será el punto de partida que es en donde le preguntamos al policía sobre la ubicación de la farmacia. FUNCIONES En matemáticas, una función, aplicación o mapeo f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por: Comúnmente, el término función se utiliza cuando el codominio son valores numéricos, reales o complejos. Entonces se habla de función real o función compleja mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones. Elaborado por Cynthia Rodas _______________________________________________________________________________ FUNCION LINEAL La función lineal es la más simple dentro de las formas que puede adoptar una relación entre variables económicas, pero desempeñan un importante papel en la formulación de los problemas económicos. Una función lineal tiene la forma general Donde a y b son números reales, el coeficiente a es la pendiente de la recta que representa a la función y siempre es distinta de cero, el término independiente b es la ordenada al origen, que gráficamente representa la intersección de la recta con el eje de las ordenadas en el punto de coordenadas (0,b). La variable independiente es x, a la cual le asignamos valores para obtener y. Estas funciones se caracterizan porque un cambio unitario en la variable independiente (x), provoca un cambio proporcional en la variable dependiente (y). La tasa de cambio está representada por la constante a Elaborado por Cynthia Rodas _______________________________________________________________________________ FUNCION CUADRATICA Una función cuadrática es toda función que pueda escribirse de la forma f(x) = a x2 + b x + c, donde a, b y c son números cualesquiera, con la condición de que a sea distinto de 0. Ejemplo: 1. La función cuadrática más sencilla es f(x) = x2 cuya gráfica es: x f(x) = x2 -3 -2 -1 -0'5 0 0'5 1 2 3 9 4 1 0'25 0 0'25 1 4 9 Elaborado por Cynthia Rodas _______________________________________________________________________________ Funciones logarítmicas Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1, puesto que el resultado sería 0. Entonces se dan dos casos: Base mayor que la unidad (a > 1) Elaborado por Cynthia Rodas _______________________________________________________________________________ Funciones exponenciales Se llaman así a todas aquellas funciones de la forma f(x) = bx, en donde la base b, es una constante y el exponente la variable independiente. Estas funciones tienen gran aplicación en campos muy diversos como la biología, administración, economía, química, física e ingeniería. La definición de función exponencial exige que la base sea siempre positiva y diferente de uno (b>0 y b≠1). La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)=(-9)1/2 no tendrían sentido en los números reales. El dominio de la función exponencial está formada por el conjunto de los números reales y su recorrido está representado por el conjunto de los números. positivos. Elaborado por Cynthia Rodas