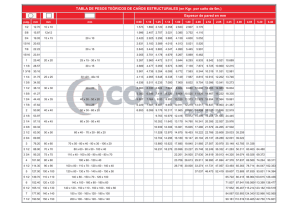
Solución del Ejercicio 4 Hallar aproximadamente ∫ 2 x(t)dt siendo x
Anuncio

Solución del Ejercicio 4 Hallar aproximadamente Z 2 x(t) dt 0 siendo x(t) la solución del problema de condiciones iniciales ( x 00 + t 2 x 0 − x = sen t, x(0) = 1, x 0 (0) = 1. Cambio de variables: x1 = x, x2 = x 0 . 0 x1 = x2 , x20 = x1 − t 2 x2 + sen t, x1 (0) = 1, x2 (0) = 1. 1/3 t 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 (x1 , x2 ) (1.0000, 1.0000) (1.2000, 1.2000) (1.4400, 1.4701) (1.7340, 1.7890) (2.0918, 2.1199) (2.5158, 2.4104) (2.9979, 2.5998) (3.5178, 2.6370) (4.0452, 2.5040) (4.5460, 2.2309) (4.9922, 1.8893) (x2 , x1 − t 2 x2 + sen t) (1.0000, 1.0000) (1.2000, 1.3507) (1.4701, 1.5942) (1.7890, 1.6546) (2.1199, 1.4524) (2.4104, 0.9469) (2.5998, 0.1863) (2.6370, -0.6653) (2.5040, -1.3653) (2.2309, -1.7082) h(x2 , x1 − t 2 x2 + sen t) (0.2000, 0.2000) (0.2400, 0.2701) (0.2940, 0.3188) (0.3578, 0.3309) (0.4240, 0.2905) (0.4821, 0.1894) (0.5200, 0.0373) (0.5274, -0.1331) (0.5008, -0.2731) (0.4462, -0.3416) 2/3 Todas las componentes de x1 menos la última suman 1.0000 1.2000 1.4400 1.7340 2.0918 2.5158 2.9979 3.5178 4.0452 4.5460 25.0885 Z 2 x(t) dt ' 25.0885 × 0.2 = 5.0177 =⇒ 0 3/3