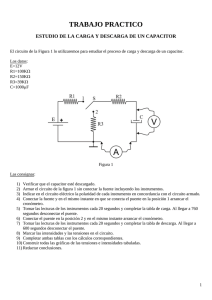
Carga y descarga de capacitores

Carga y descarga de capacitores
Autores
Frigerio, Paz
mapaz@vlb.com.ar
La Bruna,Gimena
labrugi@yahoo.com
Larreguy, María
merigl@yahoo.com
Romani, Julieta
julietaromani@hotmail.com
Laboratorio de Física 2 – Universidad Favaloro-Buenos Aires Octubre 2001
Resumen
Este experimento tiene como fin el estudio de la carga y la descarga de un
capacitor. A partir de un circuito RC estudiamos la variación de la tensión en el
capacitor cuando éste se carga y se descarga. De los datos experimentales
obtuvimos la constante de tiempo característica del circuito.
Introducción
En un circuito RC, conectado a una batería, a medida que pasa el tiempo, se observa un
aumento en la tensión del capacitor, mientras que la tensión en la resistencia disminuye. Esto es así
porque el capacitor se va cargando y, una vez que llega a su carga máxima, el circuito queda abierto
(ver figura 1). Sabemos, según las leyes de Kirchhoff que:
(1)
Vo = v R (t) + v(t)
donde Vo es el voltaje de la batería, vR(t) es la tensión en la resistencia y v(t) es la tensión en el
capacitor. A partir de la ecuación (1), la ecuación diferencial que describe el circuito es:
d
1
V
q (t) +
q (t) − = 0
(2)
dt
RC
R
Si el capacitor se encuentra inicialmente descargado, la condición inicial es q(0) = 0.
De la ecuación diferencial se obtiene la carga q en función del tiempo y, a partir de ella,
podemos obtener la corriente y las tensiones en función del tiempo. La tensión en el capacitor
durante su carga es:
v(t) = Vo 1 − e − t / τ
(3)
donde τ es la constante de tiempo característica:
(4)
τ = RC
En un circuito RC con un capacitor cargado, se produce la descarga del mismo a través
de la resistencia. La tensión en el capacitor va disminuyendo en el tiempo hasta hacerse cero, al
igual que la tensión en la resistencia. Según las leyes de Kirchhoff:
(5)
v R (t) = v(t)
La ecuación diferencial correspondiente al circuito es:
d
1
q (t) −
q (t) = 0
(6)
dt
RC
Conociendo la carga final qo a la que llegó el capacitor durante la carga, se obtiene la
condición inicial necesaria para la resolución de la ecuación (6).
La tensión en el capacitor durante su descarga es:
q
v(t) = o e − t / τ
(7)
C
(
)
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
1
Experimento
Para la realización de este experimento, utilizamos el circuito que se ilustra en la figura
1, tanto para la carga como la descarga del capacitor, simplemente moviendo los switch s1 y s2 para
cerrar uno u otro circuito RC.
Figura 1. Circuito utilizado para estudiar la carga y descarga de
un capacitor.
La fuente Vo es una batería de 9V. En ambos casos, medimos la tensión en el capacitor
con un sistema de adquisición de datos conectado a una PC. Realizamos el experimento dos veces
variando las resistencias R1 y R2.
Resultados
En primer lugar, analizamos la carga del capacitor para dos valores distintos de
resistencia R1 usando el mismo capacitor C. Graficamos la tensión obtenida en función del tiempo
de los datos experimentales, superpuesto por la curva teórica en base a la ecuación (3) como se
muestra en las figuras 2 y 3.
Tensión en el capacitor
9
8
7
v [Volt]
6
5
4
3
2
v teórico
1
0
0
10
20
30
40
50
60
70
80
t [seg]
Figura 2. Gráfico de la tensión en el capacitor en función del tiempo durante la carga del primer
experimento.
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
2
Tensión en el capacitor
9
8
7
v [Volt]
6
5
4
3
2
v teórico
1
0
0
20
40
60
80
100
120
t [seg]
Figura 3. Gráfico de la tensión en el capacitor en función del tiempo durante la carga del segundo
experimento.
Derivando la tensión en el capacitor se puede obtener una relación que permite obtener
la constante de tiempo característica τ del circuito:
d
v(t) = Vo − τ v(t)
(8)
dt
9
8
y = -18,757x + 8,4318
2
7
R = 0,9982
v [Volt]
6
5
4
3
2
1
0
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
dv/dt [Volt/seg]
Figura 4. Gráfico de la derivada de la tensión en el capacitor en función de la tensión
durante la carga del primer experimento.
En el primer caso obtuvimos una constante de tiempo de 18,76 s ± 0,02 s como puede
verse en la figura 4. En el segundo experimento, ilustrado en la figura 5, obtuvimos un valor para la
constante de tiempo de 10,86 s ± 0,02 s. El primer experimento fue realizado con una resistencia R1
menor que en el segundo experimento.
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
3
9
8
7
v [Volt]
6
5
4
3
y = -10,863x + 8,2273
2
2
R = 0,9973
1
0
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
dv/dt [Volt/seg]
Figura 5. Gráfico de la derivada de la tensión en el capacitor en función de la
tensión durante la carga del segundo experimento.
Repetimos la experiencia para la descarga del capacitor, también variando la resistencia
R2 con la que se descargaba el capacitor. Graficamos la tensión en función del tiempo en las figuras
6 y 7.
Tensión en el capacitor
9
8
v teórico
7
v [Volt]
6
5
4
3
2
1
0
0
20
40
60
80
100
120
140
t [seg]
Figura 6. Gráfico de la tensión en el capacitor en función del tiempo durante la
descarga del primer experimento con τ = 21,2 s.
Tensión en el capacitor
9
8
v teórico
7
v [Volt]
6
5
4
3
2
1
0
0
20
40
60
80
100
120
140
t [seg]
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
4
Figura 7. Gráfico de la tensión en el capacitor en función del tiempo durante la
descarga del segundo experimento con τ = 21,9 s.
Nuevamente buscamos una relación entre la derivada de la tensión y la tensión del
capacitor para poder obtener el valor de la constante de tiempo. Realizamos los gráficos 8 y 9 de los
cuales obtuvimos un valor de 21,19 s ± 0,02 s para el primer experimento y 21,89 s con un error
absoluto de 0,02 s para el segundo.
9
8
y = -21,194x + 0,0485
v [Volt]
7
2
R = 0,9993
6
5
4
3
2
1
0
-0,5
-0,4
-0,3
-0,2
-0,1
0,0
dv/dt [Volt/seg]
Figura 8. Gráfico de la derivada de la tensión en el capacitor en función de la tensión
durante la descarga del primer experimento.
9
8
y = -21,888x + 0,0971
7
2
R = 0,9989
v [Volt]
6
5
4
3
2
1
0
-0,5
-0,4
-0,3
-0,2
-0,1
0,0
dv/dt [Volt/seg]
Figura 9. Gráfico de la derivada de la tensión en el capacitor en función de la tensión
durante la descarga del segundo experimento.
Por último, graficamos los valores de τ obtenidos experimentalmente en función del
producto de las resistencias R y el capacitor C utilizados. El resultado obtenido se muestra en la
figura 10.
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
5
Constante de tiempo
característica experimental [s]
24
22
y = 0,9968x
20
R = 0,9986
2
18
16
14
12
10
10
12
14
16
18
20
22
24
constante de tiempo característica teórica [s]
Figura 10. Gráfico que comprueba la definición teórica de la constante de tiempo
característica de un circuito RC.
Conclusión
Las figuras 2 y 3 comprueban la ecuación (3) que dice que la tensión en el capacitor
durante la carga tiende exponencialmente a la tensión de la fuente cuando la carga del mismo tiende
a la carga máxima. En las figuras 6 y 7 se puede ver la caída exponencial de la tensión en el
capacitor cuando éste se descarga hasta llegar a una tensión igual a cero.
De los datos y la relación dada en la ecuación (8) pudimos obtener el valor de las
constantes de tiempo características de los circuitos, para distintas resistencias. De las figuras 4, 5, 8
y 9, y a partir de la regresión lineal, obtuvimos el valor de τ de la pendiente de las rectas.
Pudimos comprobar que para resistencias mayores, la constante de tiempo característica
del circuito resulta mayor.
Además, se comprueba en la figura 10 la definición de la constante característica τ dada
en la ecuación (4), ya que la pendiente que obtuvimos fue de 1,00 ± 0,03 de graficar los valores de τ
obtenidos experimentalmente en función del producto de las resistencias R usadas en cada caso y el
capacitor C utilizado de 10µF.
Los experimentos realizados comprobaron con gran aproximación a la teoría conocida
sobre circuitos RC que describe su comportamiento durante la carga y la descarga de un capacitor.
Bibliografía
(1)
Física Universitaria, F. W. Sears, M. W. Zemansky y H. D. Young, 6ta. Ed., Editorial Fondo Educativo
Interamericano, México (1986).
(2)
Física Re-Creativa, S. Gil y E. Rodriguez, 1ra. Ed., Argentina (2000).
Carga y descarga de capacitores- M.P. Frigerio,G. La Bruna,M.G. Larreguy y J. Romani - UF 2001
6