Fórmulas para flexión simple: sección constante
Anuncio
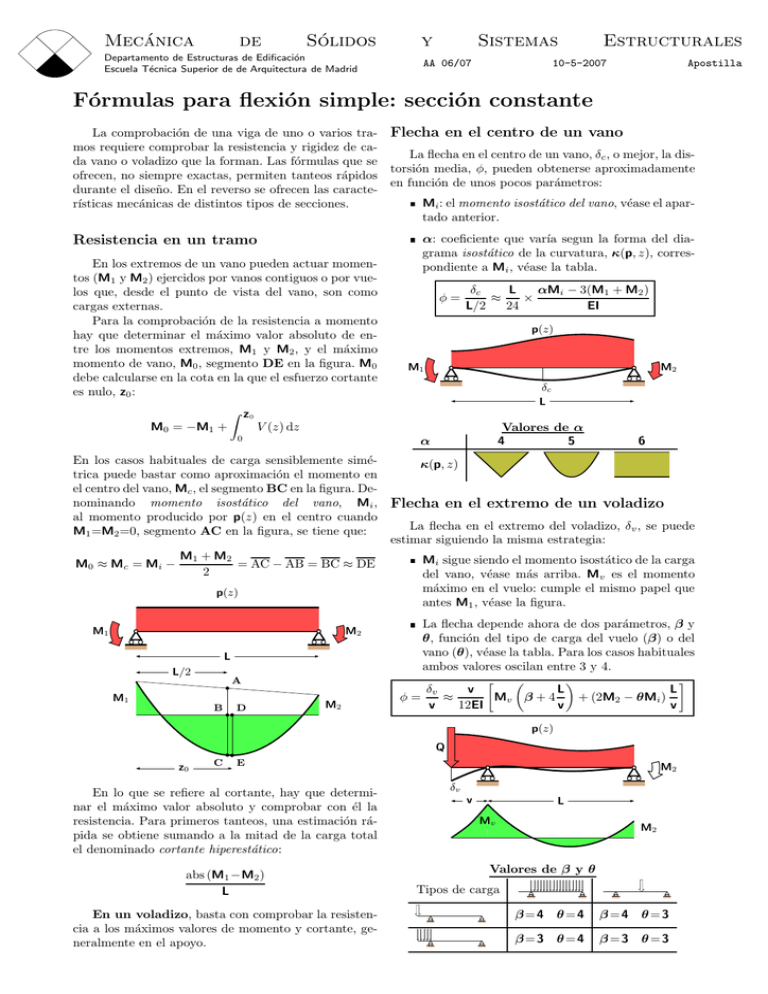
Mecánica de Sólidos Departamento de Estructuras de Edificación Escuela Técnica Superior de de Arquitectura de Madrid y Sistemas AA 06/07 Estructurales 10-5-2007 Apostilla Fórmulas para flexión simple: sección constante La comprobación de una viga de uno o varios tra- Flecha en el centro de un vano mos requiere comprobar la resistencia y rigidez de caLa flecha en el centro de un vano, δc , o mejor, la disda vano o voladizo que la forman. Las fórmulas que se torsión media, φ, pueden obtenerse aproximadamente ofrecen, no siempre exactas, permiten tanteos rápidos en función de unos pocos parámetros: durante el diseño. En el reverso se ofrecen las caracteMi : el momento isostático del vano, véase el aparrı́sticas mecánicas de distintos tipos de secciones. tado anterior. Resistencia en un tramo En los extremos de un vano pueden actuar momentos (M1 y M2 ) ejercidos por vanos contiguos o por vuelos que, desde el punto de vista del vano, son como cargas externas. Para la comprobación de la resistencia a momento hay que determinar el máximo valor absoluto de entre los momentos extremos, M1 y M2 , y el máximo momento de vano, M0 , segmento DE en la figura. M0 debe calcularse en la cota en la que el esfuerzo cortante es nulo, z0 : M0 = −M1 + Z z0 L αMi − 3(M1 + M2 ) δc ≈ × L/2 24 EI p(z) M1 M2 δc L p(z) M1 M2 L L/2 A M1 D Valores de α 4 5 α M 1 + M2 = AC − AB = BC ≈ DE 2 B φ= V (z) dz 0 En los casos habituales de carga sensiblemente simétrica puede bastar como aproximación el momento en el centro del vano, Mc , el segmento BC en la figura. Denominando momento isostático del vano, Mi , al momento producido por p(z) en el centro cuando M1 =M2 =0, segmento AC en la figura, se tiene que: M 0 ≈ M c = Mi − α: coeficiente que varı́a segun la forma del diagrama isostático de la curvatura, κ(p, z), correspondiente a Mi , véase la tabla. M2 6 κ(p, z) Flecha en el extremo de un voladizo La flecha en el extremo del voladizo, δv , se puede estimar siguiendo la misma estrategia: Mi sigue siendo el momento isostático de la carga del vano, véase más arriba. Mv es el momento máximo en el vuelo: cumple el mismo papel que antes M1 , véase la figura. La flecha depende ahora de dos parámetros, β y θ, función del tipo de carga del vuelo (β) o del vano (θ), véase la tabla. Para los casos habituales ambos valores oscilan entre 3 y 4. v δv L L ≈ φ= Mv β + 4 + (2M2 − θMi ) v 12EI v v p(z) Q z0 C E En lo que se refiere al cortante, hay que determinar el máximo valor absoluto y comprobar con él la resistencia. Para primeros tanteos, una estimación rápida se obtiene sumando a la mitad de la carga total el denominado cortante hiperestático: abs (M1 −M2 ) L En un voladizo, basta con comprobar la resistencia a los máximos valores de momento y cortante, generalmente en el apoyo. M2 δv v L Mv M2 Valores de β y θ Tipos de carga β=4 θ=4 β =4 θ=3 β=3 θ=4 β =3 θ=3 c 2007, Vázquez. Printed with free software: GNU/Linux/emacs/LATEX 2ε /Postscript. Copyleft (1) A I I/I2 W W/W2 AR z/h Wp /W S (2) (3) (4) (5) (6) (7) (8) (9) (10) Ah2 /4 Ah/2 0,25Ah2 h2 3 A 0, 5Ah h 3√ A 0 1 1 Ah 4 0, 25Ah 1,5A2 ≈ 2,5A2 3,2A2 15 ≈ 30 40 0,95A3/2 ≈ 1,28A3/2 1,43A3/2 6,5 ≈ 8,0 9 0,32A ≈ 0,33A 0,36A A/2 z ideal h=z A/2 b h bmin bmin ≈ 0,03h IPE pequeño mediano grande bmin bmin ≈ 0,04h b HEB pequeño mediano grande h/3,3 ≈ h/4 h/4,5 A h2 /10 ≈ h2 /15 h2 /20 ≈ Ah2 /6 h/2,2 ≈ h/2,5 h/2,8 h2 /5 ≈ h2 /6 h2 /8 Cualquier HEB: proporción h λ= b h A Cualquier IPE: b h √ √ bh bh 0,98A2 ≈ 1,15A2 1,54A2 ≈ Ah/3 11 ≈ 14 17 0,86A3/2 ≈ 0,93A3/2 1,09A3/2 ' 2Ah2 /11 ' 4Ah/11 bh3 /12 bh2 /6 2 λA /12 λ √ λA 3/2 /6 ≈ A/3 4,8 ≈ 5,4 6 λ ' 8/9 ' 1,14 ' 8/9 ' 1,13 Ah2 /12 h h2 0,083h4 1 0,167h3 1 0,67h2 πh/2 0,89h πh2 /4 0,79h2 πh4 /64 A2 /4π 3/π πh3 /32 √ A3/2 /4 π √ 3/2 π 3πh2 /16 0,589h2 2A/3 6 Ah 29 ' 0,206Ah 1 Ah 8 0,67A h2 /λ 5 Ah 26 ' 0,192Ah ' 2bh/3 √ h/ λ Ah/6 ' 0,22A ≈ 0,20A 0,24A ≈ A/5 √ 1 0,67 1,5 h λ=1 h d h=d h h h a h = 1,41a √ a 0.71h a2 h2 /2 Ah2 /16 a4 /12 A2 /12 Ah2 /24 0,964 1 Ah/8 √ a3 /6 2 √ A3/2 /6 2 Ah/12 0,846 0,71 3A/4 8a2 /9 0,444h2 8A/9 0,125Ah 3π/16 0,589 0,5 1,70 1 Ah 3π 0,106Ah 2 1 Ah 12 0,083Ah Constantes mecánicas para la flexión en un plano vertical respecto al centro de gravedad de la sección. H, I 2 y W2 : respectivamente, canto, inercia y módulo resistente de la sección cuadrada de igual área que la sección considerada. AR : área eficaz a esfuerzo cortante y rasante. Wp : módulo resistente de la sección plastificada (con curvatura infinita); la reserva plástica no puede utilizarse en su totalidad cuando W p /W es mayor que el coeficiente de seguridad aplicable, γ; en el análisis plástico de estructuras de acero, γ suele ser 1,12 veces mayor que en análisis elástico. S: momento estático de media sección. Los valores para perfiles IPE y HEB son aproximados y deben comprobarse los diseños con los catálogos del fabricante. ‘'’ denota una aproximación muy buena (errores por debajo del 5 %); ‘≈’ denota una aproximación decente. Un perfil puede considerarse pequeño si su canto es menor que 220 mm; y grande, si es mayor que 330 mm. La tensión tangencial máxima en un rombo se produce a un octavo del canto por encima y por debajo del centro de gravedad. Secciones para flexión simple. H Tipo de sección


