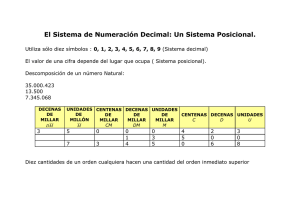
Para escribir los números, empleamos los siguientes signos:
Anuncio

PLANEACIÓN DEL TERCER BIMESTRE PLANEACIÓN DEL TERCER BIMESTRE ASIGNATURA: MATEMÁTICAS TEMA: NOMBRE Y ESCRITURA DE NUMEROS APRENDIZAJE ESPERADO: COMPARAR Y ORDENAR NÚMEROS NATURALES DE CUATRO CIFRAS A PARTIR DE SUS NOMBRES O DE SU ESCRITURA CON CIFRAS. CONTENIDO CIENTÍFICO: Para escribir los números, empleamos los siguientes signos: Estos signos se llaman cifras o guarismos. Nuestro sistema de numeración es decimal, porque tiene como base el número diez. 10 unidades simples forman = 1 decena 10 decenas forman= 1 centena 10 centenas forman = 1 unidad de milla 10 unidades de millar forman = 1 decena de millar 10 decenas de millar forman = 1 centena de millar Cada una de las unidades ocupa un lugar determinado en los números. , el tercer lugar Así las unidades simples ocupan el primer lugar de la derecha, el segundo lugar; las centenas, etcétera, como el siguiente cuadro: En el cuadro anterior, 4 es unidad de primer orden, 3 es unidad de segundo orden, etc. EJEMPLO: 6° 5° 4° 3° 2° 1° Orden Centenas de millar Decenas de millar Unidades de millar Centenas Decenas Unidades Nombre 1 0 5 7 3 4 ACTIVIDAD: Escribe 140: 38055: 222402: con letra las siguientes cantidades: 375: 90002: 800080: EVALUACIÓN. Verificar que la ubicación de las fracciones en las rectas se correcta y evaluar el apunte completo. ASIGNATURA: MATEMÁTICAS TEMA: USO DE LOS SIGNOS > Y < APRENDIZAJE ESPERADO: COMPARA Y ORDENA NÚMEROS NATURALES DE CUATRO CIFRAS A PARTIR DE SUS NOMBRES O DE SU ESCRITURA CON CIFRAS. CONTENIDO CIENTÍFICO: Una cifra diferente de cero tiene dos valores : VALOR ABSOLUTO: es el que tiene por su figura. VALOR POSICIONAL: es el que adquiere por la posición que ocupa en el número El valor posicional de las cifras que forman dos números determina cuál es el mayor y cuál el menor. En el número 44 444 todas las cifras tienen el mismo valor absoluto: 4. Los valores posicionales seria de la siguiente manera: 4 unidades = 4 unidades 4 decenas = 40 unidades 4 centenas = 400 unidades 4 unidades de millar = 4 000 unidades 4 decenas de millar = 40 000 unidades EJEMPLO: ACTIVIDAD: Comparar una serie de números utilizando los signos >, < o igual NÚMERO O < 1870 < NÚMERO EL NÚMERO MENOR ES… 1900 MIL OCHOCIENTOS SETENTA. EVALUACIÓN. VERIFICAR QUE LOS RESULTADOS SEAN CORRECTOS PASANDO AL PIZARRÓN A LOS ALUMNO A DAR SOLUCIÓN A CADA UNO DE LAS OPERACIONES, ASÍ COMO TAMBIÉN REVISAR LA ORTOGRAFÍA Y CONTENIDO COMPLETO. PLANEACIÓN DEL TERCER BIMESTRE ASIGNATURA: MATEMÁTICAS TEMA: EXPRESIONES ADITIVAS Y MULTIPLICATIVAS APRENDIZAJE ESPERADO: IDENTIFICAR EXPRESIONES ADITIVAS, MULTIPLICATIVAS Y MIXTAS QUE SON EQUIVALENTES, Y SE UTILIZAN AL EFECTUAR CÁLCULOS CON NÚMEROS NATURALES. CONTENIDO CIENTÍFICO: Los números naturales y decimales se pueden expresar como una descomposición aditiva, multiplicativa o mixta. EJEMPLO: NÚMERO 25 0.75 SUMADOS MULTIPLICACIÓN 5+5+5+5+5 5X5 0.25+0.25+0.25 0.25X3 MIXTA 5X4+5 0.25X2+0.25 ACTIVIDAD: Proporcionar al alumno una imagen en donde tendrán que colorear de acuerdo a la clave que se escriba en el pizarrón EVALUACIÓN. VERIFICAR QUE LOS RESULTADOS SEAN CORRECTOS PASANDO AL PIZARRÓN A LOS ALUMNO A DAR SOLUCIÓN A CADA UNO DE LAS OPERACIONES, ASÍ COMO TAMBIÉN REVISAR LA ORTOGRAFÍA Y CONTENIDO COMPLETO. PLANEACIÓN DEL TERCER BIMESTRE ASIGNATURA: MATEMÁTICAS TEMA: FRACCIONES EQUIVALENTES EN REPARTO Y MEDICIÓN APRENDIZAJE ESPERADO: RESOLLVER PROBLEMAS ADITIVOS CON NUMEROS FRACCIONARIOS O DECIMALES, EMPLEANDO LOS ALGORITMOS CONVENCIONALES. CONTENIDO CIENTÍFICO: Las Fracciones Equivalentes tienen el mismo valor, aunque parezcan diferentes. ¿Por qué son lo mismo? Porque cuando multiplicas o divide a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es: ¡Lo que haces a la parte de arriba de la fracción también lo tienes que hacer a la parte de abajo! Y en un dibujo se ve así: 1 /2 2 /4 4 /8 = = Si seguimos dividiendo hasta que no podamos más, habremos simplificado la fracción (la hemos hecho la más simple posible). Importante: Las partes de arriba y abajo de la fracción siempre deben ser números enteros. Las operaciones que podemos hacer son multiplicar y dividir (siempre las dos partes a la vez). Si sumamos o restamos un número arriba y abajo, no tendremos una fracción equivalente. El número que elijas para dividir las dos partes no debe dejar ningún resto en las divisiones. EJEMPLO: ACTIVIDAD: PROPORCIONAR UNA COPIA EN EL CUAL LOS ALUMNOS TENDRAN QUE IDENTIFICAR EN BASE A LAS IMÁGENES LAS FRACCIONES EQUIVALENTES. EVALUACIÓN. VERIFICAR QUE LOS RESULTADOS SEAN CORRECTOS PASANDO AL PIZARRÓN A LOS ALUMNO A DAR SOLUCIÓN A CADA UNO DE LAS OPERACIONES, ASÍ COMO TAMBIÉN REVISAR LA ORTOGRAFÍA Y CONTENIDO COMPLETO.