1.- Se observa que los datos están más dispersos conforme
Anuncio
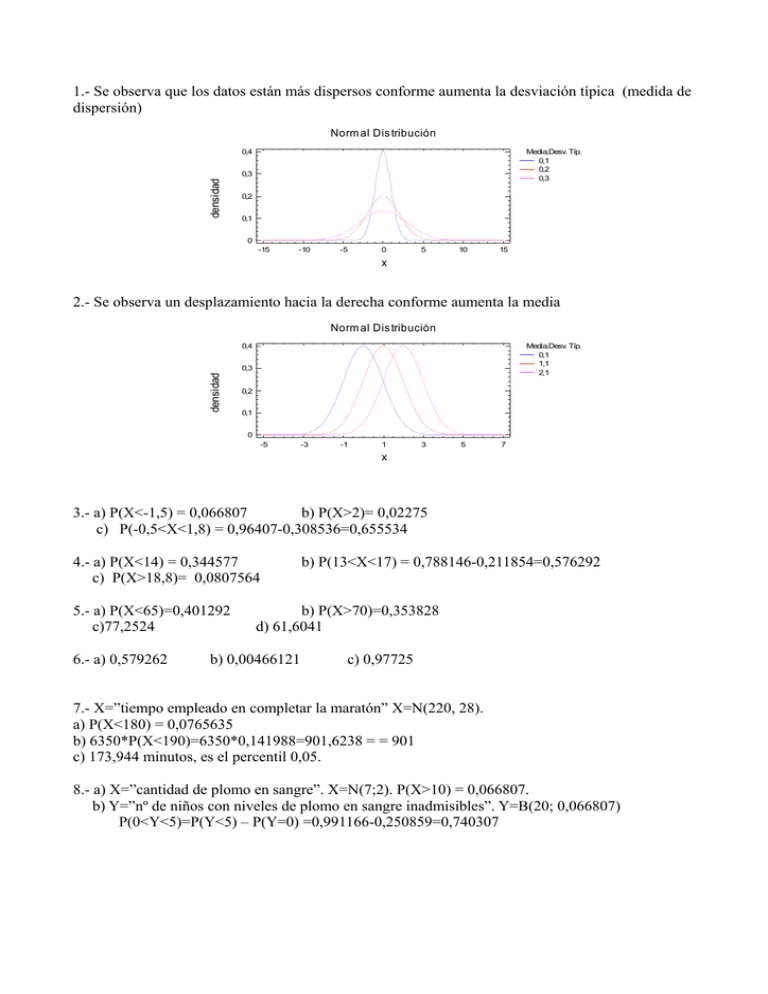
1.- Se observa que los datos están más dispersos conforme aumenta la desviación típica (medida de dispersión) Norm al Dis tribución 0,4 Media,Desv. Típ. 0,1 0,2 0,3 densidad 0,3 0,2 0,1 0 -15 -10 -5 0 5 10 15 x 2.- Se observa un desplazamiento hacia la derecha conforme aumenta la media Norm al Dis tribución 0,4 Media,Desv. Típ. 0,1 1,1 2,1 densidad 0,3 0,2 0,1 0 -5 -3 -1 1 3 5 7 x b) P(X>2)= 0,02275 3.- a) P(X<-1,5) = 0,066807 c) P(-0,5<X<1,8) = 0,96407-0,308536=0,655534 4.- a) P(X<14) = 0,344577 c) P(X>18,8)= 0,0807564 5.- a) P(X<65)=0,401292 c)77,2524 6.- a) 0,579262 b) P(13<X<17) = 0,788146-0,211854=0,576292 b) P(X>70)=0,353828 d) 61,6041 b) 0,00466121 c) 0,97725 7.- X=”tiempo empleado en completar la maratón” X=N(220, 28). a) P(X<180) = 0,0765635 b) 6350*P(X<190)=6350*0,141988=901,6238 = = 901 c) 173,944 minutos, es el percentil 0,05. 8.- a) X=”cantidad de plomo en sangre”. X=N(7;2). P(X>10) = 0,066807. b) Y=”nº de niños con niveles de plomo en sangre inadmisibles”. Y=B(20; 0,066807) P(0<Y<5)=P(Y<5) – P(Y=0) =0,991166-0,250859=0,740307 9.- a) X=”peso de un comprimido fabricado en A” X=N(746;15). P(751<X<760) = 0,824677- 0,630561=0,194116 b) Definimos Y=”peso de un comprimido fabricado en B” Y=N(754;22). Casos favorables/casos posibles =P(A y X>745) / P(X>745) P(A y peso>745)= P(A)P(peso>745 | A) P(peso>745) = P(A y peso>745)+P(B y peso>745) P(fabricado en A)=P(A)=0,65; P(fabricado en B)=P(B)=0,35 P(peso>745 | fabricado en A) = P(peso>745 | A) = P(X>745)=0,526579 P(peso>745 | fabricado en B) = P(peso>745 | B) = P(Y>745)= 0,658765 Por la fórmula de Bayes, P(A | peso>745) = P(A)*P(peso>745 | A)/(P(A)*P(peso>745 | A)+P(B)*P(peso>745 | B))= = (0,65 * 0,526579)/(0,65 * 0,526579 + 0,35 * 0,658765) = 0,597503491788 = 0,5975 10.- En ambos casos se observa una gran semejanza. 10.1 Normal Distribución Binomial Distribución 0,08 densidad probabilidad Media,Desv. T 30,4,58 0,1 Prob. de Even 0,3,100 0,1 0,08 0,06 0,04 0,06 0,04 0,02 0,02 0 0 0 0 20 40 60 80 10 20 100 30 40 50 60 x x 10.2 Normal Distribución Normal Distribución 0,04 densidad densidad 0,04 0,03 0,02 0,02 0 0 0 20 40 60 80 100 120 x a) 0,689186 c) 0,9999 0,03 0,01 0,01 11.- Media,Desv. T 64,8 0,05 Media,Desv. T 64,8 0,05 b) 0,832219-0,38446 = 0,447759 d) 0,998415-0,469613=0,528802 0 20 40 60 x 80 100 120 12.- a) 0,817258 b) 0,892398-0,00542178= 0,88697622 13.- Para generar una lista aleatoria de datos que provenga de una distribución normal con parámetros mu y sigma: Descripción-->Distribuciones--> Distribuciones de probabilidad-->Normal. Introduce los valores de mu y sigma. Opciones tabulares (botón amarillo)-->Números aleatorios. En Guardar resultados (botón azul o ver nuevo marco)--> Ir a la tabla de entrada de datos.










