Tabla de Reglas Derivadas
Anuncio
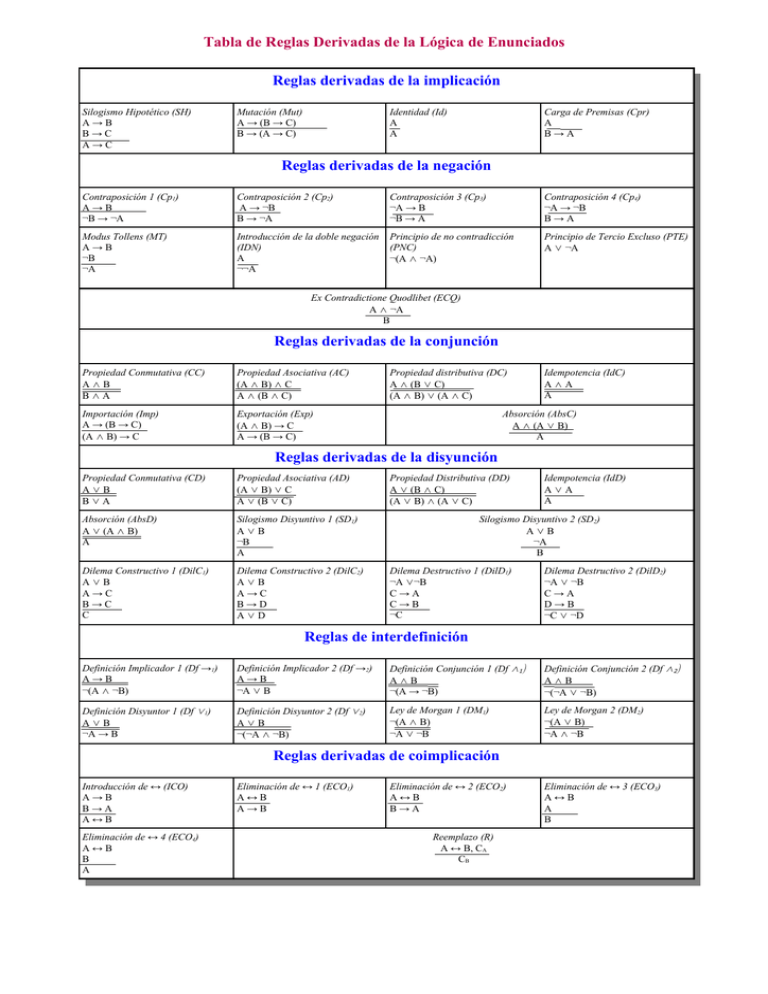
Tabla de Reglas Derivadas de la Lógica de Enunciados Reglas derivadas de la implicación Silogismo Hipotético (SH) A→B B→C A→C Mutación (Mut) A → (B → C) B → (A → C) Identidad (Id) A A Carga de Premisas (Cpr) A B→A Reglas derivadas de la negación Contraposición 1 (Cp1) A→B ¬B → ¬A Contraposición 2 (Cp2) A → ¬B B → ¬A Contraposición 3 (Cp3) ¬A → B ¬B → A Contraposición 4 (Cp4) ¬A → ¬B B→A Modus Tollens (MT) A→B ¬B ¬A Introducción de la doble negación (IDN) A ¬¬A Principio de no contradicción (PNC) ¬(A ∧ ¬A) Principio de Tercio Excluso (PTE) A ∨ ¬A Ex Contradictione Quodlibet (ECQ) A ∧ ¬A B Reglas derivadas de la conjunción Propiedad Conmutativa (CC) A∧B B∧A Propiedad Asociativa (AC) (A ∧ B) ∧ C A ∧ (B ∧ C) Importación (Imp) A → (B → C) (A ∧ B) → C Exportación (Exp) (A ∧ B) → C A → (B → C) Propiedad distributiva (DC) A ∧ (B ∨ C) (A ∧ B) ∨ (A ∧ C) Idempotencia (IdC) A∧A A Absorción (AbsC) A ∧ (A ∨ B) A Reglas derivadas de la disyunción Propiedad Conmutativa (CD) A∨B B∨A Propiedad Asociativa (AD) (A ∨ B) ∨ C A ∨ (B ∨ C) Absorción (AbsD) A ∨ (A ∧ B) A Silogismo Disyuntivo 1 (SD1) A∨B ¬B A Dilema Constructivo 1 (DilC1) A∨B A→C B→C C Dilema Constructivo 2 (DilC2) A∨B A→C B→D A∨D Propiedad Distributiva (DD) A ∨ (B ∧ C) (A ∨ B) ∧ (A ∨ C) Idempotencia (IdD) A∨A A Silogismo Disyuntivo 2 (SD2) A∨B ¬A B Dilema Destructivo 1 (DilD1) ¬A ∨¬B C→A C→B ¬C Dilema Destructivo 2 (DilD2) ¬A ∨ ¬B C→A D→B ¬C ∨ ¬D Reglas de interdefinición Definición Implicador 1 (Df →1) A→B ¬(A ∧ ¬B) Definición Implicador 2 (Df →2) A→B ¬A ∨ B Definición Conjunción 1 (Df ∧1) A∧B ¬(A → ¬B) Definición Conjunción 2 (Df ∧2) A∧B ¬(¬A ∨ ¬B) Definición Disyuntor 1 (Df ∨1) A∨B ¬A → B Definición Disyuntor 2 (Df ∨2) A∨B ¬(¬A ∧ ¬B) Ley de Morgan 1 (DM1) ¬(A ∧ B) ¬A ∨ ¬B Ley de Morgan 2 (DM2) ¬(A ∨ B) ¬A ∧ ¬B Reglas derivadas de coimplicación Introducción de ↔ (ICO) A→B B→A A↔B Eliminación de ↔ 4 (ECO4) A↔B B A Eliminación de ↔ 1 (ECO1) A↔B A→B Eliminación de ↔ 2 (ECO2) A↔B B→A Reemplazo (R) A ↔ B, CA CB Eliminación de ↔ 3 (ECO3) A↔B A B