Tema 5: Circuitos secuenciales

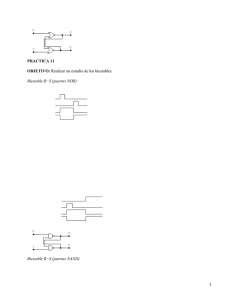
Estructura de computadores
Tema 5:
Tema 5: Sistemas secuenciales
Circuitos secuenciales
5.1 Introducción: tablas de transición, cronogramas.
Hemos visto como en los circuitos combinacionales, las salidas sólo
dependen de las entradas en el mismo instante de tiempo. Existe otro tipo de
circuitos digitales en los cuales esto no es así. Son los llamados circuitos o
sistemas secuenciales.
Circuitos secuenciales
Son aquellos en los cuales las salidas en un instante de tiempo
determinado dependen de las entradas en ese instante y en instantes
anteriores de tiempo.
Como consecuencia de la definición anterior podemos llegar a la
conclusión de que este tipo de circuitos son capaces de memorizar información
y que esta información en un momento dado depende de las entradas
ocurridas en el circuito hasta ese momento.
El circuito no es capaz de memorizar todas las entradas ocurridas hasta
un instante de tiempo determinado, sino solo una cierta parte. A la información
almacenada se le denomina estado del sistema, y el número máximo de
informaciones almacenables es el número de estados posibles del sistema.
El diagrama de bloques de un circuito secuencial es:
E
S
Q(t)
Circuito
combinacional
Q(t+1)
Elementos de
almacenamiento
El circuito secuencial recibe información binaria de su ambiente a través
de las entradas E, las cuales, en combinación con el estado actual Q(t)
(almacenado en los elementos de almacenamiento), determinan el valor binario
de las salidas S y el siguiente estado Q(t+1).
Las salidas de un circuito secuencial son las salidas del circuito
combinacional.
1
Estructura de computadores
Tema 5: Sistemas secuenciales
5.1.1 Funciones de transición
Un circuito o sistema secuencial queda definido por dos funciones
lógicas, llamadas funciones de transición:
1. Función de salida: nos indica cómo depende la salida o salidas, de
las entradas actuales y del estado actual.
2. Función de transición de estado: nos indica como depende el
nuevo estado del estado anterior y de las entradas al sistema.
5.1.1.1 Función de salida
Si designamos por:
S(t) = salidas en el mismo instante de tiempo t
E(t) = entradas en el mismo instante de tiempo t
Q(t) = estado en el instante de tiempo t
La función de salida puede expresarse:
S (t) = F [ E (t), Q (t) ]
5.1.1.2 Función de transición de estado
Nos indica si unas determinadas entradas producen un cambio en el
estado y a qué estado se cambia. La función puede expresarse:
Q(t+1) = G [ E(t), Q(t) ]
Tanto F como G son funciones lógicas, exactamente iguales a las
estudiadas hasta ahora. La única novedad, que confiere a los circuitos
secuenciales propiedades totalmente distintas a los combinacionales, es el
hecho de que existe realimentación. La función G nos da los valores Q en
función de los propios valores Q anteriores. Las mismas variables son variables
de entrada y salida de la función.
Las funciones F y G pueden expresarse mediante tablas de verdad.
como cualquier otra función. Por el hecho de existir realimentación, se les
denomina tablas de transición del circuito secuencial.
5.1.2 Cronogramas
Hemos visto que los circuitos secuenciales tienen una estructura tal que
las salidas dependen del tiempo, ya que el estado depende de las entradas y
éstas son función del tiempo.
Aunque las tablas de transición permiten definir un circuito secuencial,
cuando éste es complejo, es más cómodo manejar una representación gráfica
de las variables en función del tiempo. A esta representación se le llama
cronograma.
Más adelante veremos los cronogramas de los distintos biestables.
2
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2 Biestables
Los biestables son circuitos lógicos capaces de permanecer en uno de
entre dos estados estables, aún después de desaparecer la causa que provocó
el paso al estado alcanzado. Son, pues, capaces de almacenar una
información binaria (1 bit).
5.2.1 Tipos de biestables.
Deben distinguirse tres aspectos en las señales de entrada que
producen la transición de un estado a otro:
1. La lógica de disparo, que determinará que el biestable cambie de
estado cuando en sus entradas se dé una cierta combinación de
señales. Es el modo de funcionamiento. Puede haber tantos
biestables como lógicas de cambio nos imaginemos. En la práctica
sólo se usan 4 tipos de biestables.
2. El tipo de disparo, que determinará la forma en que las excitaciones
de entrada afectan al estado del biestable.
3. El sincronismo en el disparo, que determinará si el funcionamiento
del biestable se hará de acuerdo con la presencia de una señal
adicional a las entradas, y que se denomina señal de reloj.
Combinando estos tres aspectos, los fabricantes han comercializado una
gran variedad de biestables, que son suficientes para las necesidades de
diseño. Podemos clasificar los biestables según estos criterios.
1. Atendiendo a la lógica de disparo (modo de funcionamiento):
q Biestables R-S
q Biestables J-K
q Biestables D
q Biestables T
2. Atendiendo al sincronismo en el disparo y tipo de disparo:
q Asíncronos (latches): funcionan sin señal de reloj.
q Síncronos (flip-flops): funcionan con señal de reloj.
§
Disparo por nivel de tensión: alto ("1") o bajo ("0")
§ Nivel alto ("1"): El biestable podrá cambiar de estado
cuando la señal de reloj esté a "1".
§ Nivel bajo ("0"): El biestable podrá cambiar de estado
cuando la señal de reloj esté a "0".
§
Disparo por flanco: de subida o bajada
§ Flanco de subida: El biestable podrá cambiar de estado en
el instante en que la señal de reloj pase de "0" a "1".
§ Flanco de bajada: El biestable podrá cambiar de estado en
el instante en que la señal de reloj pase de "1" a "0".
3
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.1.1 Biestables asíncronos (latches)
Asíncronos quiere decir que funcionan sin señal de reloj; cualquier
cambio en las entradas produce un cambio en las salidas, en cualquier
momento. En el caso de tener varios biestables asíncronos en un circuito, cada
uno actuaría de forma independiente a los otros.
5.2.1.2 Biestables síncronos (flip-flops)
Son los que funcionan en sincronismo con una señal de reloj. A estos
también se les llama circuitos secuenciales sincronizados, y son el tipo de
circuito más utilizados en la práctica, ya que son relativamente sencillos de
diseñar.
Un circuito secuencial síncrono emplea señales que afectan los
elementos de almacenamiento sólo a instantes discretos de tiempo. La
sincronización se logra por medio de un dispositivo de sincronía, llamado
generador de reloj, que produce un tren periódico de pulsos de reloj, a
intervalos fijos.
Esto significa que en los biestables síncronos, la tabla de transición solo
se cumple cuando se activa la señal de reloj. Si la señal de reloj no se activa,
no se produce ninguna transición. Por tanto, aunque en las entradas haya una
combinación de señales que conduzcan a una transición de estado, ésta no se
producirá hasta que se active la señal de reloj, y no volverá a producirse una
nueva transición hasta que se active de nuevo la señal de reloj.
La señal de reloj puede activarse de dos formas: por nivel o por flanco.
5.2.1.2.1 Biestables activados por nivel (de tensión):
Un biestable activado por nivel podrá cambiar de estado cuando la
señal de reloj esté a un determinado nivel de tensión: "1" (nivel alto) o "0" (nivel
bajo).
Nivel alto
Nivel bajo
5.2.1.2.2 Biestables activados por flanco:
Un biestable activado por flanco ignora el pulso de reloj mientras está
en un nivel constante y se dispara sólo durante una transición de la señal de
reloj, de "0" a "1" (flanco de subida) o de "1" a "0" (flanco de bajada).
Reloj
Reloj
t
Flanco de subida
t
Flanco de bajada
4
Estructura de computadores
Tema 5: Sistemas secuenciales
El diseño de circuitos asíncronos complejos es más difícil que el de
circuitos síncronos, puesto que su comportamiento depende en gran medida de
los retardos de propagación de las puertas lógicas y de la sincronía de los
cambios de las entradas.
De todas formas, siempre se necesita algo de diseño asíncrono, ya que:
1. los latches (elementos de almacenamiento en circuitos asíncronos)
se utilizan como bloques de construcción de los flip-flops
(elementos de almacenamiento en circuitos síncronos).
2. Los biestables (flip-flops) que vamos a estudiar decimos que tienen
entradas síncronas, ya que los datos se transfieren sincronizados con
la señal de reloj, sólo durante el flanco de disparo del pulso de reloj.
Pero la mayoría de los IC disponibles en el mercado presentan
también entradas asíncronas, las cuales pueden cambiar el estado
del flip-flop independientemente del reloj. Estas entradas pueden ser
por nivel alto ("1") o por nivel bajo ("0") y son prioritaras sobre las
otras señales de entrada. Podemos tener las siguientes:
• Inicialización o Preset (PRE): pone al biestable en estado SET
("1").
• Borrado o Clear (CLR): pone al biestable en estado RESET ("0").
En su forma más elemental, un biestable consiste en dos inversores
interacoplados (realimentados), la salida de uno conectada a la entrada del otro
y viceversa, como se ve en la figura:
1
0
0
1
0
1
1
0
Este circuito es capaz de estar en dos estados estables, pero para
cambiar de estado, hay que actuar sobre las salidas, por lo que no es útil.
Se requiere un circuito de entrada, separado del de salida. Además, se
necesita que el biestable responda a una lógica de disparo, es decir, cambie de
estado según un criterio preestablecido fijo.
Ahora vamos a estudiar los 4 tipos básicos de biestables: R-S, J-K, D y
T, estudiando su tabla de de transición, circuito y cronograma, tanto para el
caso de que funcionen asíncronamente (sin señal de reloj) como
síncronamente (con señal de reloj). Veremos los casos en que la señal de reloj
se activa por nivel (alto/bajo) o por flanco (subida/bajada).
5
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.2 Biestable R-S (latch)
El único biestable que tiene sentido como asíncrono es el R-S. Los
demás requieren reloj para un correcto funcionamiento.
Este biestable tiene dos entradas:
• R (Reset): permite poner a 0 el estado del biestable.
• S (Set): permite ponerlo a 1.
Tiene dos salidas complementarias: Q y Q'. Para analizar la tabla de
transición basta con que nos fijemos en Q.
La tabla de transición es la siguiente, en forma normal y forma
compacta:
R
0
0
0
0
1
1
1
1
S
0
0
1
1
0
0
1
1
Q(t) Q(t+1)
0
0
1
1
0
1
1
1
0
0
1
0
0
ND
1
ND
R
0
0
1
1
S
0
1
0
1
Q(t+1)
Q(t)
1
0
ND
Comentario
No cambia
Se activa Set
Se activa Reset
No Definido
ND = No definido
En el último caso, el hecho de que el nuevo estado no está definido no
quiere decir que el biestable se deteriore si R=S=1. Lo que significa es que no
podemos predecir en qué estado quedará.
El símbolo como bloque del biestable R-S es el siguiente:
R
Q
R'
Q
S
Q'
S'
Q'
y el circuito puede ser implementado con sólo dos puertas NOR con
acoplamiento cruzado y con entrada activa a nivel alto o con dos puertas NAND
con entrada activa a nivel bajo:
R
S
Q
Q'
R'
S'
Q
Q'
En el caso de utilizar puertas NAND, las órdenes Reset y Set suceden
para entradas a nivel bajo (0); en este caso, el biestable se llama biestable
R'S', y su tabla de verdad es todo invertido (R=S=0 no permitido, etc.)
6
Estructura de computadores
Tema 5: Sistemas secuenciales
Vamos a explicar el funcionamiento del biestable R-S (latch) con el
primer circuito (con puertas NOR). Lo que hacemos es cambiar los valores de
las dos entradas R y S y observaremos las señales de salida Q y Q'.
R
S
1
Q
2
Q'
Suponemos que R=S=Q=0 (nivel bajo). Dado que la salida Q se
realimenta a una entrada de la puerta 2 y su otra entrada es S=0, la salida de la
puerta 2 tiene que ser Q'=1. Pero esta salida está acoplada de nuevo a una
entrada de la puerta 1, asegurando así que su salida sea Q=0, es decir, el
biestable no cambia de estado.
Cuando la salida Q esté a nivel bajo (Q=0), el latch se encuentra en
estado RESET ("0") y permanecerá indefinidamente en él hasta que se le
aplique un nivel alto en la entrada S (S=1). Al tener S=1, la salida de la puerta 2
se pone a nivel bajo (Q'=0). Como tenemos que R=0 y Q'=0, la salida de la
puerta 1 se pone a nivel alto (Q=1). Este nivel alto en la salida Q se realimenta
a una de las entradas de la puerta 2, asegurando que su salida Q' permanece a
nivel bajo (Q'=0) incluso cuando se elimine el nivel alto de la entrada S (S=0).
Cuando la salida Q esté a nivel alto (Q=1), el latch se encuentra en
estado SET ("1"), y permanecerá indefinidamente en él hasta que se le aplique
un nivel alto en la entrada R (R=1).
Si estando en este estado SET (Q=1), eliminamos simultánemente los
niveles altos de las dos entradas (R=S=0), como la salida Q se realimenta en
una entrada de la puerta 2, y la otra entrada es S=0, su salida estará a nivel
bajo (Q'=0). Como esta salida está acoplada de nuevo a una entrada de la
puerta 1, y la otra entrada es R=0, su salida estará a nivel alto (Q=1). Vemos
que el biestable no cambia de estado.
En operación normal, las salidas de un latch (Q y Q') son siempre
complementarias una de la otra. Sin embargo, se produce una condición de
funcionamiento no válida en un biestable R-S cuando se aplican
simultáneamente niveles altos a las dos entradas R y S (R=S=1). En esta
situación, las dos salidas deberían estar forzósamente a nivel bajo (Q=Q'=0), lo
que viola la condición de complementariedad de las salidas.
Además, si se eliminan simultánemente los niveles altos de las dos
entradas (R=S=0), las dos salidas van a tender al nivel alto y, dado que
siempre va a existir un cierto retraso de propagación de la señal eléctrica a
través de las puertas, una de las puertas dominará en la transición a nivel alto
(una de las puertas siempre será más lenta que la otra). Esto hará que la salida
de la puerta más lenta permanezca a nivel bajo. Cuando se produce esta
situación, no se puede predecir el siguiente estado del latch. Si los tiempos
de propagación de las dos puertas fueran exactamente iguales se producirían
oscilaciones 0,1,0,1,...
7
Estructura de computadores
Tema 5: Sistemas secuenciales
Los cronogramas correspondientes a un biestable R-S con puertas
NOR y NAND son los siguientes. Como estamos analizando el biestable como
asíncrono, no dependerá de una señal de reloj, sino de cómo cambiemos las
entradas R y S y del estado anterior. Igual que hemos hecho antes, lo que
hacemos ahora es cambiar los valores de las dos entradas R y S y
observaremos las señales de salida Q y Q'. Los estados de las entradas R y S
los hemos elegido arbitrariamente para realizar los cronogramas, partiendo en
ambos casos de que Q se encuentra a nivel bajo (Q=0).
R
S
Q
Q'
t
Cronograma biestable R-S (puertas NOR)
Mantiene el estado anterior
Estados no definidos
NOTA: La condición R=S=1 origina un modo de funcionamiento no
válido del biestable, lo que es un gran inconveniente en cualquier latch de tipo
RESET-SET.
NOTA: Mientras no se diga lo contrario, de ahora en adelante
supondremos que los tiempos de propagación de las puertas lógicas que
componen los biestables son nulos, con lo cual la respuesta del biestable será
inmediata.
R'
S'
Q
Q'
t
Cronograma biestable R-S (puertas NAND)
Mantiene el estado anterior
NOTA: en este caso, la condición R=S=0 tiene el mismo problema que
antes.
8
Estructura de computadores
Tema 5: Sistemas secuenciales
Este tipo de biestable, y todos los que vamos a ver, pueden tener una
entrada adicional de habilitación (STROBE o ENABLE), que puede activarse
en estado alto ("1") o bajo ("0"). Cuando esta señal está activa, el biestable
funciona (puede cambiar de estado); cuando está inactiva, no funciona.
En el caso del biestable R-S, debemos añadir la siguiente lógica al circuito
para tener dicha entrada de habilitación. El símbolo lógico o de bloques es el
mismo que antes pero añadimos esta entrada de habilitación.
R
Q
EN
Q'
S
El biestable R-S puede funcionar de forma asíncrona (tal como hemos
visto hasta ahora), pero también de forma síncrona, es decir, utilizando una
señal de reloj como entrada de habilitación. Cuando enumeramos los distintos
tipos de biestables, dentro de los síncronos (flip-flops) vimos que la señal de
reloj se podía activar por "nivel" o por "flanco".
Los símbolos lógicos o de bloques de los biestables R-S síncronos
son los siguientes. Todos tienen una entrada adicional de reloj (Clock). En el
caso de los flip-flops disparados por flanco colocamos un triángulo dentro del
bloque en la entrada del reloj. Este triángulo se denomina "indicador de entrada
dinámica". Para distinguir si se activa por flanco de subida o por flanco de
bajada, colocamos un círculo (como los de negación) en la entrada del reloj.
Activados por nivel:
R
Q
Clock
S
R
Q
Clock
Q'
Activado por nivel alto ("1")
S
Q'
Activado por nivel bajo ("0")
Activados por flanco:
R
Q
R
Clock
S
Q
Clock
Q'
Activado por flanco de subida
S
Q'
Activado por flanco de bajada
NOTA: Esta misma nomenclatura se utiliza en el resto de biestables.
9
Estructura de computadores
Tema 5: Sistemas secuenciales
Vamos a analizar ahora los cronogramas correspondientes a estos
cuatro casos. Al tratarse de biestables síncronos, ahora dependerán de una
señal de reloj. Igual que antes, cambiamos las entradas R y S y comprobamos
las señales de salida Q y Q'. Podemos poner los cuatro casos en un sólo
cronograma.
Reloj
R
S
Qna
Qnb
Qfs
Qfb
t
Cronograma biestables R-S (síncronos)
Donde:
Qna = Salida biestable activado por nivel alto ("1")
Qnb = Salida biestable activado por nivel bajo ("0")
Qfs = Salida biestable activado por flanco de subida
Qfb = Salida biestable activado por flanco de bajada
Nota: Las salidas Q' las ignoramos, puesto que su señal simplemente es
la inversa de Q.
Recuerda:
q
Un flip-flop activado por nivel sólo puede cambiar mientras la señal de
reloj esté en un determinado nivel: nivel alto ("1") o nivel bajo ("0").
q
Un flip-flop activado por flanco no puede cambiar de estado excepto en el
flanco de disparo de un pulso de reloj. Las entradas R y S se pueden
cambiar en cualquier momento sin que varíe la salida, salvo en esos
instantes. Para detectar los flancos, se utiliza un circuito "detector de
transición de impulsos", que se conecta a la entrada ENABLE.
Ejemplo de IC: el 74LS279 tiene 4 latches R'S'.
10
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.3 Biestable J-K
El flip-flop J-K es uno de los más ampliamente utilizados. Las
denominaciones J y K de sus entradas no tienen ningún significado conocido,
excepto el hecho de que son dos letras consecutivas del alfabeto.
Es similar al R-S, pero elimina la indeterminación que se presenta
cuando las dos entradas son "1". En este caso, para esa combinación el estado
cambia de valor, es decir, si tenía el valor "0" pasa a valor "1" y viceversa.
La razón de utilizar el biestable R-S es porque es mucho más simple y
económico que el biestable J-K. Hay muchos casos en que tenemos la certeza
de que el circuito conectado al biestable no podrá activar simultánemente las
dos entradas a la vez ("1").
La tabla de transición es la siguiente, en forma normal y forma
compacta:
J
0
0
0
0
1
1
1
1
K
0
0
1
1
0
0
1
1
Q(t) Q(t+1)
0
0
1
1
0
0
1
0
0
1
1
1
0
1
1
0
J
0
0
1
1
K
0
1
0
1
Q(t+1)
Q(t)
0
1
Q(t)'
Comentario
No cambia
Se activa Reset
Se activa Set
Invierte Q(t)
ND = No definido
El símbolo como bloque es:
J
Q
J
Clock
K
Q
Clock
Q'
Activado por flanco de subida
K
Q'
Activado por flanco de bajada
Ejemplo de IC: el 74HC112 tiene 2 flip-flops J-K (flanco de bajada), con
entradas asíncronas de inicialización y borrado.
11
Estructura de computadores
Tema 5: Sistemas secuenciales
Ejemplo de cronograma: se aplican las siguientes formas de onda a las
entradas J, K y de reloj. Determinar la salida Q para un biestable activado por
flanco de subida y para otro activado por flanco de bajada, suponiendo que se
encuentran inicialmente en estado RESET ("0").
Reloj
J
K
Qfs
Qfb
Cronograma biestables J-K (flanco de subida y flanco de bajada)
t
Donde:
Qfs = Salida biestable activado por flanco de subida
Qfb = Salida biestable activado por flanco de bajada
El biestable J-K no tiene sentido como asíncrono:
Supongamos que el estado inicial es Q(0)=0 y que J=K=1. Mirando la
tabla de transición vemos que, para las entradas indicadas, el estado cambia al
estado Q(1)=1. Ahora bien, apenas ha cambiado, como las señales de entrada
siguen indicando que cambie, volverá a cambiar a un estado Q(2)=0, y así
sucesivamente. Vemos que el funcionamiento es inestable, pues el estado
estaría cambiando continuamente.
Si por el contrario, dotamos al biestable J-K de una entrada de reloj que
sincronice las transiciones, el problema puede solucionarse. Para que
efectivamente se solucione, es necesario que la señal de reloj se active durante
un periodo de tiempo muy breve, de tal modo que en este periodo no pueda
haber más que una transición. Es conveniente pues, que la señal de reloj actúe
por flanco, reduciendo así al mínimo el período de tiempo en el cual está activa.
Para que las señales de entrada puedan ser tenidas en cuenta cuando
se producen flancos de la señal de reloj, deberán estar en unos niveles
claramente definidos. Por tanto, las restantes señales de entrada deben actuar
siempre por nivel.
12
Estructura de computadores
Tema 5: Sistemas secuenciales
Finalmente, como ya hemos comentado, hay biestables síncronos con
entradas asíncronas. El más utilizado es el J-K síncrono, con dos entradas
asíncronas adicionales, llamadas Preset (puesta a "1") y Clear (puesta a "0"),
análogas a las Set y Reset de un biestable R-S. Estas entradas PRE' y CLR'
(asíncronas) son prioritarias sobre las entradas síncronas, y se activan por nivel
bajo (las complementamos), por lo que deben mantenerse en estado alto para
el funcionamiento síncrono. El símbolo de este biestable es:
Preset ≈ Set (Biestable R-S)
PRE'
J
Q
Clock
K
Q'
CLR'
Clear ≈ Reset (Biestable R-S)
Ejemplo de cronograma para el biestable anterior, teniendo en cuenta
que Q está inicialmente a nivel bajo:
Reloj
J
K
PRE'
CLR'
Qfs
Qfb
t
Cronograma biestables J-K (síncronos y con 2 entradas asíncronas)
Debería seguir a "1" hasta el siguiente flanco
de subida pero la entrada CLR' se ha activado.
Debería cambiar a "0", pero la entrada PRE' se ha
activado; ya no podrá cambiar hasta el próximo flanco.
Donde:
PRE' = Entrada asíncrona PRESET (se ignora cuando es "1")
CLR' = Entrada asíncrona CLEAR (se ignora cuando es "1")
Qfs = Salida biestable activado por flanco de subida
Qfb = Salida biestable activado por flanco de bajada
13
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.4 Biestable D (Datos)
Sólo tiene una entrada D, y su funcionamiento es tal, que el estado
siguiente Q(t+1) es la entrada D, independientemente del estado actual del
biestable Q(t).
Su tabla de transición es:
D
0
0
1
1
Q(t) Q(t+1)
0
0
1
0
0
1
1
1
D
0
1
Q(t+1)
Comentario
0
No depende de Q(t)
1
No depende de Q(t)
Puede observarse que el nuevo estado coincide siempre con la entrada
D. Si lo definimos así, esto no es un biestable, ya que no almacena ninguna
información. Lo que ocurre es que este biestable no tiene sentido como
asíncrono.
El biestable D síncrono es un elemento típico de almacenamiento
gobernado por la señal de reloj. La señal lógica que haya en la entrada D, no
modificará el estado Q hasta que se active la señal de reloj. Esto constituye
una memoria elemental de 1 bit, ya que el valor presente en la entrada D,
queda almacenado al llegar la señal de reloj. Para cambiar el contenido de esta
celdilla de memoria, no hay más que colocar el nuevo valor en la entrada D y
activar la señal de reloj, momento en el cual el nuevo valor queda almacenado
en el biestable.
Su símbolo como bloque es:
D
Q
Clock
D
Q
Clock
Q'
Activado por flanco de subida
Q'
Activado por flanco de bajada
Puede obtenerse también a partir de un biestable J-K y un inversor,
según podemos observar en el esquema siguiente:
D
J
Q
Clock
K
Q'
J
0
0
1
1
K
0
1
0
1
Q(t+1)
Q(t)
0
1
Q(t)'
Biestable D a partir de un J-K
14
Estructura de computadores
Tema 5: Sistemas secuenciales
Ejemplo de IC: el 74AHC74 tiene 2 flip-flops D (flanco de subida), con
entradas asíncronas de inicialización y borrado.
Vamos a analizar ahora los cronogramas.
Reloj
D
Qna
Qnb
Qfs
Qfb
t
Cronograma biestables D (síncronos)
Donde:
Qna = Salida biestable activado por nivel alto ("1")
Qnb = Salida biestable activado por nivel bajo ("0")
Qfs = Salida biestable activado por flanco de subida
Qfb = Salida biestable activado por flanco de bajada
Nota: Las salidas Q' las ignoramos, puesto que su señal simplemente es
la inversa de Q.
Recuerda:
q
Un flip-flop activado por nivel sólo puede cambiar mientras la señal de
reloj esté en un determinado nivel: nivel alto ("1") o nivel bajo ("0").
q
Un flip-flop activado por flanco no puede cambiar de estado excepto en el
flanco de disparo de un pulso de reloj. Las entradas R y S se pueden
cambiar en cualquier momento sin que varíe la salida, salvo en esos
instantes.
15
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.5 Biestable T
Tiene una única entrada T. Si esta entrada está inactiva ("0"), el estado
no cambia. Si T está activa ("1"), el estado cambia.
Su tabla de transición es:
T
0
0
1
1
Q(t) Q(t+1)
0
0
1
1
0
1
1
0
T
0
1
Q(t+1)
Q(t)
Q(t)'
Comentario
No cambia el estado
Invierte el estado
Su símbolo como bloque es:
T
Q
T
Clock
Q
Clock
Q'
Activado por flanco de subida
Q'
Activado por flanco de bajada
Puede comprobarse que un biestable J-K con las dos entradas unidas
actúa como un biestable T, razón por la cual éste no existe comercialmente,
sólo existe a nivel teórico.
T
J
Q
Clock
K
Q'
J
0
0
1
1
K
0
1
0
1
Q(t+1)
Q(t)
0
1
Q(t)'
Biestable T a partir de un J-K
Por tanto, todo lo dicho para el biestable J-K es aplicable para el
biestable T.
Reloj
T
Qfs
Qfb
Cronograma biestables T (flanco de subida y bajada)
t
NOTA: Si lo hacemos por nivel (alto o bajo), el biestable estará oscilando
continuamente entre 0 y 1, cuando T=1 en el nivel correspondiente, y después
no sabremos en que estado se ha quedado.
16
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.6 Flip-flops Maestro-Esclavo
Otra clase de flip-flops son los maestro-esclavo disparados por nivel,
que han sido reemplazados progresivamente por los dispositivos disparados
por flanco.
Consiste en dos latches R-S con una entrada de habilitación (reloj), un
inversor y algún circuito adicional. Al latch de la izquierda lo llamaremos
"maestro", y al de la derecha lo llamaremos "esclavo". La diferencia es que el
"maestro" está sincronizado con una señal de reloj, y el "esclavo" lo está por
una señal de reloj invertida y se controla mediante las salidas del "maestro" en
lugar de por las entradas externas.
El "maestro" podrá cambiar de estado durante los flancos de subida, y
este estado se transfiere al "esclavo" durante el siguiente flanco de bajada. El
estado del "esclavo" depende únicamente del estado del "maestro" en el
momento que se produce el flanco de bajada, y aparece en sus salidas Q y Q'.
5.2.6.1 Biestable R-S maestro-esclavo
S
S
Reloj
Q
S
Clock
R
R
Q
Q
Q'
Q'
Clock
Q'
R
La tabla de verdad es la misma que la estudiada para biestables R-S.
J
0
0
1
1
K
0
1
0
1
Q(t+1) Comentario
Q(t)
No cambia
0
Reset
1
Set
Q(t)' Invierte Q(t)
R
0
0
1
1
S
0
1
0
1
Q(t+1)
Q(t)
1
0
ND
Comentario
No cambia
Set
Reset
No Definido
Podemos ver un ejemplo de funcionamiento en el siguiente cronograma:
Reloj
S = Sm
R = Rm
Qm = S e
Q = Qe
t
Cronograma biestable J-K Maestro-Esclavo
17
Estructura de computadores
Tema 5: Sistemas secuenciales
5.2.6.2 Biestable J-K maestro-esclavo
J
S
Q
S
Clock
Reloj
R
K
Q
Q
Q'
Q'
Clock
Q'
R
La tabla de verdad es la misma que la estudiada para biestables J-K.
J
0
0
1
1
K
0
1
0
1
Q(t+1) Comentario
Q(t)
No cambia
0
Reset
1
Set
Q(t)' Invierte Q(t)
R
0
0
1
1
S
0
1
0
1
Q(t+1)
Q(t)
1
0
ND
Comentario
No cambia
Set
Reset
No Definido
18
Estructura de computadores
Tema 5: Sistemas secuenciales
5.3 Registros y Contadores
Hasta ahora hemos estudiado circuitos combinacionales y circuitos
secuenciales por separado. En este apartado vamos a unir ambos conceptos,
para poder analizar los bloques funcionales secuenciales básicos, como son
los registros y los contadores.
Los registros y los contadores son bloques funcionales secuenciales que
se utilizan extensamente en el diseño de sistemas digitales. Los registros son
útiles para almacenar y manipular información; los contadores se emplean en
los circuitos que secuencian y controlan las operaciones de los sistemas
digitales.
5.3.1 Registros
Un registro no es más que una agrupación de biestables del mismo tipo.
Puesto que un biestable es capaz de almacenar 1 bit de información, si
tenemos "n" biestables, el registro será capaz de almacenar "n" bits de
información binaria (de forma temporal).
El registro más sencillo consta tan sólo de flip-flops sin puertas lógicas
externas. Estas puertas son las que determinan los nuevos datos a almacenar.
5.3.1.1 Registros de almacenamiento (tipo D)
El registro tipo D es un conjunto de biestables D y es el más utilizado
como almacén temporal de información. Cada entrada D se conecta a una
línea de entrada de información y cada salida Q se conecta a una línea de
salida de información. Por otro lado, todas las señales de reloj van unidas entre
sí, activando todos los flip-flops por flanco (de subida o bajada) o por nivel para
que la información se almacene en todos los biestables al mismo tiempo.
El esquema es el de la figura (para n=4 bits):
Q3
Q2
Q1
Q0
Q
Q
Q
Q
Clock
Clock
Clock
Clock
D
R
D
R
D
R
D
R
Reloj
Clear
D3
D2
D1
D0
19
Estructura de computadores
Tema 5: Sistemas secuenciales
En este caso, la señal de reloj es con flanco de subida. Además,
podemos observar como estos flip-flops tienen una entrada asíncrona de Reset
activada por 0 (Clear') para la inicialización del registro con ceros antes de su
operación, aunque esto es opcional (depende del uso que vayamos a darle al
registro en el sistema). Lo que haremos será tener la entrada Clear' a un valor
de "1" durante la operación normal sincronizada, haremos que sea "0" sólo
cuando queramos inicializar el registro.
La transferencia de información nueva a un registro se conoce como
carga del registro. Como estamos utilizando una señal de reloj por flanco
para la sincronización de todos los flip-flops, todos los bits del registro se
cargan de manera simultánea. Por ello decimos que la carga se hace en
paralelo.
La entrada de reloj en los biestables tipo D puede ser por flanco o por
nivel. La actuación por flanco requiere un circuito mucho más caro que por nivel
y no presenta ventajas salvo en casos muy particulares. Por esta razón, en los
computadores se utilizan casi siempre registros D activados por nivel, pero con
una señal de reloj, realmente se trata de actuación por nivel con señal de reloj
de corta duración.
5.3.1.2 Registros de desplazamiento
Son registros en los cuales la información contenida en un biestable
puede ser transferida al biestable adyacente. La transferencia se realiza en
todos los biestables simultáneamente, es decir, la información contenida en el
biestable 1 pasa al 2, al mismo tiempo que la información que había antes en el
2 pasa al 3, y así sucesivamente. Están conectados en cascada. La nueva
información en el primer biestable se toma de una entrada, y la información del
último biestable se pierde.
Hay varios tipos de registros de desplazamiento:
1. Atendiendo a la entrada de información en el registro:
1.1. Entrada paralelo: se puede modificar el valor de todos los biestables a
la vez (igual que en un registro tipo D).
1.2. Entrada serie: sólo hay una entrada conectada a un biestable (como
hemos descrito anteriormente).
2. Atendiendo a la salida de información:
2.1. Salida paralelo: todos los biestables son accesibles (sus salidas).
2.2. Salida serie: sólo el último biestable (su salida) es accesible. Los datos
van saliendo uno detrás de otro, mediante desplazamientos sucesivos.
3. Atendiendo al sentido del desplazamiento:
3.1. Desplazamiento sólo hacia la derecha / izquierda.
3.2. Desplazamiento en ambos sentidos, no simultáneo.
3.3. Rotación hacia la izquierda / derecha.
20
Estructura de computadores
Tema 5: Sistemas secuenciales
Para caracterizar o designar un registro de desplazamiento hay que
indicar todas sus características: tipo de entrada, tipo de salida y sentido del
desplazamiento. Por ejemplo, la designación: "SRG8" indica que es un registro
de desplazamiento (SRG, Shift Register) con una capacidad de 8 bits.
Suponiendo registros de 4 bits, los posibles movimientos de datos en
los registros de desplazamiento son:
Caso 1
Caso 2
Entrada: Serie
Salida : Serie
Desplazamiento: Hacia la derecha
Entrada: Serie
Salida : Serie
Desplazamiento: Hacia la izquierda
Entrada
Salida
Salida
Entrada
Caso 3
Caso 4
Caso 5
Entrada: Paralelo
Salida : Serie
Entrada: Serie
Salida : Paralelo
Entrada: Paralelo
Salida : Paralelo
Entradas
Entradas
Salida
Entrada
Salidas
Salidas
Caso 6
Caso 7
Desplazamiento: Rotación a la derecha
Desplazamiento: Rotación a la izquierda
Sus aplicaciones son muy numerosas. Entre ellas podemos citar:
•
•
•
•
•
•
Conversión paralelo-serie y viceversa
Rotaciones de los datos (multiplicar y dividir por 2 n )
Registros de memoria transitorios (buffers)
Sistemas para unidades aritméticas (+,·,/)
Como retardo de línea digital
Como generadores de secuencias
21
Estructura de computadores
Tema 5: Sistemas secuenciales
El circuito puede implementarse con biestables R-S, J-K o D síncronos,
con señal de reloj activa por flanco.
Veamos unos ejemplos de circuitos (esquemas).
Caso 1: Un registro de desplazamiento de 4 bits con entrada y salida
serie, desplazamiento a derecha.
Biestables R-S:
Entrada
S1 Q1
S2 Q2
S3 Q3
Clock
Clock
Clock
R1 Q1'
R2 Q2'
R3 Q3'
S4 Q4
Salida
Clock
R4
Q'
Reloj
Vamos a construir un cronograma para comprobar el funcionamiento del
registro. Suponemos que el registro se activa por flanco de subida.
Reloj
E' = R1
E = S1
Q1
Q2
Q3
S = Q4
t
Cronograma del registro con biestables R-S (síncronos con flanco de subida)
22
Estructura de computadores
Tema 5: Sistemas secuenciales
Biestables D:
Entrada
D1 Q1
Clock
Q1'
D2 Q2
Clock
Q2'
D3 Q3
Clock
Q3'
D4 Q4
Salida
Clock
Q4'
Reloj
Vamos a ver dos ejemplos de cronogramas, para comprobar el
funcionamiento, uno con flanco de subida y otro con flanco de bajada.
Reloj
E = D1
Q1
Q2
Q3
S = Q4
t
Cronograma del registro con biestables D (síncronos con flanco de subida)
Reloj
E = D1
Q1
Q2
Q3
S = Q4
t
Cronograma del registro con biestables D (síncronos con flanco de bajada)
23
Estructura de computadores
Tema 5: Sistemas secuenciales
Caso 4: Un registro de desplazamiento de 4 bits con entrada serie y
salida paralelo.
Biestables D:
Entrada
D1 Q1
D2 Q2
Clock
D3 Q3
Clock
Q1'
D4 Q4
Clock
Q2'
Clock
Q3'
Q4'
Reloj
S1
S2
S3
S4
Salidas de datos en paralelo
Caso 5: Un registro de desplazamiento de 4 bits con entrada paralelo y
salida paralelo.
Biestables D:
Entradas de datos en paralelo
E1
E2
D1 Q1
E3
D2 Q2
Clock
D3 Q3
Clock
Q1'
E4
D4 Q4
Clock
Q2'
Clock
Q3'
Q4'
Reloj
S1
S2
S3
S4
Salidas de datos en paralelo
Como podemos observar, en este tipo de registros no se realiza ningún
desplazamiento, por lo que no se puede considerar como registro de
desplazamiento.
24
Estructura de computadores
Tema 5: Sistemas secuenciales
5.3.2 Contadores
Un contador es un registro que pasa por una secuencia predeterminada
de estados al aplicársele pulsos de reloj.
Básicamente, son circuitos capaces de contar los impulsos que llegan
por una línea. El valor de la cuenta se expresa mediante un código, que en la
mayoría de los casos es binario natural, y a veces, BCD. Los impulsos de
entrada que son capaces de detectar son los flancos de la señal de entrada.
Dado que el estado del contador debe cambiar cuando llega un flanco de la
señal de entrada, se utilizan biestables T para construir los contadores,
conectando la línea con los impulsos a contar a la entrada de reloj. También
podemos utilizar biestables J-K.
5.3.2.1 Tipos de contadores
1. Atendiendo al código que cuentan
1.1. Binario (natural)
1.2. BCD
1.3. En anillo
1.4. En Gray
1.5. Johnson
2. Atendiendo al sentido de conteo
2.1. Contador hacia arriba (ascendentes)
2.2. Contador hacia abajo (descenentes)
2.3. Contador en ambos sentidos, no simultáneos
3. Atendiendo a la posibilidad de preselección
3.1. Contador con carga en paralelo
3.2. Contador con puesta a cero inicial solamente
4. Atendiendo a la forma de propagarse la señal de reloj internamente
4.1. Contador asíncrono (contadores con propagación)
4.2. Contador síncrono con acarreo serie
4.3. Contador síncrono con acarreo paralelo
Para caracterizar un contador se indican todas las posibilidades. Por
ejemplo, un contador BCD Aiken ascendente asíncrono.
Un contador es asíncrono cuando la salida del biestable es la entrada
de reloj del biestable siguiente. Estos contadores llevan una secuencia
(ascendente o descencente) que se repite indefinidamente.
Un contador es síncrono cuando la señal de reloj se conecta a la
entrada de reloj de cada uno de los biestables. Se utiliza cuando los estados
por los que pasa (secuencia) no son correlativos. Por ejemplo: 1,8,7,4, etc.
25
Estructura de computadores
Tema 5: Sistemas secuenciales
5.3.2.2 Diseño de contadores asíncronos
Supongamos un contador de módulo N, siendo (N-1) el mayor
número representable que contamos. Seguiremos los siguientes
pasos:
1. Calcular el número de biestables (flip-flops) necesarios: n.
Deberemos cumplir que:
2n-1 < N ≤ 2n
Donde: N = Número de estados (0..N-1)
n = Número de biestables (T o J-K).
2. Conectar las entradas de reloj de todos los biestables.
Activación del reloj
Flanco de bajada
Flanco de subida
Tipo contador
Ascendente
Descendente
Ascendente
Descendente
Salida a conectar a la entrada de
reloj del siguiente biestable
Q
Q'
Q'
Q
3. Conectar las entradas de todos los biestables a "1" lógico.
Biestables T:
conectando T="1"
Biestables J-K:
conectando J=K="1"
Ambos tipos podrán tener o no entradas asíncronas de PRESET Y CLEAR.
Sólo si nuestros biestables tienen una entrada asíncrona PRESET
seguimos con los siguientes pasos:
4. Escribir el número N-1 en binario.
5. Para todos los biestables que tienen un 1 en dicho valor binario, conectar su
salida Q junto con la señal de reloj en una puerta NAND.
6. Conectar la salida de la puerta NAND a las entradas PRESET del resto de
biestables, los que su valor binario era 0 en el valor N-1.
Por otro lado, sólo si nuestros biestables tienen una entrada asíncrona
CLEAR seguimos con los siguientes pasos:
4. Escribir el número N-1 en binario.
5. Para todos los biestables que tienen un 0 en dicho valor binario, conectar su
salida Q junto con la señal de reloj en una puerta NAND.
6. Conectar la salida de la puerta NAND a las entradas CLEAR del resto de
biestables, los que su valor binario era 1 en el valor N-1.
Lógicamente, si tenemos biestables con las dos entradas asíncronas
PRESET y CLEAR podemos utilizar cualquiera de los dos métodos descritos.
Si estas entradas se activan a nivel bajo lo hacemos como hemos descrito; si
se activan por nivel alto, utilizaremos una puerta AND en lugar de la NAND.
26
Estructura de computadores
Tema 5: Sistemas secuenciales
Un contador asíncrono es de módulo N cuando cuenta todos los estados
desde el 0 hasta el N-1 correlativamente.
Si nos piden diseñar un contador asíncrono módulo 5, éste contará 0,1,2,3,4.
Lo que hacemos utilizar biestables con entrada CLEAR, detectamos la última
combinación (N-1) y procedemos como hemos explicado para biestables
CLEAR, para que se reinicie la cuenta al llegar a N-1. Esto no es necesario si
fuera módulo potencia de 2, ya que se reinicia sólo. Por ejemplo, módulo 8.
Ejemplo
Vamos a ver como ejemplo, el circuito y cronograma de un contador
asíncrono de 3 bits, binario, con cuenta hacia arriba, sin preselección
(PRESET) ni puesta a cero (CLR). Utilizamos biestables T para realizar el
circuito. Recordemos la tabla de transición del biestable T:
T
0
0
1
1
Q(t) Q(t+1)
0
0
1
1
0
1
1
0
T
0
1
Q(t+1)
Q(t)
Q(t)'
Comentario
No cambia el estado
Invierte el estado
Necesitaremos "n" biestables. Tenemos que N = 8 estados. Se debe
cumplir:
2n-1 < N ≤ 2n ⇒ 2n-1 < 8 ≤ 2n ⇒ n ≥ 3
Con cuenta hacia arriba:
Q1 (LSB)
"1"
T1 Q1
Pulsos de reloj
"1"
Q2
T2 Q2
Q3 (MSB)
"1"
Clock
Clock
T3 Q3
Clock
Q2'
Q1'
Q3'
El funcionamiento se puede analizar en el siguiente cronograma:
Reloj
Q1
0
1
0
1
0
1
0
1
0
1
Q2
0
0
1
1
0
0
1
1
0
0
Q3
0
0
0
0
1
1
1
1
0
0
0
1
2
3
4
5
6
7
0
1
Cronograma reloj asíncrono 3 bits (cuenta hacia arriba)
27
t
Estructura de computadores
Tema 5: Sistemas secuenciales
Con cuenta hacia abajo:
Lo único que tenemos que cambiar en el circuito anterior es la señal de
reloj, para que se active por flanco de subida.
Q1 (LSB)
"1"
"1"
T1 Q1
Pulsos de reloj
Q2
T2 Q2
Q3 (MSB)
"1"
T3 Q3
Clock
Clock
Clock
Q2'
Q1'
Q3'
El funcionamiento se puede analizar en el siguiente cronograma:
Reloj
Q1
1
0
1
0
1
0
1
0
1
Q2
1
1
0
0
1
1
0
0
1
Q3
1
1
1
1
0
0
0
0
1
7
6
5
4
3
2
1
0
7
Cronograma reloj asíncrono 3 bits (cuenta hacia abajo)
Otra posibilidad hubiera sido conectar la salida Q' de cada biestable a la
entrada de reloj del siguiente, en vez de Q, manteniendo el flanco de bajada.
Q1 (LSB)
"1"
Pulsos de reloj
T1 Q1
Clock
Q1'
"1"
Q2
T2 Q2
Clock
Q2'
Q3 (MSB)
"1"
T3 Q3
Clock
Q3'
La mayor parte de los contadores asíncronos no funciona bien para
frecuencias elevadas, sobre todo cuando implementamos contadores con
módulo que no son potencia de 2.
Cuando utilizamos contadores que si son potencia de 2 (2,4,8,...), estos
funcionan bastante bien, tanto en modo ascendente como en modo
descendente. Sin embargo, en los otros casos conviene utilizar contadores
síncronos.
28
t
Estructura de computadores
Tema 5: Sistemas secuenciales
5.3.2.3 Diseño de contadores síncronos
Para los contadores síncronos podemos utilizar cualquier tipo de biestables:
R-S, J-K, D y T.
El procedimiento de diseño de contadores síncronos es:
1. Calcular el número de biestables (flip-flops) necesarios: n.
Deberemos cumplir que:
Donde:
2n-1 < N ≤ 2n
N = Número de estados
n = Número de biestables (R-S, J-K, D ó T).
2. Escribimos la tabla de funcionamiento del biestable .
3. Construimos una tabla de transiciones y excitaciones correspondientes
a las entradas del biestable utilizado. En esta tabla, averiguamos el valor
que deben de tener las entradas del biestable para que en la salida se
produzca cualquier transición (0-0, 0-1, 1-0, 1-1).
4. Utilizando esta última tabla, construimos la tabla de transiciones y
excitaciones del contador. En esta tabla averiguamos el valor que
debemos tener en las entradas para producir la secuencia de estados
pedida. Lo que conocemos son las salidas Q de los biestables, puesto que
son las combinaciones que queremos que cuente. Por tanto, ponemos
como posibles combinaciones de entrada los distintos valores que va a
contar en binario, y se trata de calcular las funciones lógicas
correspondientes a cada una de las entradas de los biestables en función
de las salidas.
5. Simplificar por Karnaugh las funciones lógicas obtenidas. Las tablas de
Karnaugh se pueden obtener directamente de la tabla anterior.
6. Realización del circuito a partir de las funciones simplificadas.
7. Comprobar el funcionamiento realizando un cronograma.
29
Estructura de computadores
Tema 5: Sistemas secuenciales
Ejemplo
Vamos a diseñar un contador que siga la siguiente secuencia con
biestables J-K: 0, 4, 6, 1, 14, 7 y vuelvan a repetirse. Utilizamos biestables J-K,
sin preselección (PRESET) ni puesta a cero (CLR).
1. Número de biestables:
Tenemos 6 posibles estados (N=6), por tanto:
2n-1 < N ≤ 2n
⇒ 2n-1 < 16 ≤ 2n
En este ejemplo vamos a utilizar n=4.
⇒ n≥ 3
2. Tabla de funcionamiento del biestable:
J
0
0
1
1
K
0
1
0
1
Q(t+1)
Q(t)
0
1
Q(t)'
Comentario
No cambia
Reset
Set
Invierte Q(t)
3. Tabla de transiciones y excitaciones de las entradas del biestable:
Transición
Q(t) ⇒ Q(t+1)
0⇒0
0⇒1
1⇒0
1⇒1
J
K
0
1
X
X
X
X
1
0
¿Qué valores pueden tomar las
entradas J-K para conseguir
dicha transición en la salida?
4. Tabla de transiciones y excitaciones del contador:
Q1
0
0
0
0
1
0
Q2
0
1
1
0
1
1
Q3
0
0
1
0
1
1
Q4
0
0
0
1
0
1
J1
0
0
0
1
X
0
K1
X
X
X
X
1
X
J2
1
X
X
1
X
X
K2
X
0
1
X
0
1
J3
0
1
X
1
X
X
K3
X
X
1
X
0
1
J4
0
0
1
X
1
X
K4
X
X
X
1
X
1
Para cada biestable x, rellenamos las columnas de Jx y Kx con los
valores que deben tomar las entradas para que en el siguiente estado cambie
su correspondiente Qx al valor del siguiente valor de la secuencia; si fuese el
último, entonces consideramos de nuevo el primero para que comience de
nuevo el ciclo.
30
Estructura de computadores
Tema 5: Sistemas secuenciales
5. Simplificamos por Karnaugh las funciones de las entradas.
q
J1 = Q2'
Q3 Q4
Q1Q2
00
00
01
11
10
0
1
X
X
0
X
0
0
X
X
X
X
X
X
X
X
01
11
10
q
q
K1 = 1
Q3 Q4
Q1Q2
00
K2 = Q1'
Q3 Q4
Q1Q2
00
01
01
11
10
01
11
10
01
X
X
X
X
X
X
1
1
X
X
X
0
X
X
X
X
0
1
X
X
1
X
X
X
X
X
X
X
X
X
X
X
00
01
11
10
X
X
X
X
X
X
1
1
X
X
X
0
X
X
X
X
J4 = Q3
Q3 Q4
Q1Q2
00
00
10
K3 = Q1'
Q3 Q4
Q1Q2
00
q
q
11
10
10
J2 = 1
01
11
11
q
00
01
q
No es necesario construir un
mapa de Karnaugh pues todas
las casillas serán X menos un
"1". Como podremos hacer un
grupo de 16 casillas (todas), la
función lógica será "1".
J3 = Q2+Q4
11
10
q
00
01
11
10
0
X
X
X
0
X
X
1
X
X
X
1
X
X
X
X
K4 = 1
31
Estructura de computadores
Tema 5: Sistemas secuenciales
6. Circuito a partir de las funciones simplificadas.
Q1 (MSB)
J1
Q1
J2
CLK1
K1
Q2
Q2
Q3
J3
CLK2
Q1'
K2
Q4 (LSB)
Q3
J4
CLK3
Q2'
K3
Q4
CLK3
Q3'
K4
Q4'
Reloj
"1"
7. Cronograma:
Reloj
0
0
0
0
1
0
0
0
0
1
0
1
1
0
1
1
0
1
1
0
0
0
1
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
0
1
0
4
6
1
14
7
0
4
6
1
(MSB) Q1
Q2
Q3
(LSB) Q4
Cronograma reloj síncrono (Secuencia: 0, 4, 6, 1, 14, 7)
NOTA: Para construir el cronograma, como ahora cambian todos los
biestables al mismo tiempo, tendremos que mirar la entrada de cada uno en el
estado anterior.
Ejemplos de IC:
q
q
q
q
74LS93: Asíncrono binario 4 bits
74LS163: Síncrono binario de 4 bits
74LS160: Décadas BCD síncrono
74LS190: Décadas ascendente / descendente
32
t