Circuito equivalente de un motor de inducción
Anuncio
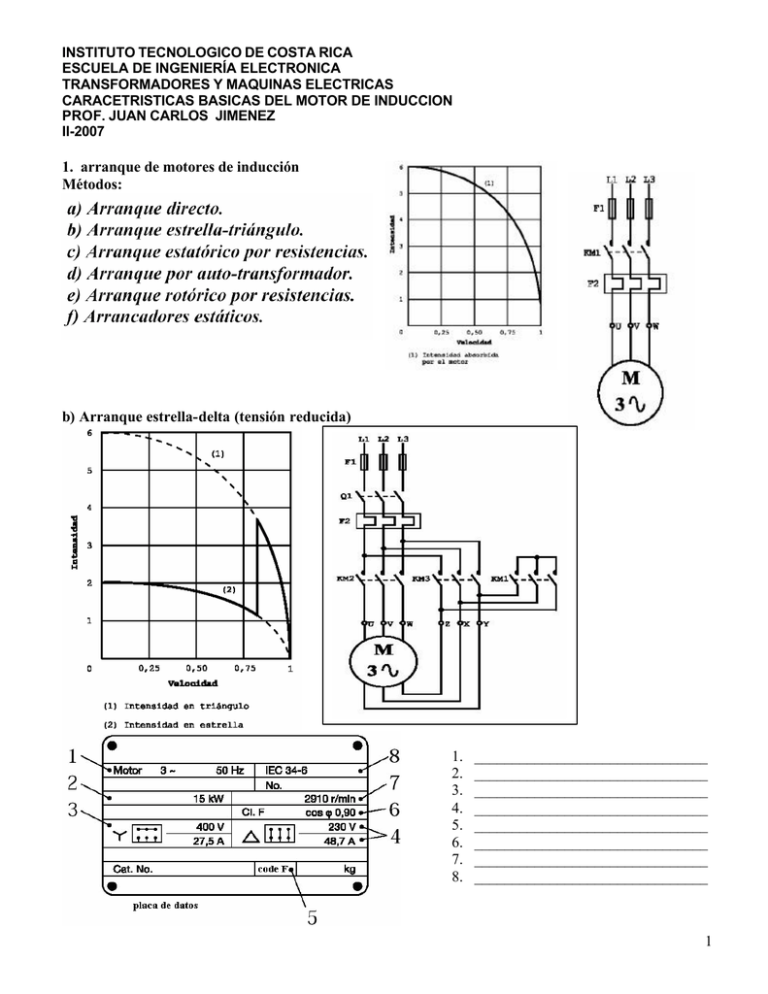
INSTITUTO TECNOLOGICO DE COSTA RICA ESCUELA DE INGENIERÍA ELECTRONICA TRANSFORMADORES Y MAQUINAS ELECTRICAS CARACETRISTICAS BASICAS DEL MOTOR DE INDUCCION PROF. JUAN CARLOS JIMENEZ II-2007 1. arranque de motores de inducción Métodos: b) Arranque estrella-delta (tensión reducida) 1. 2. 3. 4. 5. 6. 7. 8. _______________________________ _______________________________ _______________________________ _______________________________ _______________________________ _______________________________ _______________________________ _______________________________ 1 c) Arranque estatórico por resistencias d) arranque por autotransforma dor e) arranque rotórico por resistencias f) arrancadores estáticos Se utilizan circuitos electrónicos de potencia mediante tiristores para el arranque. 2 Resumen: La corriente de arranque puede elevarse hasta un valor muy superior sobre la corriente nominal y se corre el riesgo de dañar el motor, las líneas de alimentación y las protecciones. En la placa de datos se especifica una letra código con la que es posible calcular la corriente de arranque del motor. Según las compañías eléctricas, se exige un sistema de arranque para el motor a partir de cierta potencia y en Costa Rica para potencias superiores a 30HP, se hace necesario un mecanismo de arranque. Para el calcular la corriente se emplea la siguiente tabla: IA = HP * factor _ código 3 *VL calcule I A si el motor es de 240V, 36 A, 15HP, y letra E 2. Control de velocidad de motores de inducción a. variar el deslizamiento. Existen dos mecanismos para variar el deslizamiento, uno es por variación de la tensión de alimentación a través del control del ángulo de disparo de tiristores pero el rango de variación es limitado. El segundo solo es aplicable a motores de inducción de anillos rozantes y consiste en agregar resistencias retóricas variables. Este método reduce grandemente la eficiencia de la máquina a la vez que es muy simple. Control de velocidad mediante variación de la tensión Control por medio de resistencias estatóricas 3 b. variar la velocidad sincrónica. Esto se consigue variando la frecuencia de la tensión de alimentación a través de sistemas electrónicos llamados “variadores de frecuencia” con los cuales es posible ajustar la velocidad por encima o por debajo de la velocidad nominal. Recordar que ns = 120 f p c. cambiar el número de polos P. Se aplica en motores que posee bobinados múltiples de modo que con conexiones externas sea posible cambiar el número de polos. La variación por tanto es discreta es decir solo se pueden obtener variaciones fijas de 1800, 1200, 900, 600 rpm. 3. Circuito equivalente de un motor de inducción Un motor de inducción depende para su funcionamiento de que el circuito del estator induzca voltajes y corrientes en el circuito del rotor (acción transformadora). Puesto que la inducción de voltajes y corrientes en el circuito del rotor de un motor de inducción es, esencialmente, una acción de transformación, el circuito equivalente de un motor eléctrico de inducción terminará por ser muy similar al circuito equivalente de un transformador. Como en cualquier transformador, hay una cierta resistencia y auto inductancia en los embobinados primarios (estator), los cuales se representan en el circuito equivalente de la máquina. La resistencia del estator se denominará R1 y la reactancia de dispersión del estator X1. Ambos componentes aparecen justo a la entrada del modelo de la máquina. También, como en cualquier transformador con un núcleo de hierro, el flujo de la máquina está relacionado con el voltaje aplicado E1. La existencia de un entrehierro del motor de inducción, que aumenta enormemente la reluctancia de la trayectoria del flujo y por tanto debilita el acoplamiento entre el primario y el secundario. A mayor reluctancia causada por el entrehierro, mayor corriente de magnetización se necesita para lograr un nivel de flujo determinado. Por lo tanto, la reactancia de magnetización en el circuito equivalente XM tendrá un valor menor que el correspondiente a un transformador. Para modelar las pérdidas en el núcleo es necesaria además la resistencia Rc . El voltaje interno del estator E1 se acopla con el secundario ER por medio de un transformador ideal de relación de espiras a ef . Aunque en el caso de los motores de jaula de ardilla es difícil definir esta relación, existe una relación de espiras efectiva para el motor. En un motor de inducción, cuando se aplica el voltaje a los embobinados del estator, se induce un voltaje en los embobinados del rotor. En general, cuanto mayor sea el movimiento relativo entre los campos magnéticos del rotor y el estator, mayor será el voltaje resultante en el rotor. El mayor movimiento relativo se da cuando el rotor se haya en estado estacionario, condición conocida como de rotor frenado o rotor bloqueado. El extremo opuesto (0V) se da cuando no hay movimiento relativo. El voltaje inducido en cualquier caso entre los dos extremos es directamente proporcional al deslizamiento. Siendo ER 0 el voltaje inducido con rotor bloqueado, entonces E R = s * ER 0 La reactancia del rotor de un motor de inducción depende de la inductancia LR, de la frecuencia del voltaje fe y de la corriente del rotor. Por lo que X R = 2π * s * f e * LR =s* X R0 , donde X R0 es la reactancia del rotor con este bloqueado y f e la frecuencia de la red. La resistencia del rotor se denomina RR. Fig. 1 Circuito equivalente inicial de un motor de inducción. 4 La corriente en el secundario (rotor) queda entonces como Si se divide por el deslizamiento: I R = s * ER 0 /( RR + s * jX R 0 ) I R = E R0 /( RR / s + jX R 0 ) Es posible tratar los efectos del rotor, debido a su velocidad variable, como causados por una impedancia variable alimentada por una fuente de potencia de voltaje constante ER0. De esta forma queda la siguiente impedancia: Z R = ( RR / s + jX R 0 ) Finalmente se traslada los voltajes, corrientes e impedancias del secundario al primario por medio de la relación de espiras del transformador. E1 = aef * ER 0 I 2 = I R / a ef Z 2 = ( aef ) 2 * ( RR / s + jX R0 ) Si ahora se hacen las siguientes definiciones R2 = ( aef ) 2 * RR X 2 = ( aef ) 2 * X R0 el circuito equivalente queda como en la Fig.2 Fig. 2 Circuito equivalente final de un motor de inducción. La resistencia del rotor RR, la reactancia del rotor bloqueado XR0 y la relación de espiras a ef son difíciles o imposibles de determinar en los rotores de jaula de ardilla. Sin embargo, es posible tomar medidas que dan directamente los valores de R2 y X2. 5 4. Pérdidas en un motor de inducción Fig. 3 estimación de pérdidas en el motor de inducción Fig. 4 tipos de pérdidas en el motor de inducción 5. Análisis del circuito equivalente I 1 = Vφ / Z eq Pérdidas en el estator: Pcu = 3I R1 2 1 y PNU 3V 2 = RC PROT = 3I 22 R2 también PROT = sPAG R PAG = Pi − Pcu − PNU además PAG = 3I 22 2 s 1− s Pconv = PAG − Prot y ahora Pconv = 3I 22 R2 ( ) Finalmente Pconv = PAG (1 − s ) s Potencia de salida (mecánica) Po, P0 = Pconv − Pfricc − Potras Pérdidas en el rotor: Torque inducido por la máquina (interno) τ ind = Pconv PAG = ωm ωs donde ω m es la velocidad del motor y ω s es la velocidad sincrónica del campo giratorio Torque de carga τC = P0 ωm 6 ANALISIS DE LA CURVA DE TORQUE INDUCIDO Para obtener una expresión matemática del torque inducido es necesario primeramente encontrar una relación de la corriente I 2 en función de la tensión de thevenin. El equivalente se obtiene entre los puntos a y b indicados. Para facilitar los cálculos se tienen varias suposiciones, por ejemplo que Rc = ∞ VTH = Vφ + jX m la magnitud de este número complejo es: R1 + j ( X 1 + X m ) VTH = si consideramos que X m >> R1 , entonces R1 se puede despreciar y VTH = Z TH = Vφ * X m R + ( X1 + X m ) 2 2 1 Vφ * X m X m + X1 jX m ( R1 + jX 1 ) , ahora si se asume que X m >> X 1 y que X m + X 1 >> R1 entonces la parte real R1 + j ( X 1 + X m ) de este número complejo es RTH y RTH ≈ R1 ( Xm ) 2 , de la misma forma la parte imaginaria es X TH , X1 + X m por tanto X TH ≈ X 1 . El circuito equivalente de thevenin queda entonces: I2 = VTH = Z TH + Z 2 (RTH + 3 VTH R2 + j ( X TH + X 2 ) s 2 R2 2 ) + ( X TH + X 2 ) 2 s R2 s PAG 2 R2 = y que PAG = 3 I 2 por tanto R2 2 ωS s 2 (RTH + s ) + ( X TH + X 2 ) 2 R2 3 VTH s (1) R2 2 2 + ) + ( X TH + X 2 ) s Recuerde que τ ind = ω S (RTH RTH + VTH I2 = τ ind = VTH Si s=1, n=0, esto es en el arranque por lo que 2 τ ARR = [ 3 VTH R2 ωS (RTH + R 2 ) 2 + ( X TH + X 2 ) 2 ] La potencia máxima coincide con τ max . Si se toma la máxima transferencia de potencia, se debe cumplir que R2 sea igual a la magnitud de la impedancia de la fuente, es decir Z s = RTH + j ( X TH + X 2 ) por eso s 7 R2 2 = RTH + ( X TH + X 2 ) 2 existe máxima transferencia y se puede despejar el s R2 deslizamiento al cual el torque es máximo: s MAX = sustituyendo en (1) se tiene: 2 RTH + ( X TH + X 2 ) 2 si se cum ple que τ MAX = [ 3 VTH 2 2 2ω S RTH + RTH + ( X TH + X 2 ) 2 ] Ejercicio 1: Un motor de anillos rozantes de 460V, 25HP, 60Hz, 4 polos conectado en Υ , tiene los mismos valores de los parámetros del circuito equivalente del problema visto en clase. 1. 2. 3. 4. 5. calcular el valor del torque máximo, a que velocidad se da y cual es el deslizamiento cual es el valor del torque de arranque si se duplica el valor de la resistencia del rotor R2 , calcule nuevamente el torque máximo calcule para la condición anterior, el torque de arranque, analice el resultado obtenido, justifique. calcule el valor de R2 para que el motor arranque con el máximo torque posible, es decir cuando τ ARR = τ MAX 6. si la carga tiene un comportamiento par-velocidad descrito por la siguiente expresión τ c = 60 e9.229 x10 −3 ωm Nm, primero analice si el accionamiento puede arrancar y luego calcule en forma aproximada la velocidad final del accionamiento. Ejercicio 2: calcule lo mismo que en el ejemplo anterior con el siguiente motor: 5 HP, 4 POLOS, 220 V, 3φ, 60 HZ, Inom=12.9 A, conexión Υ . Las pérdidas por rotación de 176W a un deslizamiento del 3%. Nota: El motor de anillos rozantes es una variedad de motor de inducción que funciona de la misma forma que el jaula de ardilla, con la diferencia en la estructura del rotor. En este tipo, el rotor es bobinado con cobre, normalmente tres bobinas conectadas en estrella internamente y llevadas al exterior a la caja de bornes mediante tres anillos de cobre montados en el eje del rotor. Estos anillos rozan con sendas escobillas y queda a criterio del usuario que hacer con estas tres terminales. Si se conectan tres resistencias variables, es posible no solo limitar la corriente de arranque sino también poder variar la velocidad en cierto rango. 8




