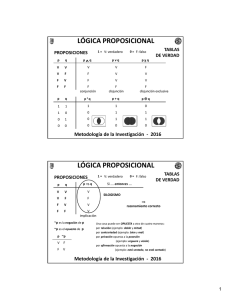
Cálculo Proposicional

Universidad Técnica Federico Santa María
Departamento de Informática
Fundamentos de Informática 1
Cálculo Proposicional
Dr. Gonzalo Hernández Oliva
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
1
Cálculo Proposicional:
1)
2)
3)
4)
5)
6)
Motivación
Introducción
Argumentos y Proposiciones Lógicas
Conectivos Lógicos
Estudio Proposiciones
Tautología, Contradicción y Argumento
Válido
7) Leyes Álgebra Proposicional
8) Formas Normales
9) Implicaciones y Derivaciones Lógicas
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
2
Cálculo Proposicional:
1) Motivación:
Problema NP: Problema SAT
Enumerar (Hacer una lista) todos los
valores de verdad de una proposición
lógica.
Algoritmo Backtracking
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
3
Cálculo Proposicional:
2) Introducción
ƒ La Lógica resulta esencial para construir,
diseñar, implementar y probar correctitud en
algoritmos y programas.
ƒ Es necesario estudiar las Leyes
Fundamentales de las Derivaciones Lógicas
para estudiar la validez de las afirmaciones
realizadas
ƒ Las Proposiciones forman las Derivaciones y
sus Operaciones el Cálculo Proposicional
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
4
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
ƒ Argumentos (Afirmaciones, Conclusiones,
Demostraciones) son Válidos o No
Lógicamente: V ó F
ƒ Proposiciones forman los Argumentos
ƒ Proposiciones Atómicas son aquellas
proposiciones que no pueden subdividirse y
pueden unirse por conexiones lógicas
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
5
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
Ejemplos:
1) P: Si la demanda crece entonces las
compañias se expanden.
P: Si las compañias se expanden
entonces contratan trabajadores.
C: Si la demanda crece entonces las
compañías contratan trabajadores.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
6
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
2) Este programa de computadora tiene un
error, o el input es erróneo. El input no es
erróneo. El programa de computadora
tiene un error.
3) Una universidad es de prestigio si los
académicos que la forman realizan
docencia e investigación de gran calidad.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
7
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
4) La extracción de mineral es rentable si la
concentración es alta, pero solamente si
la distancia al mercado es pequeña.
5) Si llueve con frecuencia los agricultores
se quejan. Si no llueve con frecuencia los
agricultores se quejan. Luego, los
agricultores se quejan.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
8
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
De manera formal: (Aristóteles)
ƒ Una proposición es una afirmación que
es o bien verdadera o bien falsa.
ƒ Elementos de una proposición:
9 Variables Proposicionales: Asignación
de Valor Lógico Binario: V ó F
9 Constantes Proposicionales: V , F
9 Conectivos u Operaciones Lógicas
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
9
Cálculo Proposicional:
3) Argumentos y Props. Lógicas
Proposición Atómica:
ƒ Una proposición atómica es una
proposición que tiene una única variable o
constante proposicional.
ƒ Las proposiciones no atómicas se
denominan compuestas.
ƒ Todas las proposiciones compuestas
tienen al menos una conexión lógica
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
10
Cálculo Proposicional:
4) Conectivos Lógicos
ƒ Los conectivos lógicos son operadores entre
props. que permiten construir proposiciones
complejas en base a proposiciones más
simples o atómicas. Los conectivos lógicos
básicos son:
Negación:
∼P
Conjunción:
P∧Q
Disyunción:
P∨Q
Condicional:
P⇒Q
Bicondicional o Equivalencia: P ⇔ Q
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
11
Cálculo Proposicional:
4) Conectivos Lógicos
ƒ Los conectivos lógicos se definen mediante su
tabla de verdad:
P Q ∼P ∼Q P∨Q P∧Q P⇒Q P⇔Q
V
V
F
F
V
F
V
F
F
F
V
V
F
V
F
V
V
V
V
F
V
F
F
F
V
F
V
V
V
F
F
V
ƒ Para su operación se ha definido un orden en
base a su prioridad:
Alta (∼) → (∧) → (∨) → (⇒) → (⇔) Baja
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
12
Cálculo Proposicional:
5) Estudio Proposiciones
ƒ Para estudiar proposiciones lógicas o
expresiones más complejas se tienen 2
herramientas fundamentales:
Î Tablas
de Verdad: Obtenido en base a las
expresiones más simples y proposiciones
atómicas que las forman
Î Árbol de Análisis Sintáctico:
Descomposición de la expresión en base
a sus proposiciones atómicas.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
13
Cálculo Proposicional:
5) Estudio Proposiciones: TV
ƒ Dada una proposición es posible estudiar su
validez asignando valores de verdad a sus
proposiciones atómicas y calcular los
valores de verdad de las proposiciones
compuestas que la forman en base a las
definiciones de los conectivos lógicos.
Todas las posibilidades de este cálculo
lógico se resumen en una Tabla de Verdad
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
14
Cálculo Proposicional:
5) Estudio Proposiciones TV
Ejemplos:
1) P ⇒ (Q ∧ R) ∧ (∼ P ⇒ R)
2) (P ∨ R) ∧ ∼ (P ∨ Q) ⇒ Q ∨ R
3) (P ∨ (Q ⇒(R ∧ ∼P ))) ⇔ (Q ∧ R)
4) (P ∧ Q) ∨ (∼P ∧ Q ) ∨ (P ∧ ∼Q )∨ ∼Q
5) Si Micaela gana en las Olimpiadas, todos la
admirarán y ella será muy feliz, pero si no
gana, todo su esfuerzo fue en vano
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
15
Cálculo Proposicional:
5) Estudio Proposiciones
6) La extracción de minerales es provechosa
si la concentración de mineral es alta pero
sólo si la distancia al mercado es corta
7) Si p es un número primo entonces para
los enteros pares (np–n) es divisible por p
8) Los productos comprados en esta tienda
pueden ser devueltos sólo si están en
buenas condiciones y el cliente trae la
boleta
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
16
Cálculo Proposicional:
6) Tautología y Contradicción
ƒ Una Expresión Lógica es una Tautología si
es Verdadera para todas las asignaciones
posibles de valores de verdad. En este caso
se antepondrá el símbolo |=
ƒ Una Expresión Lógica es una Contradicción
si es Falsa para todas las asignaciones
posibles de valores de verdad.
ƒ Una Expresión Lógica que no es una
tautología ni una contradicción es una
Contingencia (Causalidad/Eventualidad).
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
17
Cálculo Proposicional:
6) Tautologías
ƒ Ejemplo tautología: Ley del Medio Excluido:
|= P ∨ ∼P
ƒ Teorema: Sea A una expresión tautológica y
sean P1 ... Pn sus variables proposicionales.
Suponga que B1 ... Bn son expresiones
arbitrarias. La expresión obtenida al
reemplazar Pi por Bi es una esquema y toda
particularización (ejemplo) de este esquema
es una tautología.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
18
Cálculo Proposicional:
6) Tautologías
Tipos de Tautologías:
ƒ Implicaciones Lógicas: |= A ⇒ B (A ≡ > B)
ƒ Equivalencias Lógicas: |= A ⇔ B (A ≡ B)
Este tipo de tautología se utiliza para
demostrar y construir nuevas leyes (Álgebra
de Proposiciones)
Cabe hacer notar que: A ⇔ B ≠ A ≡ B
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
19
Cálculo Proposicional:
6) Argumento Válido
ƒ Diremos que un argumento lógico es válido si
la conclusión se deduce lógicamente de las
premisas: Si todas las premisas son
verdaderas entonces también lo es la
conclusión.
ƒ Luego, si A es la conjunción de todas las
premisas y C la conclusión, entonces:
|= A ⇒ C . Ejemplo: Silogismo Disjuntivo:
|= (P ∨ Q) ∧ ∼P ⇒ Q
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
20
Cálculo Proposicional:
7) Leyes Álgebra Proposicional
1) Medio Excluido: (P ∨ ∼ P) ≡ V
2) Contradicción: ( P ∧ ∼ P) ≡ F
3) Identidad:
4) Dominación:
(P ∨ F) ≡ P , (P ∧ V) ≡ P
(P ∨ V) ≡ V , (P ∧ F) ≡ F
5) Idempotencia: (P ∨ P) ≡ P , (P ∧ P) ≡ P
6) Doble Negación: ∼ (∼ P ) ≡ P
7) Absorción:
Dr. Gonzalo Hernández
P ∧ (P ∨ Q) ≡ P
P ∨ (P ∧ Q) ≡ P
USM FI-1 Cálculo Proposicional
21
Cálculo Proposicional:
7) Leyes Álgebra Proposicional
8) Conmutatividad : P ∨ Q ≡ Q ∨ P
P∧Q≡ Q∧P
9) Asociatividad:
(P ∨ Q) ∨ R ≡ P ∨ (Q ∨ R)
(P ∧ Q) ∧ R ≡ P ∧ (Q ∧ R)
10) Distributividad:
P ∨ (Q ∧ R) ≡ (P ∨ Q ) ∧ (P ∨ R )
P ∧ (Q ∨ R) ≡ (P ∧ Q )∨ (P ∧ R )
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
22
Cálculo Proposicional:
7) Leyes Álgebra Proposicional
11) Leyes de DeMorgan:
∼ ( P ∨ Q ) ≡ (∼ P ∧ ∼ Q )
∼ ( P ∧ Q ) ≡ (∼ P ∨ ∼ Q )
12) Implica:
P ⇒ Q ≡ (∼ P ∨ Q )
13) Contrarecíproca:
P ⇒ Q ≡ (∼ Q ⇒ ∼ P)
14) Equivalencia:
P ⇔ Q ≡ (∼ P ∨ Q ) ∧ ( P ∨ ∼ Q )
P⇔Q≡ (P⇒Q)∧ (Q⇒P)
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
23
Cálculo Proposicional:
7) Leyes Algebra Proposicional
Ejercicios:
ƒ Expresar las siguientes proposiciones en
base a los conectivos: ∨ ∧ ∼
1) P ⇒ Q ∨ ∼ (P ⇒ Q)
2) P ⇔ (Q ∧ P) ⇒ Q
3) P ∧ (P ⇒ Q) ⇒ Q
4) P ⇒ (Q ∧ R) ⇒ ∼ (P ⇒ F)
5) ∼ (P ⇒ Q) ∧ ( P ⇔ R ) ∨ ( Q ⇒ V )
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
24
Cálculo Proposicional:
8) Formas Normales
ƒ Una Expresión Lógica está en forma
normal disyuntiva si está escrita como
una disyunción de términos que son
conjunciones de variables lógicas o de
negaciones de variables lógicas.
ƒ Análogamente se define forma normal
conjuntiva.
ƒ Ejemplos:
P ∨ (∼ Q ∧ R ) , (P ∨ Q ∨ R) ∧ (∼ Q ∨ R) ∧ R
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
25
Cálculo Proposicional:
8) Formas Normales
ƒ Pasos para obtener la forma normal
conjuntiva (disyuntiva) de una proposición
lógica PL mediante la aplicación de las
leyes del álgebra proposicional:
1o) Eliminar en PL todos los conectivos ⇔ y ⇒
2o) Eliminar subexpresiones de PL que están
negadas. Por ejemplo: ∼ (P ∨ R)
3o) Aplicar las leyes de distributividad
4o) Ordenar la expresión
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
26
Cálculo Proposicional:
8) Formas Normales
ƒ Ejercicio: Obtener la forma normal
conjuntiva (disyuntiva) de:
a) (P∨ Q) ∧ (P ∧ (Q ∨ R)) ∨ ∼ ( P ∨ (R∧ Q ))
b) (P ⇒ Q) ∧ ∼((P ⇔ R) ∨ ∼(R ∧ Q))
ƒ Podemos construir una forma normal
disyuntiva a partir de la tabla de verdad de
una expresión lógica.
ƒ Aprendamos cómo mediante un ejemplo …
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
27
Cálculo Proposicional:
8) Formas Normales
P
V
V
V
V
F
F
F
F
Q
V
V
F
F
V
V
F
F
Dr. Gonzalo Hernández
R
V
F
V
F
V
F
V
F
PL
V
V
V
F
V
F
F
F
Obtenemos la proposición
lógica PL(P,Q,R) en forma
normal disyuntiva partir de
su tabla de verdad:
PL(P,Q,R) = …
USM FI-1 Cálculo Proposicional
28
Cálculo Proposicional:
8) Formas Normales
ƒ Un término mínimo (minterm) es una
conjunción de literales en los cuales cada
variable o su negación se representa una
única vez y cada término será verdadero
para sólo una asignación de valores de
verdad.
ƒ Si una expresión lógica esta expresada
como una disyunción de términos mínimos
se denomina forma normal disjuntiva
completa
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
29
Cálculo Proposicional:
8) Formas Normales
ƒ Pasos para obtener la forma normal
conjuntiva de una proposición lógica PL
mediante su tabla de verdad de:
1o) Obtener formal normal disyuntiva de ∼PL
2o) Negar formal normal disyuntiva de ∼PL
aplicando leyes del álgebra proposicional
ƒ Veamos un ejemplo …
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
30
Cálculo Proposicional:
8) Formas Normales
P
V
V
V
V
F
F
F
F
Q
V
V
F
F
V
V
F
F
Dr. Gonzalo Hernández
R
V
F
V
F
V
F
V
F
PL
V
V
V
F
V
F
F
V
Obtenemos la proposición
lógica PL(P,Q,R) en forma
normal conjuntiva partir de
su tabla de verdad:
PL(P,Q,R) = …
USM FI-1 Cálculo Proposicional
31
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Diremos que un argumento lógico es válido
si la conclusión se deduce lógicamente de
las premisas.
ƒ Si A es la conjunción de todas las premisas
y C la conclusión, entonces: |= A ⇒ C
ƒ A continuación veremos herramientas =
Implicancias Lógicas para demostrar si un
argumento es válido – Razonamiento
Válido.
ƒ Un argumento no válido es una falacia
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
32
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Un ejemplo de razonamiento válido es el:
P≡V
P⇒ Q ≡ V Modus Ponens
Q≡V
ƒ Esta conclusión se denota: P , P⇒ Q |= Q
ƒ Otro ejemplo:
(P ∨ Q) ≡ V
Silogismo Disjuntivo
∼P ≡ V
|= (P ∨ Q) ∧ ∼P ⇒ Q
Q≡V
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
33
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
Reglas de Inferencia:
1) Leyes de Combinación: A , B |= A
2) L. de Simplificación: A ∧ B |= A
A ∧ B |= B
A |= A ∨ B
B |= A ∨ B
3) Leyes de Adición:
4) Modus Ponens:
A , A ⇒ B |= B
5) Modus Tollens:
∼ B , A ⇒ B |= ∼ A
6) Silog. Hipotético:
Dr. Gonzalo Hernández
A ⇒ B , B⇒ C |= A⇒ C
USM FI-1 Cálculo Proposicional
34
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
Reglas de Inferencia:
7) Silog. Disyuntivo: A∨ B ,∼ A |= B
A∨ B ,∼ B |= A
8) Ley de Casos:
A ⇒ B , ∼ A ⇒ B |= B
9) Eliminación de Equivalencias:
A ⇔ B |= A ⇒ B
A ⇔ B |= B ⇒ A
10) Introducción de la Equivalencia:
A ⇒ B , B ⇒ A |= A ⇔ B
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
35
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
Reglas de Inferencia:
11) Ley de Inconsistencia: A , ∼ A |= B
ƒ Estas reglas de inferencia se utilizan para
realizar derivaciones o demostraciones
formales.
ƒ Veamos un ejemplo de derivación lógica
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
36
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ “Y ahora llegamos a la gran pregunta del
porqué. El robo no ha sido el objeto del
asesinato, puesto que nada desapareció.
¿ Fue por motivos políticos, o fue una mujer ?
Esta es la pregunta con que me enfrento.
Desde el principio me he inclinado hacia esta
última suposición …
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
37
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Los asesinos políticos se complacen
demasiado en hacer sólo su trabajo y huir.
Este asesinato, por el contrario ha sido
realizado muy deliberadamente, y quien lo
perpetró ha dejado huellas por toda la
habitación, mostrando que estuvo ahí todo el
tiempo”
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
38
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Análisis de la derivación lógica:
P1 : Fue un robo
P2 : Algo desapareció
P3 : Fue un asesinato político
P4 : El asesinato lo cometió una mujer
P5 : El asesino huyó inmediatamente
P6 : El asesino dejó huellas por la habitación
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
39
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Derivación lógica:
1)
2)
3)
4)
5)
6)
7)
P1 ⇒ P2
∼ P2
∼ P1
∼ P1 ⇒ P3 ∨ P4
P3 ∨ P4
P3 ⇒ P5
P6 ⇒ ∼ P5
Dr. Gonzalo Hernández
(Premisa)
(Premisa)
(1 y 2 + MT)
(Premisa)
(3 y 4 + MP)
(Premisa)
(Premisa)
USM FI-1 Cálculo Proposicional
40
Cálculo Proposicional:
9) Implicaciones y Deriv. Lógicas
ƒ Derivación lógica:
8) P6
9) ∼ P5
10) ∼ P3
11) Ergo : P4
Dr. Gonzalo Hernández
(Premisa)
(7 y 8 + MP)
(6 y 9 + MT)
(5 y 10 + MT)
USM FI-1 Cálculo Proposicional
41
Cálculo Proposicional:
10) Bibliografía
1) Matemáticas Discreta y Lógica, W. K.
Grassmann & J. P. Tremblay, Prentice Hall,
1998.
2) R.P. Grimaldi, Discrete and Combinatorial
Mathematics, Addison Wesley,1998.
Dr. Gonzalo Hernández
USM FI-1 Cálculo Proposicional
42