Ejercicios de Análisis de Circuitos

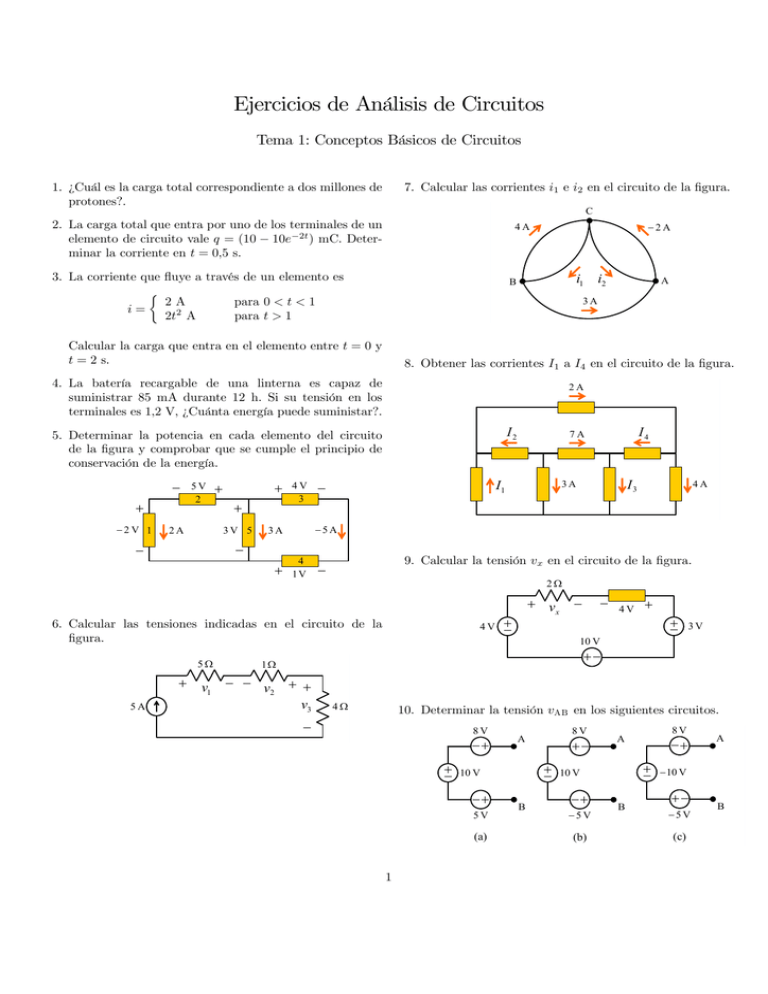
Ejercicios de Análisis de Circuitos
Tema 1: Conceptos Básicos de Circuitos
1. ¿Cuál es la carga total correspondiente a dos millones de
protones?.
7. Calcular las corrientes 1 e 2 en el circuito de la figura.
C
2. La carga total que entra por uno de los terminales de un
elemento de circuito vale  = (10 − 10−2 ) mC. Determinar la corriente en  = 05 s.
2A
4A
3. La corriente que fluye a través de un elemento es
½
2A
para 0    1
=
22 A
para   1
8. Obtener las corrientes 1 a 4 en el circuito de la figura.
4. La batería recargable de una linterna es capaz de
suministrar 85 mA durante 12 h. Si su tensión en los
terminales es 12 V, ¿Cuánta energía puede suministar?.
2A
I2
5. Determinar la potencia en cada elemento del circuito
de la figura y comprobar que se cumple el principio de
conservación de la energía.

2V 1
5V
2



3V 5
2A
4V
3

4
1V
5A
4A
9. Calcular la tensión  en el circuito de la figura.

2
6. Calcular las tensiones indicadas en el circuito de la
figura.

I3
3A
5A
3A

I4
7A
I1


A
3A
Calcular la carga que entra en el elemento entre  = 0 y
 = 2 s.

i2
i1
B
4V
 vx




4V



3V
10 V

5
1
v1
  v  
2
v3
4
10. Determinar la tensión AB en los siguientes circuitos.

8V



5V
(a)
1



10 V

8V
A
B
5V
(b)



10 V

8V
A
B
A
 10 V

5 V
(c)
B
15. Calcular la resistencia equivalente en cada uno de los
circuitos de la figura.
11. Calcular las tensiones 1 , 2 y 3 en el siguiente circuito.

15 V
A
6 k

2 k

25 V
 
10 V

20 V
1 k
 v2 



v1
v3
B
12. Calcular la corriente  y la tensión AB en el circuito
de la figura. Determinar la potencia consumida o
suministrada en cada elemento del circuito y realizar el
balance de potencia.
3
30 V
10 V


16. Calcular 1 , 2 y 3 en el circuito de la figura.
14 
40 V

(b)
(a)
5
A

12 k
1 k
B



2 k


 v1 
15 
I


VAB
12 k
4 k
A

v2

10 

v3

8V

17. Obtener la corrientes 1 a 5 en el circuito de la figura.
B
3
i1
13. Calcular la resistencia equivalente en el circuito de la
figura.
A
3
2
Req
40 V
4
6


i3
i2
i5
i4
4
1
2
5
4
3
1
B
18. Obtener  e  en el circuito de la figura.
i
14. En el circuito de la figura, determinar la resistencia
equivalente respecto de los terminales A-B, AB .
20 
A
RAB
5
8
18 
9A
9
20 
1
2
B
2

v

6S
4S
1S
2S
3S
19. En el circuito de la figura, obtener las corrientes 
e  , y la potencia disipada en la resistencia de 3 ohmios.
Soluciones:
1. 3204 × 10−13 C
2. 736 mA
20 
3
4
3. 667 C
5A
9A
6
13 
Ix
4. 44064 J
7
Iy
5. 1 = −4 W; 2 = 10 W; 3 = −20 W; 4 = 5 W;
5 = 9 W
6. 1 = 25 V; 2 = −5 V; 3 = 20 V
7. 1 = 7 A; 2 = −5 A
20. Calcular  e  en el circuito de la figura.

12 

12 V
v



8V
9.  = 15 V


 3 ix
ix
2V
8. 1 = 12 A; 2 = −10 A; 3 = 5 A; 4 = −2 A


10. (a) AB = 13 V; (b) AB = 7 V; (c) AB = −7 V
11. 1 = 35 V; 2 = 5 V; 3 = 30 V
12.  = 4 A; AB = 28 V
13. eq = 6 Ω
21. Obtener  en el circuito de la figura.
2 Vx

1
15 V


5
14. AB = 11 Ω
15. (a) eq =

Vx

8
11 KΩ
= 7273 Ω; (b) eq = 3 KΩ
16. 1 = 28 V; 2 = 3 = 12 V
17. 1 = 112 A; 2 = 16 A; 3 = 96 A; 4 = 64 A;
5 = 32 A
2
18.  = 6 A;  = 3 V
19.  = 163 A;  = 162 A; 3Ω = 1685 W
22. Para el circuito de la figura, calcular 0  en función
de , 1 , 2 , 3 y 4 . Si 1 = 2 = 3 = 4 , ¿para
qué valor de  resulta |0  | = 10?.
I0
Vs 

20.  = 10 V;  = −2 A
21.  = 4167 V
22.
R1
R2
 I0
R3
R4

V0

3
0
−3 4
=
,  = 40

(1 + 2 )(3 + 4 )