Perturbaciones y Clculo de Cortocircuitos
Anuncio

Perturbaciones y
Cálculo de Cortocircuitos Simétricos
Hortensia Amarís Duarte
Edgardo D. Castronuovo
1. Perturbaciones
Un ingeniero quiere que las cosas funcionen correctamente todo el tiempo. Sin embargo,
a veces esto no ocurre, y el sistema debe estar preparado para afrontarlo. Numerosas
causas pueden provocar fallos en el sistema:
•
Causas climáticas: un rayo puede caer en una torre de alta tensión, una
subestación de transformación puede inundarse, el viento puede acercar dos
conductores produciendo descargas eléctricas, etc.
•
Envejecimiento de los equipos: el aislante de los conductores disminuye su
eficiencia con los años, sucesivos ciclos de calentamientos y enfriamientos
varían las propiedades dieléctricas de los materiales, partes metálicas se
corroen, etc.
•
Otras causas: mala operación de los equipos, acción de animales, roturas por
obras de otras empresas, etc.
Independientemente de la causa que provoca el fallo, si el desperfecto es relativamente
importante provocará situaciones anormales en la operación. Entonces, los fallos en el
sistema serán observables como perturbaciones (más o menos bruscas) de los valores
medidos en situaciones normales de operación. Los valores habitualmente controlados
en un sistema eléctrico son: tensión, corriente, potencia y frecuencia. Así, podrán ser
detectadas las siguientes alteraciones:
Perturbaciones en los valores de tensión
Los equipos eléctricos son construidos para actuar con determinados niveles de tensión.
Por consiguiente, la banda permitida de variación en el módulo de la tensión es muy
acotada. La legislación especifica que son aceptadas, en general, variaciones máximas
de ± 5% en el valor nominal del nivel de tensión. Valores por encima o debajo de esa
banda pueden ocasionar daños en el equipamiento. Sub-tensiones (valores del módulo
de tensión inferiores al mínimo permitido de variación), cuando leves, pueden provocar
disminución de la vida útil y pérdida de eficiencia en los equipos. Sub-tensiones muy
inferiores al nivel nominal de tensión pueden provocar hasta la falla total permanente
del equipo eléctrico conectado a la red. Un motor, como ejemplo, requiere para
comenzar a girar una corriente de arranque bastante superior (entre 5 y 8 veces) a la
corriente normal de actuación. Cuando el motor intenta arrancar a una tensión inferior a
la nominal, la corriente de arranque puede ser varias veces superior a la normal de
actuación, pudiendo provocar hasta la quema del motor si no actúan equipos de
protección.
Las sobre-tensiones (valores del módulo de tensión superiores al máximo permitido de
variación) también pueden provocar daños en los equipos eléctricos. Como ejemplo,
una bombilla trabajando a una tensión levemente superior al rango de actuación
disminuye su vida útil en forma acentuada. Si la sobre-tensión es mayor, el aumento de
corriente asociado puede llevar a la quema de la bombilla.
Perturbaciones en los valores de corriente
Tres tipos de perturbaciones pueden ser asociadas a los valores de corriente: sobrecorrientes, cortocircuitos e inversión del sentido de la corriente.
•
Sobre-corrientes: son corrientes eléctricas levemente superiores a la nominal
(hasta 1.5 veces la corriente nominal, aproximadamente) que se mantienen por
tiempos relativamente largos. En general, los equipos eléctricos están diseñados
para soportar valores de corriente un poco superiores a los nominales, por lo que
las sobre-corrientes no producen generalmente la destrucción del equipo. Sin
embargo, los equipos que trabajan durante períodos prolongados en situaciones
cercanas a sus límites de operación sufren disminuciones apreciables en su vida
útil, ocasionando costos y aumentos en la tasa de fallo. Por consiguiente, esta
situación debe evitarse siempre que posible.
•
Cortocircuitos: desde el punto de vista eléctrico, cortocircuito es la conexión
accidental o intencionada, mediante una resistencia o impedancia relativamente
baja, de dos o más puntos de un circuito que están normalmente a tensiones
diferentes. Un cortocircuito origina aumentos bruscos en las corrientes
circulantes en una instalación, pudiendo dañar al equipamiento eléctrico,
equipos cercanos a la instalación y hasta personas no adecuadamente protegidas.
Algunos de los incidentes más graves en la instalación eléctrica pueden ser
representados por cortocircuitos: la caída de un rayo en una línea de transmisión,
el incendio de un transformador, la inundación de una sub-estación, etc. Dada la
gravedad de un cortocircuito, un análisis sistemático de este tipo de
perturbaciones será realizado en la sección siguiente, con el objetivo de detectar
y proteger a la instalación de los posibles daños asociados a los cortocircuitos.
•
Inversión del sentido de la corriente: en determinadas líneas del circuito,
puede conocerse que el sentido de la corriente eléctrica en operación normal
debe ser invariable. Por ejemplo, la corriente de un generador eléctrico debe ser
siempre saliente del mismo, pues entrega potencia al sistema. Cuando la
dirección de la corriente no es la que se prevé, estamos ante una perturbación en
el sentido de la corriente.
Perturbaciones en los valores de potencia
En el sistema eléctrico, instante a instante, deben mantenerse los balances de potencia
activa y reactiva. Como no es aún posible almacenar energía eléctrica en grandes
cantidades, el total de las potencias activa y reactiva consumidas deben ser producidas
en casi el mismo momento del consumo. El sistema está preparado para absorber y
controlar variaciones en la demanda (debidas a la aleatoriedad del consumo) y en la
generación o transmisión (ocasionadas por posibles fallas de equipos), dentro de ciertos
límites. Sin embargo, grandes desbalances entre las potencias producidas y consumidas
indican posibles desperfectos graves en el sistema de generación y transmisión de
energía eléctrica, que pueden llevar al corte de suministro en regiones o (mas grave aún)
en el total de la red. Así, el balance entre la producción y consumo de energía está
continuamente vigilado y controlado, a fin de detectar posibles perturbaciones.
Perturbaciones en los valores de frecuencia
En la sección anterior se dice que no hay forma de almacenar energía eléctrica en
grandes cantidades. Sin embargo, el sistema eléctrico almacena energía mecánica en la
masa girante de las máquinas que lo componen. Simplificando el concepto, la masa
girante en el sistema funciona como una reserva de energía, que puede extraerse cuando
necesario para satisfacer el balance de potencia activa. Así, cuando se presenta una
demanda no esperada en el sistema, la masa girante se desacelera entregando parte de su
energía cinética al sistema eléctrico. Al desacelerarse, disminuye consecuentemente la
frecuencia del sistema eléctrico. Lo contrario ocurre para una disminución no esperada
de la demanda, que puede llevar lleva a una aceleración de las masas girantes y un
aumento de la frecuencia del sistema. La masa girante presente en el sistema es muy
elevada, por lo que las variaciones en la frecuencia no deben ser proporcionalmente
importantes. Sin embargo, la relación entre la frecuencia del sistema y el balance de
potencia activa lleva a una vigilancia estrecha de los valores de frecuencia, que permite
detectar desbalances importantes entre la generación y demanda de energía.
2. Tipos de Cortocircuitos
Existen diferentes tipos de cortocircuitos, en función de las fases afectadas. Los
cortocircuitos pueden clasificarse en:
•
Trifásicos: consisten en el contacto de las tres fases, directamente o a través
de una impedancia de valor bajo. Un ejemplo de cortocircuito trifásico es la
caída de una torre de transmisión. Este tipo de cortocircuitos es el más grave
en el sistema, produciendo las mayores corrientes. Por consiguiente, debe ser
detectado rápidamente y eliminada la fuente de fallo del sistema (por medio
de la actuación del sistema de protección) en el plazo menor posible. Desde
el punto de vista de análisis, es el mas simple de ser calculado, porque al
estar involucradas las tres fases en la misma forma las corrientes de
cortocircuito son iguales en las tres fases, siendo representado por un sistema
de corrientes simétrico.
•
Bifásicos: los cortocircuitos bifásicos consisten en el contacto de dos fases
entre si. Como ejemplos de cortocircuito bifásico puede citarse: el roce de
dos fases en líneas aéreas y la falla de aislamiento puntual en cables aislados.
Este tipo de cortocircuito produce un sistema desequilibrado de corrientes,
con intensidades diferentes en las tres fases.
•
Bifásicos con contacto a tierra: en este tipo de cortocircuitos, dos de las
fases toman contacto entre sí y con la tierra en el punto de fallo. Es este el
tipo de cortocircuito estadísticamente menos frecuente.
•
Monofásico: el cortocircuito monofásico (contacto de una fase y tierra) es
responsable de la mayor cantidad de cortocircuitos en el sistema (en líneas
aéreas, 80% de los cortocircuitos son monofásicos). Las corrientes de
cortocircuito que provoca dependen de la impedancia de la falla y de las
conexiones a tierra de los transformadores en la línea.
De los cuatro tipos de cortocircuitos descriptos, solo el primero (trifásico) produce un
sistema de intensidades simétricas en las tres fases. A fin de calcularse las corrientes
circulantes por las fases en cortocircuitos bifásicos, bifásicos con contacto a tierra y
monofásicos se usará el método de las componentes simétricas.
Por ser el mas simple de estudiar y el que produce las condiciones mas críticas, será
estudiado en primer lugar el cortocircuito trifásico.
3. Cortocircuitos trifásicos
Los cortocircuitos trifásicos son los defectos que producen las mayores exigencias de
corriente en el sistema. Un cortocircuito trifásico que se prolongue en el tiempo puede
producir daños físicos en el equipamiento de la red (quema de transformadores,
generadores, etc.), que impidan reestablecer la entrega de electricidad en un plazo corto.
Por consiguiente, este tipo de cortocircuitos debe ser detectado y eliminado en el menor
tiempo posible. A fin de detectar que se ha producido un cortocircuito, se debe analizar
el circuito cuando se produce la falla y comparar las corrientes que se producen con el
defecto y en situación normal de funcionamiento. Cuando se produce un cortocircuito,
los equipos del sistema tienden a comportarse en una forma distinta a cuando están en
operación normal, debiéndose muchas veces utilizar otros modelos para su
representación.
Representación de generadores en situaciones de cortocircuito
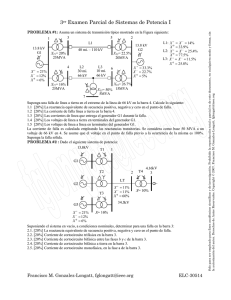
En situaciones normales, un generador sincrónico es generalmente representado (para el
análisis de sistemas eléctricos) como una fuente de tensión Ei en serie con una
impedancia Xd, como representado en la Fig. 1.a. Frente a situaciones de cortocircuito,
el campo magnético interno a la máquina se ve modificado, variando la impedancia
equivalente de la máquina generadora. Así, durante los primeros instantes después de la
falla (aproximadamente 5 segundos), la impedancia del generador sincrónico toma un
valor reducido, denominado de reactancia subtransitoria Xd’’ (modelo representado en la
Fig. 1.b). En el intervalo entre los 5 y 10 segundos después del cortocircuito, el
generador presenta un valor de reactancia de valor intermedio entre el de la reactancia
subtransitoria y a operación normal. A este valor intermedio se lo denomina de
reactancia transitoria Xd’, como representado en la Fig. 1.c. Después de los 10 segundos
después de la falla (este valor de tiempo depende del tipo de generador representado), el
generador sincrónico puede volver a ser representado por su modelo en operación
normal, como mostrado en la Fig. 1.a.
jXd’’
jXd
+
jXd’
+
Ei
+
Ei
-
Ei
-
(a)
-
(b)
(c)
Figura 1: Modelos de representación de los generadores sincrónicos ante cortocircuitos.
En la Fig. 1, debe recordarse que los valores de las reactancias para los modelos de
representación de los generadores sincrónicos siguen la regla Xd > Xd’ > Xd’’. Por
consiguiente, como la impedancia que presenta el generador en los primeros instantes
de la falla es mucho más reducida, el generador aporta al cortocircuito una corriente
más elevada que la que entregaría en condiciones normales de operación.
Representación de las cargas en situaciones de cortocircuito
Si el circuito posee motores o condensadores de gran tamaño (o sea, que consumen un
porcentaje relativamente grande de la potencia total consumida en el sistema), la energía
almacenada en estos elementos debe ser considerada. Durante la operación normal, las
bobinas y condensadores almacenan energía en sus campos magnéticos y eléctricos
(respectivamente), en un valor que depende de la corriente de pre-falla. Durante el
cortocircuito, estos elementos se descargan, devolviendo al sistema la energía
almacenada y aumentando en esta forma la corriente en la falta. Así, en los instantes
inmediatamente posteriores a un cortocircuito, motores y condensadores de gran tamaño
pueden ser representados como una fuente de tensión en serie con una impedancia. En
particular, los motores pueden ser representados en la misma forma usada para los
generadores para los períodos transitorio y subtransitorio, Figuras 1.b y 1.c.
Representación de las líneas de transmisión y distribución en
situaciones de cortocircuito
Las líneas de transmisión y distribución son representadas por impedancias o grupos de
impedancias, con valores y modelos de representación variantes con la longitud y el tipo
de línea. En general, no es considerada ninguna variación en la representación de la
línea para análisis de cortocircuitos trifásicos.
Cálculo de cortocircuitos trifásicos a través del Equivalente de
Thévenin.
En circuitos sencillos, la corriente de cortocircuito puede ser calculada usando el
Equivalente de Thévenin. Supóngase un circuito formado por un motor, representado
por una impedancia (Rm+jXm) conectado a un generador a través de una línea corta de
impedancia ZL, como mostrado en la Fig. 2.a. La Fig. 2.a puede corresponder a un
circuito monofásico o a un circuito monofásico equivalente de un generador con carga
balanceada.
Un cortocircuito puede ser representado por medio de un interruptor, que conecta dos
puntos A y B del sistema (en este caso, cercanos a los bornes del motor) a través de una
impedancia de falla ZF de pequeño valor, tal como es mostrado en la Fig. 2.b. Un valor
de impedancia ZF nulo caracteriza a un cortocircuito franco. Antes de cerrar el
interruptor, la tensión entre bornes del motor es EAB y no circula corriente por la rama
del interruptor. Al producirse el cierre del interruptor, los equivalentes del generador y
motor deben ser modificados. Como explicado en las secciones anteriores, el campo
magnético del generador es alterado por la acción del cortocircuito, adoptando la
tensión generada y la reactancia equivalente los valores subtransitorios Ei’’ y jXd’’,
respectivamente. El campo magnético del motor se ve también modificado por el
cortocircuito, por lo que debe considerarse el valor subtransitorio de la reactancia
equivalente, jXm’’. La energía almacenada en el campo magnético del motor (que va a
ser devuelta al sistema durante el cortocircuito) es representada a través de un generador
equivalente, de valor Em’’.
A
ZL
jXd
Rm
Ig
+
A
ZL
jXd’’
jXm’’
Im’’
’’
Ig
Rm
EAB
EAB
jXm
Ei
-
Ei’’
+
If’’
ZF
-
Em’’
-
B
(a)
+
B
(b)
Figura 2: Motor conectado a un generador, antes y durante el cortocircuito.
El circuito de la Fig. 2.b está constituido por 2 generadores y 4 impedancias, por lo se
puede analizar más fácilmente si se calcula el equivalente de Thévenin entre los puntos
A-B. El equivalente de Thévenin de un circuito consiste en un generador en serie con
una única impedancia, como mostrado en la figura 3.a. La tensión del generador del
equivalente Thévenin es la tensión medida a circuito abierto entre los bornes
considerados (en este caso, los puntos A-B) y la impedancia de Thévenin es calculada
como la impedancia equivalente observada entre los puntos considerados, cuando
pasivadas las fuentes independientes. En el circuito de la Fig. 2.b, para el interruptor
abierto (a circuito abierto), la tensión entre los puntos A-B tiende a mantenerse en el
valor EAB, valor igual al existente entre esos mismos puntos antes de considerarse el
cortocircuito (Fig. 2.a). El valor de tensión medido entre los puntos A-B antes de la falla
(llamado tensión de pre-falla) será entonces el valor de la tensión del generador de
Thévenin. En la figura 3.b se muestra el circuito equivalente, observado entre los bornes
A-B, cuando son pasivadas las fuentes independientes de tensión (Ei’’ y Em’’). La
impedancia del equivalente de Thévenin es calculada entonces como el paralelo entre la
impedancia subtransitoria del motor y la suma de las impedancias de línea y
subtransitoria del generador Zth=(Rm+j*Xm’’)//(ZL+j*Xd’’), como se muestra en la Fig.
3.c. En esta última figura se observan también las corrientes Ig’’ e Im’’, aportes a la
corriente de cortocircuito del generador y del equivalente del motor, respectivamente.
Zth
A
A
ZL
+
jXm’’
Eth
ZF
jXd’’
Rm
B
B
(a)
(b)
jXd’’
ZL
Ig’’
A
’’
Rm
+
EAB
jXd
Ig’’
-
ZF
B
(c)
Figura 3: Motor conectado a un generador, cálculo del equivalente de Thévenin.
Los valores de tensión del generador e impedancia del equivalente Thévenin, calculados
en los puntos A-B del circuito de la Fig. 2.a, son calculados en ecuaciones (1) y (2).
Eth = E AB
Z th =
(R
m
(1)
+ j ⋅ X m'' ) ⋅ ( Z L + j ⋅ X d'' )
Z L + Rm + j ⋅ ( X m'' + X d'' )
(2)
El método antes descrito es apropiado para el cálculo de las corrientes de cortocircuito
en circuitos simples, considerando o no las corrientes anteriores al cortocircuito (o
corrientes de pre-falla). Para circuitos más complejos, es difícil calcular el equivalente
de Thévenin en una forma directa. Por consiguiente, se usará para el cálculo de las
corrientes de cortocircuito la información contenida en la matriz Z de barras.
Cálculo de cortocircuitos trifásicos usando la matriz Z de barras.
La matriz de impedancias de barra (Z) puede ser calculada como la inversa de la matriz
de admitancias de barra (Y). La matriz Y se obtiene fácilmente de un circuito,
recordando que cada elemento no diagonal yij, i≠j, es la inversa de la impedancia física
⎛
1⎞
existente entre las barras i y j ( zij ), cambiado de signo, ⎜ yij = − ⎟ y los elementos
⎜
zij ⎠⎟
⎝
diagonales yii son obtenidos de la suma de las inversas de las impedancias zij
⎛
1
conectadas a la barra i ⎜ yii = ∑
⎜
zij
⎝
⎞
⎟⎟ .
⎠
Para calcular las corrientes y tensiones que se presentan en un sistema durante un
cortocircuito, considérese el sistema ejemplo representado en la Fig. 4.
1
2
3
ż12
+
żG1’’
ż23
4
VG1’’
-
żG2’’
5
ż14
ż45
+
VG2’’
-
ż53
żG3’’
+
VG3’’
-
Figura 4: Sistema mallado ejemplo.
La Fig. 4 muestra un circuito mallado con 3 generadores y 5 barras, para el que se busca
calcular las corrientes de cortocircuito. Como se quiere analizar la situación en régimen
subtransitorio, en la Fig. 4 son utilizados los equivalentes para este régimen. En la Fig. 4,
las tensiones Vi ,0 en las barras del sistema pueden ser calculadas usando la matriz de
impedancias de barra [Z] y el vector de inyecciones de corriente ⎡⎣ I i ,0 ⎤⎦ a través de la
ecuación ⎡⎣Vi ,0 ⎤⎦ = [ Z ] ⋅ ⎡⎣ I i ,0 ⎤⎦ . En una forma expandida, la ecuación anterior puede
escribirse como se muestra en (3).
⎡V1,0 ⎤ ⎡ z11
⎢V ⎥ ⎢
⎢ 2,0 ⎥ ⎢ z21
⎢V3,0 ⎥ = ⎢ z31
⎢ ⎥ ⎢
⎢V4,0 ⎥ ⎢ z41
⎢V5,0 ⎥ ⎢⎣ z52
⎣ ⎦
z12
z22
z32
z13
z23
z33
z14
z24
z34
z42
z53
z43
z54
z44
z55
z15 ⎤ ⎡ I1,0 ⎤
z25 ⎥⎥ ⎢ 0 ⎥
⎢ ⎥
z35 ⎥ ⋅ ⎢ I 3,0 ⎥
⎥ ⎢ ⎥
z45 ⎥ ⎢ I 4,0 ⎥
z56 ⎥⎦ ⎢⎣ 0 ⎥⎦
(3)
Se observa en la ecuación (3) que solo hay inyecciones de corriente en las barras 1, 3 y
4, debidas a los generadores G1, G2 y G3, respectivamente.
Cuando se produce un cortocircuito en la barra 5, con una impedancia de cortocircuito
zF , el sistema resulta en la Fig. 5.
1
2
3
ż12
+
żG1’’
ż23
4
VG1’’
-
żG2’’
5
ż14
ż53
+
VG2’’
-
ż45
+
żG3’’
VG3’’
-
żF
Figura 5: Sistema mallado ejemplo, después de cortocircuito en la barra 5.
Previo al cortocircuito, en la barra 5 había una tensión V5,0. Posteriormente al
cortocircuito, la tensión en la barra va a disminuir a un valor V5,5 (tensión en la barra 5,
debido a un cortocircuito en la barra 5). La tensión V5,5 puede ser calculada como el
''
producto de la corriente de falla IF,5’’ por la impedancia de falla zF , (V5,5 = I F,5
⋅ zF ) . El
cortocircuito puede simularse agregando a la barra 5 dos generadores ideales
adicionales, uno con la tensión anterior al cortocircuito V5,0, y otro en oposición con una
tensión VD,5 igual a la diferencia entre las tensiones previa y posterior al cortocircuito,
(VD,5 = V5,0 -V5,5 ) , como se muestra en la Fig. 6. Puede verificarse que la suma de los
(
)
dos generadores adicionales V5,0 + ( −VD,5 ) es la tensión V5,5, tensión de falla en la
barra 5.
1
2
3
ż12
+
żG1’’
VG1’’
-
ż23
4
ż14
ż53
ż45
+
VG3’’
-
żG3’’
żG2’’
5
+
VG2’’
-
IF,5’’
+
V5,0
VD,5
+
Figura 6: Sistema mallado ejemplo, después de cortocircuito en la barra 5, con generadores equivalentes
del cortocircuito.
Como la tensión V5,0 ya existía antes del cortocircuito, la acción del cortocircuito en
barra 5 es representada en la Fig. 6 solo por la adicción del generador VD,5, el cual
produce la corriente de falla IF,5’’. Aplicando superposición, se puede analizar el circuito
añadiendo a la situación anterior a la falla (ecuación (3)) la acción del generador VD,5,
como se muestra en la ecuación (4).
{
}
⎡⎣ ΔVi , j =5 ⎤⎦ + ⎡⎣Vi ,0 ⎤⎦ = [ Z ] ⋅ ⎡⎣ ΔI i , j =5 ⎤⎦ + ⎡⎣ I i ,0 ⎤⎦
(4)
En (4), ΔVi , j =5 es la variación en la tensión en la barra i debido a un cortocircuito en la
barra j=5, Vi ,0 es la tensión en la barra i, previa al cortocircuito, ΔI i , j =5 es la inyección
de corriente en la barra i, provocada por el cortocircuito en la barra j=5 e I i ,0 es la
inyección de corriente en la barra i, previa al cortocircuito. En particular, las
modificaciones en las tensiones de barra provocadas por el circuito pueden verse en la
ecuación (5) en una forma expandida.
⎡ ΔV1,5 ⎤ ⎡ z11
⎢ ΔV ⎥ ⎢
⎢ 2,5 ⎥ ⎢ z21
⎢ ΔV3,5 ⎥ = ⎢ z31
⎢
⎥ ⎢
⎢ ΔV4,5 ⎥ ⎢ z41
⎢
⎥
⎣ -VD,5 ⎦ ⎢⎣ z52
z12
z22
z32
z13
z23
z33
z14
z24
z34
z42
z53
z43
z54
z44
z55
z15 ⎤ ⎡ 0 ⎤
⎢
⎥
z25 ⎥⎥ ⎢ 0 ⎥
z35 ⎥ ⋅ ⎢ 0 ⎥
⎥
⎥ ⎢
z45 ⎥ ⎢ 0 ⎥
z56 ⎥⎦ ⎣⎢ − I ''F,5 ⎥⎦
(5)
De la ecuación (5), la corriente de falla IF,5’’ puede ser calculada como
''
I F,5
=
VD ,5
z55
(6)
y, como VD,5 = V5,0 -V5,5 , es
''
I F,5
=
''
V5,0 -V5,5 V5,0 - I F,5
⋅ zF
=
z55
z55
(7)
''
I F,5
=
V5,0
z55 + zF
(8)
o
Generalizando para un cortocircuito en una barra genérica j, resulta
I F,'' j =
V j ,0
z jj + zF
(9)
La ecuación (9) muestra que la corriente de cortocircuito en una barra es directamente
proporcional a la tensión en la barra previa al cortocircuito, e inversamente proporcional
a las impedancias de falla y diagonal de Z correspondiente a la barra en cortocircuito.
Cuando la impedancia de falla es nula (cortocircuito franco), se obtiene la máxima
corriente de cortocircuito en la barra, ecuación (10).
I MAX F, j =
''
V j ,0
(10)
z jj
La tensión en la barra de cortocircuito puede ser calculada a través de V j, j = I ''F, j ⋅ zF . De
(5), las variaciones de tensión en las otras barras i del sistema, debidas al cortocircuito
en j, son
ΔVi , j = − zij ⋅ I F,'' j = −
zij
z jj + zF
⋅V j ,0
(11)
Entonces, la tensión en la barra i después del cortocircuito será
Vi , j = Vi ,0 −
zij
z jj + zF
⋅V j ,0
(12)
Una aproximación bastante utilizada considera que las corrientes previas al cortocircuito
son mucho inferiores a las posteriores a la falla, y por consiguiente se desprecia su
efecto. Si se asume esta razonable simplificación, las tensiones previas a la falla en
todas las barras son iguales, e iguales a la tensión nominal en el circuito,
V1,0 = V2 ,0 = V3 ,0 = V4 ,0 = V5 ,0 = VN
(13)
Aplicando (13) en (12), resulta
⎛
zij
Vi , j = VN ⋅ ⎜ 1 −
⎜ z + z
jj
F
⎝
⎞
⎟⎟
⎠
(14)
En (14) se observa que las barras mas afectadas por el cortocircuito van a ser las que
tengan una alta impedancia equivalente zij entre la barra y el lugar donde ocurre el
cortocircuito.
La corriente subtransitoria que circula entre dos barras i y k (debida al cortocircuito en
la barra j) es calculada como la diferencia entre las tensiones de las dos barras
consideradas (después del cortocircuito), dividido por la impedancia real existente entre
estas barras, como se muestra en (15).
I ''i ,k =
Vi , j − Vk , j
V
=− N
zik
zik
⎛ z −z
⋅ ⎜ ij kj
⎜ z + z
⎝ jj F
⎞
⎟⎟
⎠
(15)
4. Bibliografía.
Análisis de Sistemas de Potencia, J. J. Graninger y W. D. Stevenson Jr., McGraw-Hill,
México, 1996.
Electrical power Systems. Design and Analysis, El-Hawary, M.E.:. IEEE Press, 1995.
Power System Relaying, Horowitz, S.H., Phadke, A.G.:. John Wiley & Sons, 1992.