apéndice Tasas de crecimiento Ejemplo : ¿Cuál ha sido el
Anuncio

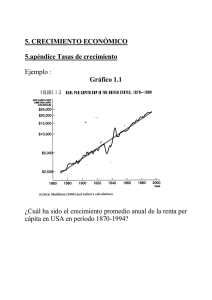
apéndice Tasas de crecimiento Ejemplo : ¿Cuál ha sido el crecimiento promedio anual de la renta per cápita en USA en período 1870-1994? Fórmula usual g x (%) = x t - x t -1 (∗ 100) x t -1 x t = x t -1 (1 + g x ) (1.1) (1.2) x t 2 − x t1 g x (promedio) = x t1 Δt En el ejemplo: 25000 − 2500 2500 g rpc = = 0.0726 = 7.26 % 124 (1.3) Tasa anual equivalente Si x crece todos los años a tasa g x constante: x t1 +1 = x t1 (1 + g x ) x t1 + 2 = x t1 (1 + g x ) 2 ..... x t 2 = x t1 (1 + g x ) Δt ⎛ x t2 gx = ⎜ ⎜ xt ⎝ 1 1/Δt ⎞ ⎟ ⎟ ⎠ -1 En el ejemplo: 1/ 124 ⎛ 25000 ⎞ g rpc = ⎜ ⎟ 2500 ⎠ ⎝ - 1 = 0.01874 = 1.874 % (1.4) Fórmula logarítmica Si x crece exponencialmente a tasa g x constante: x = x 0 eg x t ln x = ln x 0 + g x t gx = d(ln x) dt (1.5) (1.6) (1.7) Gráficamente, ln (x) = f(t) (escala semilogarítmica) es una recta de pendiente g x . Aplicando (1.5) en t1 y t 2 : x t1 = x 0 e g x t1 x t2 = x 0 e gxt2 dividiendo miembro a miembro la segunda ecuación por la primera y tomando logaritmos: gx = ln (x t 2 /x t1 ) Δt (1.8) En el ejemplo: ln (25000/250 0) = 0.01856 = 1.856 % gx = 124 que es la pendiente de la recta que une los puntos inicial y final en escala semilogarítmica. Ver gráfico pg. anterior ¿Cuánto tarda x en duplicarse?. Aplicando (1.8): gx = Δt = ln 2 Δt 70 ln 2 0.6931... 69.31... = = ≅ g x (%) g x (%) gx gx (1.9) (1.10) Tasas de crecimiento de operaciones. Aplicando (1.7) y las propiedades de los logaritmos: g (A/B) = g A - g B (1.11) g (A×B) = g A + g B (1.12) g (Aα ) = α g A , para α constante (1.13)