MHz 1.88 f ff = − = )10.(2 A 10 2 A P = ⇒ = = ∫ π + π )x
Anuncio

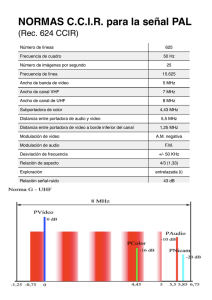
Primer Parcial. EC2422. Febrero 2005 (RESUELTO) TODO LO QUE UD. HAGA DEBE EXPLICARLO O DE LO CONTRARIO SE CONSIDERARA QUE LA RESPUESTA NO ES VALIDA Para todos los ejercicios de este examen se usarán mensajes xk(t) de audio, Ancho de Banda de 15Khz , máximo valor igual a 1v, potencia igual a 0.5 w. Problema 1: Suponga que en el aire solo existen emisoras FM cuyas frecuencias de portadora están entre 88.1 MHz y 107.9 MHz. Suponga que estas emisoras ocupan 200KHz y que la sensitividad de todos los moduladores es de 75000 Hz/v y que todas las señales a ser moduladas xk(t) (voz y música) cumplen las condiciones que están al comienzo de este examen. En el receptor mostrado en la figura de arriba, se conoce que fLO= 98.8 MHz , que la potencia a la salida del filtro IF es de 1 mw y que todos los filtros tienen ganancia unitaria. 1) ( 2 puntos)Cuál es la frecuencia de portadora de la emisora que se está escuchando? f c = f LO − f IF = 88.1MHz 2) ( 3 puntos)Escriba la expresión de la señal FM correspondiente a la emisora que está escuchando CON LUJO DE DETALLES (VALORES DE AMPLITUDES, FRECUENCIAS Y CONSTANTES PERFECTAMENTE DEFINIDOS). Esta expresión sería a la entrada del receptor SOLUCION: La señal FM de entrada al multiplicarse por 2Coseno se traslada pero no altera su amplitud. Como el filtro IF tiene ganancia unitaria a su salida se tiene una señal FM idéntica a la de entrada correspondiente a la emisora de 88.1MHz. Como la potencia a la salida del filtro IF es de 1mw, es porque A2 PIF = = 10 −3 ⇒ A = 2.(10 −3 ) 2 Finalmente la señal se representa como 2.(10 −3 )Cos(2 * π * 88.1 * 10 6 t + 2 * π * 75000∫ x ) En este problema el calcular A representa 2 de los 3 puntos asignados 3) ( 2 puntos)Si se quiere escuchar la emisora vecina superior, qué valor debe tener fLO. Justifíquelo Solución: La emisora vecina está distanciada de la de 88.1MHz en 200KHz, es decir tiene una frecuencia portadora de 88.3Mhz. Por lo tanto f LO = f c + f IF = 99MHz Problema 2: (6 puntos) En la figura se tiene que: a) El modulador FM tiene una sensitividad de 75000 Hz/v, una portadora de 1MHz y de potencia unitaria b) El modulador USSB tiene fo= 1.21 MHz 1) ( 4 puntos)Diseñe el filtro del modulador USSB, en detalle, a fin de que el modulador USSB funcione como tal La señal que ingresa al modulador USSB es una señal FM centrada en 1MHz y con un ancho de banda de 180KHz (Regla de Carson) o 200 KHz . Cuando se multiplica por el Coseno de f0, el espectro a la salida del multiplicador presenta (en magnitud) el siguiente aspecto: Para entender porque el USSB debe tener un determinado filtro observe lo que pasaría si la entrada del modulador USSB fuese una señal de energía con X(f) de forma triangular. Ubique la banda superior Por lo tanto el filtro pasabanda debe estar centrado en 2.21 MHz y debe tener como ancho de banda 180KHz o 210 KHz. 2) ( 2 puntos) Escriba una expresión lo mas detallada posible de la señal de salida Si uno observa la salida es otra señal FM que tiene otra frecuencia de portadora (2.21MHz),desviación igual a 75000 Hz/v, un desfasaje para el coseno de –pi/2 y una amplitud que es la de la señal FM original dividida entre 2. La señal FM original tiene una potencia de 1 w (igual a la de la portadora sin modular),por lo tanto su amplitud sería raíz de 2.Finalmente 2 Sen (2 * π * 2.21 * 10 6 t + 2 * π * 75000∫ x ) 2 Problema 3: (5 puntos) Una señal FM pasa por un demodulador ideal que produce a la salida y(t)= f∆ x(t)+ n(t) donde la DEP de n(t) es igual a Gn(f)=ηf2/2SR Para -0.5BT < f<0.5 BT donde BT es el ancho de banda de la señal FM. Si otro demodulador produce a la salida y1(t)= x(t) + n1(t) , determine la relación en dB entre la potencia del ruido n(t) y la potencia del ruido n1(t). EXPLIQUE Solución. Si un sistema ofrece una señal de y(t)= f∆ x(t)+ n(t) y el otro y1(t)= x(t) + n1(t), no queda ninguna duda de que y1(t)=y(t)/ f∆ Por lo tanto n1(t)=n(t)/ f∆ Y esto implica que DEP de n1(t) es DEP de n(t) dividida entre (f∆ )2. La relación entonces es: 10 log Pn = 10 log(f ∆ ) 2 = 97.5dB Pn1 Problema 4: (5 puntos) En la práctica 1 Ud. estudió el ruido pasabanda. Escriba todas las instrucciones con las cuales generó dicho ruido. Un ejemplo de lo esperado t=[1/10000:1/10000:1]; n=randn(size(t)); bpw=[.4 .6]; [a,b]=butter(15,bpw); nbp=filter(a,b,n); Podían usar en vez de butter, un filtro fir B = FIR1(N,Wn,'bandpass') Nbp=filter(1,B,n)