14_Anexo 2
Anuncio
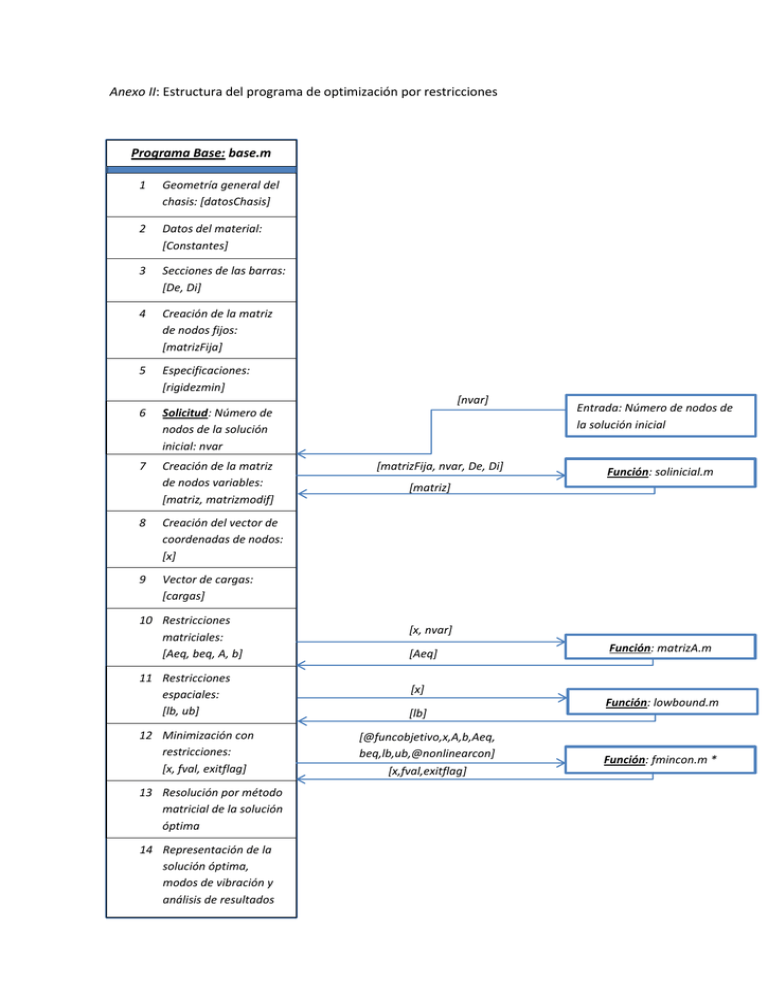
Anexo II: Estructura del programa de optimización por restricciones Programa Base: base.m 1 Geometría general del chasis: [datosChasis] 2 Datos del material: [Constantes] 3 Secciones de las barras: [De, Di] 4 Creación de la matriz de nodos fijos: [matrizFija] 5 Especificaciones: [rigidezmin] 6 Solicitud: Número de nodos de la solución inicial: nvar 7 Creación de la matriz de nodos variables: [matriz, matrizmodif] [nvar] 8 Creación del vector de coordenadas de nodos: [x] 9 Vector de cargas: [cargas] 10 Restricciones matriciales: [Aeq, beq, A, b] 11 Restricciones espaciales: [lb, ub] 12 Minimización con restricciones: [x, fval, exitflag] 13 Resolución por método matricial de la solución óptima 14 Representación de la solución óptima, modos de vibración y análisis de resultados [matrizFija, nvar, De, Di] Entrada: Número de nodos de la solución inicial Función: solinicial.m [matriz] [x, nvar] [Aeq] Función: matrizA.m [x] [lb] [@funcobjetivo,x,A,b,Aeq, beq,lb,ub,@nonlinearcon] [x,fval,exitflag] Función: lowbound.m Función: fmincon.m * Función de minimización: fmincon.m [x] Min f(x) Función: funcobjetivo.m [f(x)] Sujeto a: A·x ≤ b Aeq·x = beq [x] c(x) ≤ 0 Función: nonlinearcon.m ceq(x) = 0 Restricción de volumen lb(x) ≤ x ≤ ub(x) Restricción de longitud Restricción de rigidez Restricción de tensiones [c(x)] Restricción de frecuencias Restricción de volumen: Obtención de la zona “esférica” más cercana: [rad,rho] [x] Función: esferas.m [rad, rho] Restricción: 𝑐𝑣𝑜𝑙𝑢𝑚𝑒𝑛 = 𝜌𝑒 − 𝑑𝑖 𝜌𝑒 Restricción de longitud: Obtención de la longitud de cada barra: [longitud(x)] Restricción: 𝑐𝑙|𝑚𝑖𝑛 = 𝑙𝑚𝑖𝑛 − min(𝑙𝑖 ) 𝑙𝑚𝑖𝑛 𝑐𝑙|𝑚𝑎𝑥 = max(𝑙𝑖 ) − 𝑙𝑚𝑎𝑥 𝑙𝑚𝑎𝑥 [x] [longitud(x)] Función: longitud.m Restricciones de rigidez, tensiones y frecuencias de vibración: Obtención de la rigidez de la estructura: 𝐾= 𝐾𝑚𝑖𝑛 − 𝐾 𝐾 Obtención de la máxima tensión en la estructura: 𝜎𝑒𝑞 = 𝜎 2 + 3𝜏 2 Restricción: 𝑐𝑡𝑒𝑛𝑠𝑖ó𝑛 = 𝜎𝑚𝑖𝑛 − 𝜎𝑒𝑞 𝜎𝑚𝑖𝑛 Obtención de la mínima frecuencia natural Restricción: 𝑐𝑓𝑟𝑒𝑐 = Función: matricial.m 1 𝛿𝑚 Restricción: 𝑐𝑟𝑖𝑔𝑖𝑑𝑒𝑧 = [matriz,constantes,cargas,n] 𝜔𝑚𝑖𝑛 − 𝜔𝑛 𝜔𝑚𝑖𝑛 [Reacciones,Fuerzas,desp,KglobalTotal,nodes,matriz, MglobalTotal,plocales,numbarras,natfreq,modes] Función: matricial.m 2 Obtención longitudes de las barras 3 Matrices locales de rigidez y masa 4 Matrices de cambio de base 5 Matrices locales de rigidez y masa en coordenadas globales 6 Ensamblaje de las matrices en coordenadas globales 7 Obtención de desplazamientos y modos provisionales 8 Matriz de rigidez y masa reducidas 9 Vector reducido de desplazamientos y fuerzas [x] Función: longitud.m [longitud(x)] [E,G,A,L,Iy,Iz,It] Funciones: klocal.m, mlocal.m [klocales, mlocales] [nodos] Funciones: Tab.m, Tba.m [Tab,Tba] 𝑇 𝐾 = 𝑇𝑎𝑢𝑥 𝑇𝑝𝑇 𝑘𝑇𝑝 𝑇𝑎𝑢𝑥 [kglobal, mglobal ,posiciones] Función: ensamblaje.m [Kglobal,Mglobal] [Kglobal,Mglobal] Función: reducida.m [Kreduc ,Mreduc] [desp,P] ] [despreduc,Preduc] Función: despreducida.m 10 Resolución del sistema: 𝑃 = 𝐾Δ 12 Obtención de desplazamientos, fuerzas y reacciones 11 Obtención de esfuerzos locales en barras 𝑝𝑎𝑏,𝑝 … 𝑝𝑏𝑎,𝑝 = 𝑏 𝑘𝑎𝑎,𝑝 ⋯ 𝑘𝑏𝑎,𝑝 … ⋯ ⋯ 𝑘𝑎𝑏,𝑝 ⋯ 𝑎 𝑘𝑏𝑏,𝑝 𝛿𝑏𝑎,𝑝 … 𝛿𝑏𝑎,𝑝






