Adición Términos como juntar, agregar, buscar totales, son claves
Anuncio
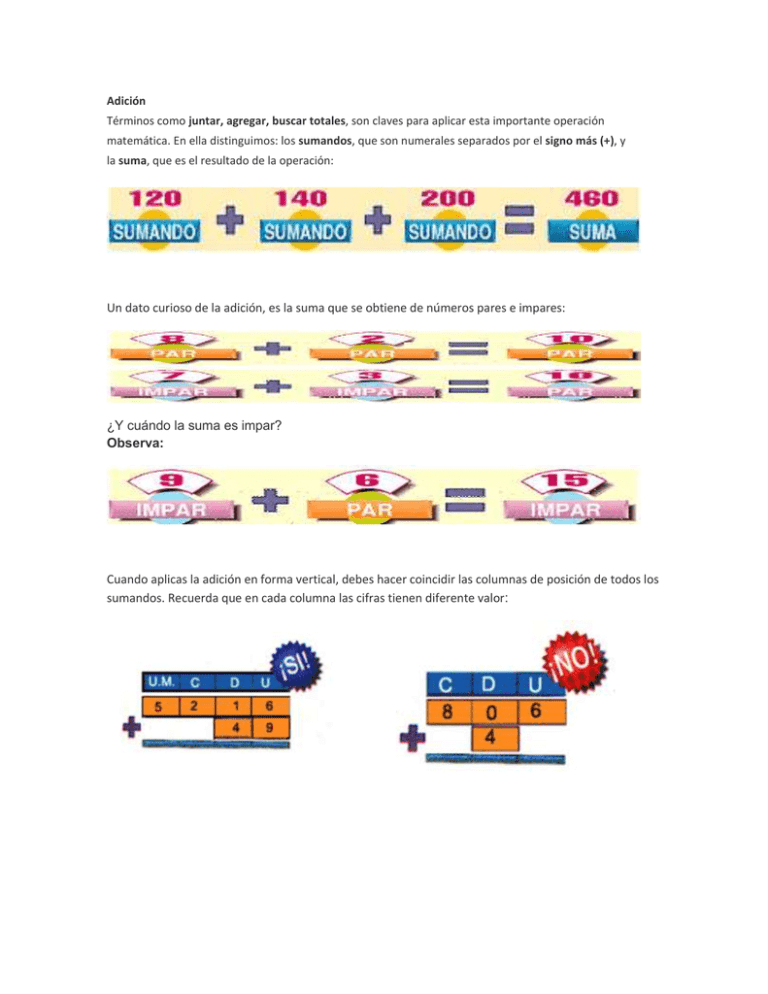
Adición Términos como juntar, agregar, buscar totales, son claves para aplicar esta importante operación matemática. En ella distinguimos: los sumandos, que son numerales separados por el signo más (+), y la suma, que es el resultado de la operación: Un dato curioso de la adición, es la suma que se obtiene de números pares e impares: ¿Y cuándo la suma es impar? Observa: Cuando aplicas la adición en forma vertical, debes hacer coincidir las columnas de posición de todos los sumandos. Recuerda que en cada columna las cifras tienen diferente valor: Sustracción ¡Cuántas veces decimos: me queda, me falta, la diferencia...! Ahí nos referimos a la sustracción, una operación que tiene como elementos: Cuántas veces decimos: me queda, me falta, la diferencia...! Ahí nos referimos a la sustracción, una operación que tiene como elementos: La sustracción no es cerrada, porque no siempre tiene solución en los números cardinales: 3 - 12 =? Sólo se puede resolver cuando el minuendo es mayor o igual que el sustraendo. Tenemos la siguiente sustracción: 12 - 3 = 9. Pero, ¿por qué es 9? Porque 9 + 3 = 12. Entonces, la sustracción es la operación inversa a la adición. Por eso, para comprobar si la diferencia está correcta, sumamos la resta, más el sustraendo y debemos obtener el minuendo. Veamos el siguiente ejemplo: 425 - 55 = 370 Si esta sustracción es correcta, debe darse lo siguiente: 370 + 55 = 425 Como la suma es correcta, entonces el resultado de la sustracción también es correcto. Cuando aplicas la sustracción en forma vertical, debes hacer coincidir las columnas de posición del minuendo y el sustraendo. Recuerda que en cada columna las cifras tienen diferente valor: Sustracción con reserva: Primero debes saber reconocer cuándo la resta será con reserva (o con prestado, diremos mejor). Observa cómo se restan números cuando algunos de los números de la cifra de arriba son menores que los de abajo. Cuando esto sucede debes seguir los siguientes pasos: Primero debes saber reconocer cuándo la resta será con reserva (o con prestado, diremos mejor). Observa cómo se restan números cuando algunos de los números de la cifra de arriba son menores que los de abajo. Cuando esto sucede debes seguir los siguientes pasos: Observa el ejemplo: el número (la cifra) 472, está compuesto del 4, del 7 y del 2. El 2 representa 2 unidades, el 7 representa 7decenas y el 4 representa 4 centenas. Cada decena tiene 10 unidades. Ahora observa el número de abajo de la resta, el 145. Está compuesto del 1, del 4 y del 5. El 5 son las unidades, el 4 representa 4decenas y el 1 representa 1 centena. Cómo se resta. Siempre se empieza restando los números desde la derecha. En este caso será 2 menos 5. Como 2 es menor que 5 no podemos hacer una resta. ¿Qué hacemos, entonces? El 2 de arriba es VECINO con el 7 y con él forman el 72. Como son amigos, el 2 le pide prestado un 1 (una decena) al 7. El 7 le presta un 1 y él se queda convertido en 6, pero su amigo el 2 ahora puede colocarse un 1 adelante y se convierte en 12. En este momento podemos restar 12 menos 5, lo que es igual a 7. El número de la izquierda es ahora el 6 (que antes era 7 pero prestó 1) y el de abajo sigue siendo 4. Y decimos, 6 menos 4 es igual a 2. La resta resuelta queda de la siguiente manera: - 6 12 4 7 2 1 4 5 -3 -2 -7 Resuelve ahora las siguientes restas. Recuerda que cuando un número de arriba es menor que uno de abajo, debes pedir prestado 1 al número de la izquierda (es como pedir prestado dinero). 893 - 548 ---------- 765 - 527 --------- 526 - 218 --------- 340 - 225 --------- 374 - 146 --------- 832 - 321 --------- 743 - 532 --------- 964 -653 ---------- Ejercicios de adiciones y sustracciones. http://www.rmm.cl/usuarios/ereye/doc/SUMAS%20CON%20RESERVA%20y%20RESTAS%20CON% 20CANJE.pdf Aprende Las Fracciones Las fracciones corresponden a la división de una totalidad en partes iguales, como cuando dividimos un pastel en dos partes iguales o cuando hablamos de un cuarto de una hora. Concepto de fracción Se ha dividido el rectángulo en cuatro partes iguales y se ha sacado un cuarto del rectángulo. El denominador indica la cantidad de partes en que se ha dividido el entero, en este caso 4, y el numerador, la cantidad de esas partes del entero que se han considerado, en este caso 1. Para leer una fracción, el numerador se lee normalmente pero, como veremos a continuación, el denominador tiene una forma especial de leerse. Denominador Lectura Ejemplos 2 medios 5 / 2 = cinco medios 3 tercios 2 / 3 = dos tercios 4 cuartos 3 / 4 = tres cuartos 5 quintos 4 / 5 = cuatro quintos 6 sextos 5 / 6 = cinco sextos 7 séptimos 6 / 7 = seis séptimos 8 octavos 7 / 8 = siete octavos novenos 8 / 9 = ocho novenos 10 décimos 9 / 10 = nueve décimos mayor de 10 Se agrega al número la terminación avos 10 / 11 = diez onceavos 9 Clasificación De Las Fracciones Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes. Tipo Características Ejemplos Propia El numerador es menor que el denominador 1 / 2, 7 / 9 Impropia El numerador es mayor que el denominador 4 / 3, 5 / 2 Homogéneas Tienen el mismo denominador 2 / 5, 4 / 5 Heterogéneas Tienen distinto denominador 3 / 7, 2 / 8 Entera El numerador es igual al denominador; representan un entero 6/6=1 Cuando tienen el mismo valor. Dos fracciones son equivalentes si son iguales sus productos cruzados Equivalentes 2/3y4/6 2x6=3x4 Suma Y Resta De Fracciones Si las fracciones tienen el mismo denominador (homogéneas), se suman o restan los numeradores y se pone el mismo denominador. Ejemplo: 3 — 2 + 6 — (3 + 2) = 6 ——— 5 = 6 — 5 — ; 6 (5 – 2) 2 – 7 — = 7 3 ——— = 7 — 7 Si las fracciones tienen distinto denominador (heterogéneas), lo primero que tenemos que hacer es igualar los denominadores. Para conseguirlo, buscamos dos fracciones equivalentes a las dadas, multiplicando el numerador y el denominador de cada una de ellas por el denominador de la otra. Una vez obtenido el mismo denominador, procedemos como en el caso anterior, sumamos los numeradores y ponemos el denominador común. Ejemplo: 2 — 5 3 + — 7 (2 x 7) = ——— (5 x 7) (3 x 5) + ——— (7 x 5) 14 = —— 35 15 + —— 35 29 = —— 35 Tipos de representaciones: Las fracciones pueden representarse en regiones o conjuntos Representación grafica de una fracción dada: Cuando se quiere representar una fracción mediante un dibujo, se pueden utilizar dos formas; se pueden representar con un diagrama (un circulo o cuadrado, etc.)o mediante subconjuntos en un conjunto. Esta forma de representar las fracciones utiliza una figura geométrica; las figuras mas usadas son el círculo, el cuadrado, el rectángulo y el triangulo. Cualquiera sea la figura debe dividirse en partes iguales. El total de partes dependerá del denominador, ya que esta indica las partes que se tomaron del entero. Las partes del dibujo que se pintarán dependerán del numerador, porque éste indica las partes que se toman del entero. Hagamos algunos ejemplos: Figuras geométricas Una figura geométrica es un conjunto no vacio cuyos elementos son puntos. Estas figuras entendidas como lugares geométricos son áreas cerradas por líneas o superficies en un plano o en el espacio. Las figuras geométricas de lados rectos se denominan polígonos y las figuras de lados curvos se denominan círculo y circunferencia y corresponden también a polígonos. Las figuras geométricas planas son aquellas regiones cerradas por líneas no alineadas en un plano de dos dimensiones. Estas figuras geométricas planas se clasifican principalmente en dos tipos dependiendo de si sus líneas curvas o rectas: Cónicas son las figuras geométricas planas delimitadas por una línea curva cerrada y plana que resultan de la intersección no degenerada entre un cono y un plano que no pasa por su vértice. Por ejemplo el círculo y la elipse. Polígonos son las figuras geométricas planas delimitadas por el cruce de dos o más líneas rectas, con tres o más lados e igual cantidad de ángulos. http://arte.about.com/od/Que-es-el-arte/fl/Figuras-geometricas.htm Según las características de las figuras geométricas (polígonos) se pueden establecer varias clasificaciones. Según la medida de sus lados y ángulos, los polígonos pueden ser regulares e irregulares. Un polígono es regular si todos sus lados poseen la misma longitud y si todos sus ángulos son iguales. Ejemplos: Polígonos regulares Un polígono es irregular si todos sus lados tienen longitudes diferentes al igual que la medida de sus ángulos. Ejemplos: Lados diferentes Ángulos diferentes De acuerdo con sus ángulos interiores, los polígonos pueden ser convexos y cóncavos. Un polígono es convexo cuando todos sus ángulos interiores son menores a 180° Ejemplo: En el polígono ABCDE cada uno de sus ángulos interiores es menor de 180º Un polígono es cóncavo, si tiene al menos un ángulo interior mayor de 180 ° Ejemplo: El ángulo interior T del polígono RSTU es mayor de 180ª Ahora bien, según el número de lados que posean (el número de lados es igual al número de ángulos que tiene la figura) los polígonos se pueden clasificar de la siguiente manera: Nombre Número de lados Triángulo 3 Cuadrilátero 4 Pentágono 5 Hexágono 6 Heptágono 7 Octágono 8 Eneágono 9 Decágono 10 Undecágono 11 Dodecágono 12 Los demás polígonos simplemente se nombran indicando el número de lados que lo forman; polígono de trece lados, de catorce lados, etc., a excepción del polígono de veinte lados que también recibe un nombre específico (icosígono). Triángulos Veamos en seguida lo referente al polígono de tres lados, llamado triángulo. Los triángulos se clasifican según la medida de sus lados en: Triángulo equilátero: el que tiene sus 3 lados iguales. Triángulo isósceles: el que tiene 2 de sus lados de igual medida. Triángulo escaleno: el que tiene sus 3 lados de distinta medida. Los triángulos también se pueden clasificar según la medida de sus ángulos en: Triángulo acutángulo: el que tiene sus 3 ángulos agudos (menores de 90º) Triángulo rectángulo: el que tiene 1 ángulo recto (90º) Triángulo obtusángulo: el que tiene 1 ángulo obtuso (mayor de 90º y menos que 180º) Cuadriláteros Otro de los polígonos muy populares son los cuadriláteros, los cuales se clasifican en: Paralelógramos: son aquellos que tiene 2 pares de lados paralelos (cuadrado, rectángulo, rombo y romboide) Trapecios: son aquellos que tienen 1 par de lados paralelos Trapecio isósceles: 2 lados de igual medida, 2 ángulos basales iguales Trapecio trisolátero: 3 lados de igual medida, 2 pares de ángulos basales iguales Trapecio rectángulo: ángulos basales rectos (90º) Trapecio escaleno: lados y ángulos de distinta medida Trapezoides: No tienen lados paralelos Trapezoide simétrico: 2 lados de igual medida Trapezoide asimétrico: todos los lados de distinta medida Conocer las características de los polígonos ayuda para el estudio de muchos temas como perímetros y áreas entre otros. Cuerpos geométricos: Elementos de un cuerpo geométrico - Caras: son las superficies planas que limitan el cuerpo geométrico. Estas superficies planas son figuras geométricas. Las caras basales son las que sirven para apoyar el cuerpo en el plano. Las otras caras se llaman laterales. - Aristas: son las líneas que se forman cuando se juntan dos caras. Se puede decir también, que son los lados de las figuras geométricas que forman los lados del cuerpo. (Figura 2) - Vértices: son los puntos donde se juntan tres o más caras. (figura 3) Prismas Son cuerpos cuyas caras laterales son cuadrados o rectángulos y cuyas bases son paralelas, pudiendo ser cualquier polígono (cuadrado, triángulo,etc) y el segmento que une los centros de las bases (llamado altura) mide lo mismo que la arista (lateral) Cubo: Cuerpos que están formados por 6 cuadrados. Según su base se llaman: Poliedro Triangular Poliedro Pentagonal Poliedro Cuadrangular Poliedro Hexagonal Otros cuerpos geométricos: Pirámides Cuerpos redondos