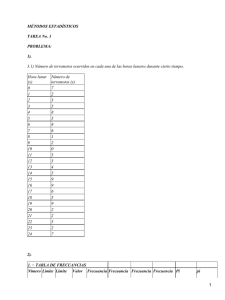
Medida armónica y medida geométrica Andrea Arrazquito Gaitán La
Anuncio

Medida armónica y medida geométrica Andrea Arrazquito Gaitán La media armónica, denominada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores Así, dados los números a1,a2, ... , an, la media armónica será igual a: Propiedades 1. La inversa de la media armónica es la media aritmética de los inversos de los valores de la variable. 2. Siempre se puede pasar de una media armónica a una media aritmética transformando adecuadamente los datos. Ventajas Considera todos los valores de la distribución y en ciertos casos, es más representativa que la media aritmética. Desventajas La influencia de los valores pequeños y El hecho que no se puede determinar en las distribuciones con algunos valores iguales a cero; por eso no es aconsejable su empleo en distribuciones donde existan valores muy pequeños. La media geométrica de una cantidad arbitraria de números (digamos n números) es la raíz n-ésima del producto de todos los números. Propiedades El logaritmo de la media geométrica es igual a la media aritmética de los logaritmos de los valores de la variable. Ventajas: considera todos los valores de la distribución y es menos sensible que la media aritmética a los valores extremos. Desventajas: es de significado estadístico menos intuitivo que la media aritmética, su cálculo es más difícil y en ocasiones no queda determinada; por ejemplo, si un valor xi=0 entonces la media geométrica se anula. Solo es relevante la media geométrica si todos los números son positivos. Como hemos visto, si uno de ellos es 0, entonces el resultado es 0. Si hubiera un número negativo (o una cantidad impar de ellos) entonces la media geométrica sería o bien negativa, o bien inexistente en los números reales. En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal. La media geométrica es relevante cuando varias cantidades son multiplicadas para producir un total. Media geométrica ponderada Al igual que en una media aritmética pueden introducirse pesos como valores multiplicativos para cada uno de los valores con el fin de ponderar o hacer pesar más en el resultado final ciertos valores, en la media geométrica pueden introducirse pesos como exponentes: Desventajas: es de significado estadístico menos intuitivo que la media aritmética, su cálculo es más difícil y en ocasiones no queda determinada; por ejemplo, si un valor xi=0 entonces la media geométrica se anula Media geométrica ponderadaAl igual que en una media aritmética pueden introducirse pesos como valores multiplicativos para cada uno de los valores con el fin de ponderar o hacer pesar más en el resultado final ciertos valores, en la media geométrica pueden introducirse pesos como exponentes: medidas geometricas es la raíz n-ésima del producto de todos los números. propiedades El logaritmo de la media geométrica es igual a la media aritmética de los logaritmos de los valores de la variable. Ventajas • Considera todos los valores de la distribución y • en ciertos casos, es más representativa que la media aritmética. Desventajas Propiedades •La influencia de los valores pequeños y •El hecho que no se puede determinar en las distribuciones con algunos valores iguales a cero; por eso no es aconsejable su empleo en distribuciones donde existan valores muy pequeños. •La inversa de la media armónica es la media aritmética de los inversos de los valores de la variable. •Siempre se puede pasar de una media armónica a una media aritmética transformando adecuadamente los medida armonica datos. La media armónica, denominada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores