PROBLEMA RESUELTO No 2 Un condensador de placas paralelas

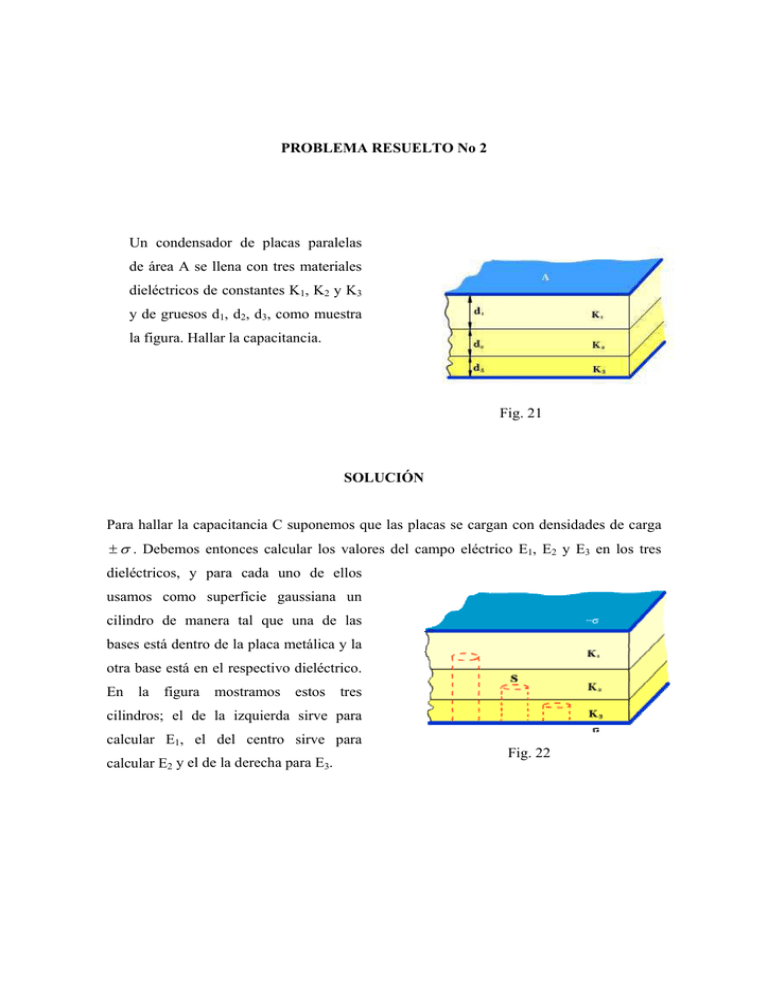
PROBLEMA RESUELTO No 2
Un condensador de placas paralelas
de área A se llena con tres materiales
dieléctricos de constantes K1, K2 y K3
y de gruesos d1, d2, d3, como muestra
la figura. Hallar la capacitancia.
Fig. 21
SOLUCIÓN
Para hallar la capacitancia C suponemos que las placas se cargan con densidades de carga
± σ . Debemos entonces calcular los valores del campo eléctrico E1, E2 y E3 en los tres
dieléctricos, y para cada uno de ellos
usamos como superficie gaussiana un
cilindro de manera tal que una de las
bases está dentro de la placa metálica y la
otra base está en el respectivo dieléctrico.
En la figura mostramos estos tres
cilindros; el de la izquierda sirve para
calcular E1, el del centro sirve para
calcular E2 y el de la derecha para E3.
Fig. 22
Calculemos por ejemplo Ε 2 :
El flujo del desplazamiento es Ε 2ε 2 S , y la carga libre encerrada es σS , entonces la
ley de Gauss dice que E2 ε 2 S = σ S , de donde obtenemos E2 =
E2 =
E1 =
σ
K 2ε 0
. De la misma manera se calculan E1, y E3 para obtener :
σ
;
K 1ε 0
E2 =
σ
K 2ε 0
;
E3 =
σ
K 3ε 0
;
La caída de potencial en el material K1 es ∆ V1 = E1d1 =
∆V2 =
σ
σ
,
=
ε 2 K2ε0
(1)
σ d1
; así mismo
K1ε 0
σ d3
σ d2
y ∆V3 =
, y la diferencia de potencial entre las dos placas
K 2ε 0
K3ε 0
conductoras es ∆ V = ∆ V1 + ∆ V2 + ∆ V3 =
∆V =
Finalmente,
C=
C=
σ d1
σ d2
σ d3
+
+
:
ε 0 K1 ε 0 K 2 ε 0 K 3
σ  d1 d 2 d3 

 ;
+
+
ε 0  K1 K 2 K3 
ca rga σA
=
:
∆V
∆V
ε0 A
d1 d 2 d 3
+
+
K1 K 2 K 3
Para el condensador del problema anterior:
a).
(2)
Calcule la energía total contenida en él.
(2)
b).
Calcule la energía del campo eléctrico en cada uno de los tres
materiales dieléctricos.
c).
Sume las tres contribuciones de la respuesta b) y compare con la
respuesta a).
a) Designando por ET la energía total tendremos:
Q 2 (σΑ )2 Aσ 2  d1 d 2 d3 


ET =
=
=
+
+
2C
2C
2ε 0  K1 K 2 K3 
b) En el medio K1 la densidad volumétrica de energía es
1
ε 1 E12 ; como este
2
material K1 tiene volumen Ad1 entonces la energía, Em1, del campo eléctrico en el
medio K1 es Em1 =
Em1 =
1
ε 1 E12 Ad1 , y al usar el resultado (1) anterior tendremos que:
2
σ 2 A d1
.
2ε 0 K1
Así mismo las energías de los campos eléctricos en los medios K2 y K3 serán:
σ 2 A d2
Em2 =
2ε 0 K 2
y
σ 2 A d3
Em3 =
2ε 0 K3
c) Finalmente sumamos estas tres contribuciones:
Aσ 2  d1 d 2 d3 

 ,
Em11 + Em2 + Em3 =
+
+
2ε 0  K1 K 2 K3 
que coincide con la respuesta del literal a). Hemos verificado, pues, que la
“energía contenida en un condensador” es la energía del campo eléctrico.