Material realizado por la Prof.: Leticia Barrios

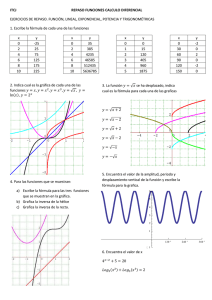
FUNCIONES Y GRAFICAS
Al estudiar los fenómenos que se producen en la naturaleza, se observa que en ellos hay dos o más magnitudes
relacionadas entre sí, significa que al variar una de las magnitudes, la otra también cambia. Por ejemplo la longitud de
una varilla de acero aumenta cuando se eleva su temperatura; la fuerza que un imán ejerce sobre un clavo disminuye a
medida que aumenta la distancia entre ambos, etc.
Las magnitudes están relacionadas, y se dice que una es función de la otra, la longitud de la varilla es función de la
temperatura y se escribe l=f (T); la fuerza del imán es función de la distancia y se escribe F=f (d).
Existen varios tipos de funciones que relacionan las magnitudes, algunas de ellas:
-proporción directa
-variación lineal
-variación no lineal
-relaciones inversas
PROPORCION DIRECTA
Cuando dos magnitudes están relacionadas de modo que al duplicar el valor de una de ellas también se duplica el valor
de la otra; al triplicar la primera, la segunda también aumenta el triple, y así sucesivamente.
Por ejemplo, si medimos la masa de bloques de hierro de distintos volúmenes, tendríamos
Observemos como es la relación entre el volumen y la masa, “la masa del bloque es directamente proporcional al
volumen que ocupa esa masa”, esto se puede expresar por medio de símbolo (α), de la siguiente manera M α V.
Si le buscamos cuantitativamente la relación entre la masa y el volumen (M/V: 8g/1cm 3, 16g/2 cm3, etc.) encontramos
que nos da siempre el mismo resultado 8g/ cm3, podemos decir que esa relación es constante (M/V=K).
K es la constante de proporcionalidad entre Mi, entonces K= 8g/ cm3.
Otro ejemplo: una persona al recoger el agua que sale de una manguera obtiene los siguientes datos:
t(s)
5
10
30
V(L)
15
30
90
Si buscamos la relación entre el volumen expresado en litros y el tiempo en segundos, podemos decir que es
directamente proporcional V α t y el valor de K= 3L/s
Si graficamos M=f (V), en el primer ejemplo, obtendremos:
La grafica que representa una magnitud que varía en proporción directa respecto de otra es una línea recta que pasa
por el origen
¿Cómo podemos determinar el valor de K a través de la grafica?
Material realizado por la Prof.: Leticia Barrios
La pendiente o inclinación de la recta se define: pendiente=∆M/∆V;
Por lo que la pendiente=K.
Podemos escribir la función correspondiente a la grafica M=f(V)
M=K.V ;CUANDO M=0, V=0
Siendo K, la constante de proporcionalidad.
Corresponde a una ecuación de primer orden
VARIACION LINEAL
En el caso anterior la recta pasa por el origen, enK otros caso esto puede no suceder, cuando X=0, Y≠0.
Si
Si graficamos L=f (M) obtendremos una grafica rectilínea que no pasa por el origen, ambas variables están relacionadas
por una variación lineal; L varia linealmente con M.
En la primera grafica vemos que cuando M=0, L=6; la pendiente es K.
En la segunda grafica L puede ser Y, M puede ser X y K puede ser a; la
relación matemática es Y=aX+b , siendo b el valor de Y para X=0.
VARIACION NO LINEAL
(CUADRATICA O CUBICA)
Variación proporcional al cuadrado. Tomaremos como ejemplo el área del cuadrado A=L2
Cuando L=1m, A=1m2; L=2m, A=4m2 ; L=3m, A=9m2
Al duplicar L, A aumenta 4veces; al triplicar L, A aumenta 9 veces , etc.
AαL2 , y la grafica A=f(L)tiene forma de PARABOLA.
AαL2, A=K.L2
Material realizado por la Prof.: Leticia Barrios
Variación proporcional al cubo. Tomaremos como ejemplo el volumen del cubo
V=L3
V α L3 . Si graficamos V=f(L), la curva es semejante a la anterior, pero no es una
simple parábola, muestra una inclinación más pronunciada conforme aumenta L
V=K.L3
PROPORCIONES INVERSAS
Cuando una magnitud aumenta la otra disminuye.
Proporción inversa. Dos magnitudes X e Y tales que al duplicar X el valor de Y queda dividido entre dos; al triplicar X el
valor de Y se divide en tres, asi sucesivamente.
“Y es inversamente proporcional a X” o “Y es directamente proporciónal al inverso de X”
Y α ⅟X
Al introducir la constante de proporcionalidad K, la función es Y=K(⅟X) o Y= K/X
la representación grafica es:
Variación con el inverso del cuadrado. Es el caso que cuando al duplicar X, el valor deY disminuye 4veces; al triplicar X,
el valor de Y disminuye 9 veces, etc.
Decimos que “Y es inversamente al cuadrado de X ” o “Y es proporcional al inverso del cuadrado de X ”
Yα⅟X2 al introducir la constante de proporcionalidad K ; Y=K(⅟X2) o Y=K/X2
La representación grafica es:
Material realizado por la Prof.: Leticia Barrios