estructuras trianguladas - flexion
Anuncio
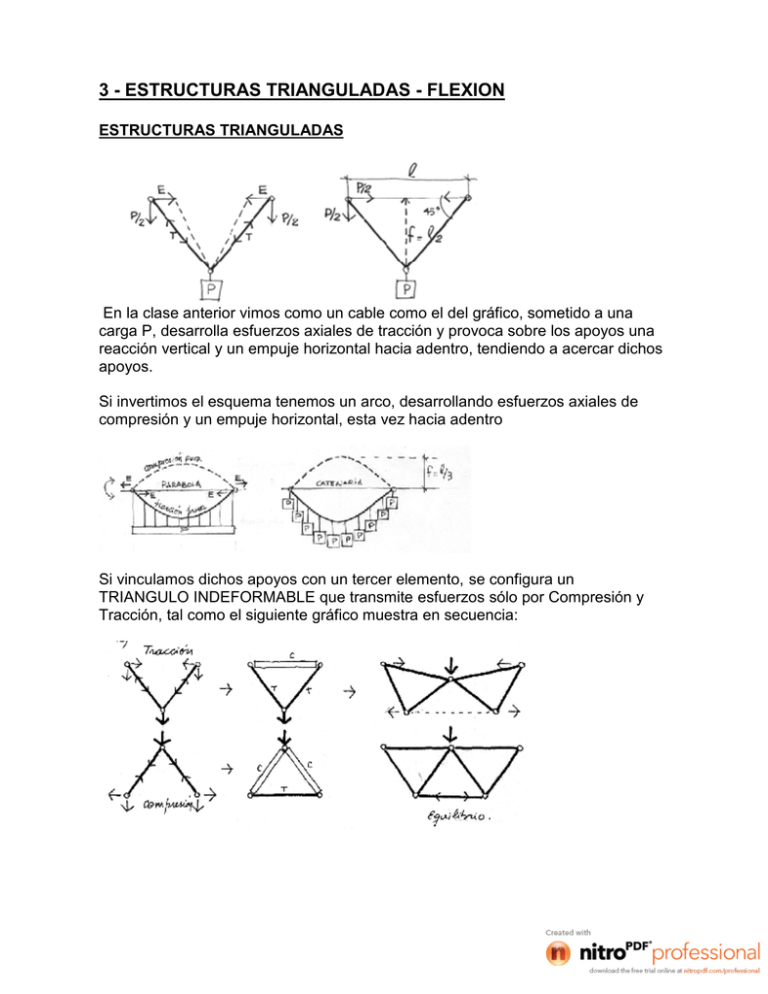
3 - ESTRUCTURAS TRIANGULADAS - FLEXION ESTRUCTURAS TRIANGULADAS En la clase anterior vimos como un cable como el del gráfico, sometido a una carga P, desarrolla esfuerzos axiales de tracción y provoca sobre los apoyos una reacción vertical y un empuje horizontal hacia adentro, tendiendo a acercar dichos apoyos. Si invertimos el esquema tenemos un arco, desarrollando esfuerzos axiales de compresión y un empuje horizontal, esta vez hacia adentro Si vinculamos dichos apoyos con un tercer elemento, se configura un TRIANGULO INDEFORMABLE que transmite esfuerzos sólo por Compresión y Tracción, tal como el siguiente gráfico muestra en secuencia: Como se observa en la última figura, uniendo una serie de estos triángulos se pueden cubrir grandes luces con elementos de pequeña sección. Por su Esbeltez, los elementos comprimidos pueden pandear. Las uniones de estas barras deben ser teóricamente consideradas como ARTICULADAS (sin transmitir Momentos) aunque en la práctica desarrollan pequeñas tensiones de flexión y corte debido a la rigidez de sus uniones (cartelas) LA FLEXION En las clases anteriores hemos visto como a partir de contar solo con material de compresión (piedra, ladrillo, etc.) conducimos las cargas al suelo mediante “la forma” de la estructura”: EL ARCO Y SUS DERIVADOS. - (El sistema “Trilítico” del Partenón, en realidad respondía más a necesidades de tipo arquitectónico que Estructural, en su afán de relacionar el interior con el exterior) En estas estructuras, las cargas de son “axiales” (de compresión ó de tracción), es decir, se desarrollan en la dirección del eje de la estructura, lo cual siempre es más eficiente ya que involucra a todo el material. Desde un punto de vista más arquitectónico, estas estructuras ocupaban proporcionalmente un gran porcentaje de la obra total –tanto de material como de espacio- dotando al artefacto arquitectónico de una escala importante, que trascendía la escala individual. Pero paralelamente se ha venido desarrollando desde siempre otra forma de conducir cargas al suelo: la “humilde” FLEXIÓN. ESTRUCTURALMENTE, la flexión es la transmisión en horizontal de cargas verticales con el fin de salvar una determinada distancia entre apoyos. En principio limitadas por la poca disponibilidad de materiales de tracción (Sólo maderas naturales de medidas limitadas), las estructuras de flexión son las habituales en la arquitectura anónima, popular. Este mecanismo no opera mediante la “Forma” sino aprovechando los “esfuerzos internos”que, combinando Tracción con Compresión. se oponen a la Deformación. Es decir, depende de : - La RESISTENCIA molecular del material ante los esfuerzos de Tracción y Compresión La RIGIDEZ aportada por Las dimensiones y forma de la sección No confundamos “Resistencia” con “Rigidez”: - La RESISTENCIA se opone al “ESFUERZO” (acortamiento, alargamiento) La RIGIDEZ se opone a la “DEFORMACIÓN” La rigidez flexional de la pieza dependerá mucho más de la “altura” que de la cantidad de materia, ya que aumenta al cuadrado de la distancia entre la fibra más alejada y el eje neutro. Se comprende así la importancia de la sección para la utilización racional del material. Por lo tanto, una pieza capaz de trabajar a la Flexión tiene que tener Resistencias de tracción muy similares, lo que explica el predominio de la madera para cumplir ese rol entre los materiales naturales, y del acero y el Hormigón Armado entre los artificiales. LA DEFORMACION Las estructuras de flexión se comprenden mejor si se analiza “LA DEFORMACIÓN” Todo elemento sometido a flexión se Deforma según una determinada curva o “Elástica de deformación”, de la cual se pueden deducir los tipos de esfuerzos requeridos a la pieza. - Analicemos “el Gusanito” que han construido: ¿Cuáles son las consecuencias de este análisis? - Máxima compresión y tracción en las fibras más alejadas del Eje Neutro Ahora, a la luz de esta constatación, analicemos una viga en voladizo sometida a una carga P - ¿Qué se ha producido en el interior de la pieza deformada? Se ha producido un “PAR INTERNO DE FUERZAS” que se opone a la deformación Par de Compresión y Tracción que será tanto mayor cuanto mayor sea su brazo de palanca, en función de la altura de la sección. EL CORTE Pero al mismo tiempo se pone en acción el ESFUERZO DE CORTE, mecanismo por el cual dos secciones infinitamente próximas tienden a deslizarse entre sí. El corte también podría considerarse como una combinación de tracción sobre una diagonal y de compresión sobre la otra. (Esta es la razón por la cual un material con baja resistencia a la tracción no puede ser resistente al corte.) LOS APOYOS El otro elemento que influye decisivamente en la forma de la Elástica de deformación es el Tipo de Apoyo de la pieza flexada Hay tres tipos de apoyos, según la cantidad de movimientos que restringen: TIPOS ESTRUCTURALES DE FLEXION A partir de estos conocimientos básicos es posible intentar intuir la deformación y analizar los esfuerzos a los que son sometidas las piezas estructurales. La correspondencia entre la “Elastica de deformación” y el “Diagrama de Momentos” permite comprender la relación que hay entre la Deformación” producida por las fuerzas exteriores, y las resistencias internas suscitadas en el material. Vamos a empezar viendo algunos ejemplos de piezas flexadas SOBRE UNA LÍNEA DE ACCIÓN, denominadas VIGAS. VIGA SIMPLEMENTE APOYADA VIGA EMPOTRADA VIGA CONTINUA VIGA EN VOLADIZO PORTICO