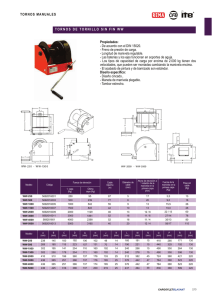
sistemas de fuerzas en 3 dimensiones - apoyos

CARTILLA DE ESTÁTICA
SISTEMAS DE FUERZAS EN EL ESPACIO - APOYOS - REACCIONES
1_ La estructura tubular soldad está unida al plano horizontal xy mediante una rótula en A y se
apoya en el anillo con holgura situado en B. El cable CD impide la rotación en torno a la recta AB
cuando se aplica la carga de 500 Kg y la estructura es estable en la posición presentada. Despréciese
el peso de la estructura frente a la carga aplicada y determínese la tensión T del cable, las reacciones
en el anillo y las componentes de la reacción en A.
El sistema es evidentemente tridimensional sin ejes ni
planos de simetría, por lo que habrá que analizar el
problema como uno de sistema general de fuerzas en
el espacio. Se realiza primero el diagrama de cuerpo
libre en el cual se ha representado la reacción del
anillo en función de sus dos componentes. Sumando
momentos respecto al eje AB puede eliminarse todas
las incógnitas menos T. La dirección de AB está
especificada por el vector unitario n = 1/5(3j + 4k). El
momento de T respecto AB es la proyección sobre AB
del momento respecto al punto A. Así pues , el
momento de T respecto AB está dado por r1*F*n. Las
expresiones vectoriales de T, F, r1 y r2 son:
La ecuación de momento se convierte ahora en:
Efectuando las operaciones se tiene:
Las componentes de T son:
Las incógnitas restantes se encuentran fácilmente por suma de momentos y suma de fuerzas, de la
siguiente manera:
Los signos negativos de las componentes de A indican que tienen sentidos contrarios a los elegidos
como positivos.
Para los alumnos:
a) ¿Cuál es la ventaja del empleo de notación vectorial en este problema?
b) ¿Cuántos grados de libertad tiene la estructura?
c) ¿Qué tipo de apoyo tiene? ¿Cuántos grados de libertad restringen cada uno?
d) Compara la respuesta de b y c y extraiga conclusiones.
e) ¿Si en A estuviera empotrado, cuál sería la respuesta b, c y d?
f) ¿Si no existiera el cable T, cuál sería la respuesta a b, c y d?
g) ¿Cuál es el punto de aplicación de la reacción que genera T? ¿Qué módulo, dirección y
sentido tiene?
h) Si el sentido positivo del eje “z” es descendente, y no ascendente como fué planteado,
¿existe alguna modificación? Explique y detalle escribiéndolas.
2_ Se aplica una fuerza de 50Kg a la manivela del torno en la forma que se indica. El cojinete A
soporta el empuje (fuerza en la dirección del eje del árbol) mientras que el cojinete B soporta
solamente la carga radial (carga normal al eje del árbol). Determinar el peso P que puede soportarse
y la fuerza radial total ejercida por cada cojinete sobre el árbol.
El
sistema
es
claramente
tridimensional sin ejes ni planos de
simetría, por lo que habrá que
analizar el problema como el de un
sistema
general
de
fuerzas
coplanarias. Para ilustrar este método
utilizaremos una solución con
escalares. El diagrama de cuerpo libre
correspondiente al árbol, manivela y
tambor
considerados
como
constituyentes de un cuerpo único, se
representa
mediante
sus
tres
proyecciones ortogonales.
La fuerza aplicada de 50Kg se resuelve según sus tres componentes y en cada uno de estos
esquemas pueden verse dos de estas componentes. Pueden verse los sentidos correctos de Ax y Bx si
se observa que la resultante de las dos fuerzas de 17.7 Kg ejerce un momento de sentido opuesto al
de las agujas del reloj respecto A. Los sentidos correctos de Ay y By no pueden determinarse hasta
haber obtenido los módulos de los momentos, por lo que podrán asignarse arbitrariamente. La
proyección xy de las fuerzas de los cojinetes se indica por una flecha ondulada por ser desconocida
su dirección. La adición de Az y P completan los diagramas de cuerpo libre. Obsérvese que las tres
secciones representan tres problemas bidimensionales relacionados por las correspondientes
componentes de las fuerzas.
De la proyección xy:
De la proyección xz
De la proyección yz da:
Las fuerzas radiales totales sobre los cojinetes resultan ser:
Para los alumnos:
a) Para el caso general de un sólido rígido en el espacio los grados de libertad son . . . . . . . . .
b) De ellos la mitad corresponden a . . . . . . . . . . . . . . . y la otra mitad a . . . . . . . . . . . . . . . . .
c) Los . . . . . . . . . . . . . . . . . . . . se miden respecto a los ejes . . . . . . . . . . . . . . . . . .
d) Las . . . . . . . . . . . . . . . . . . . . . . . se miden respecto a los . . . . . . . . . . . . . xy, xz, y . . . . . . .
e) Para el ejercicio anterior responda de acuerdo con los puntos a) y b)
f) Para el ejercicio anterior responda de acuerdo con los puntos c) y d)
g) ¿Qué sucede si la fuerza de 50 kg se aplica en la dirección z? Resuelva el planteo
matemáticamente, y analice los resultados.
h) ¿Qué sucede si al eje “x” lo cambiamos por el “z” y viceversa? ¿cambia algo? Si existieran
cambio escríbalos.
i) Si utilizáramos un sistema de ejes no ortogonales ¿el resultado diferiría? Escriba las ventajas
y desventajas de estos dos sistemas de ejes.