TURBINAS DE GAS
Anuncio
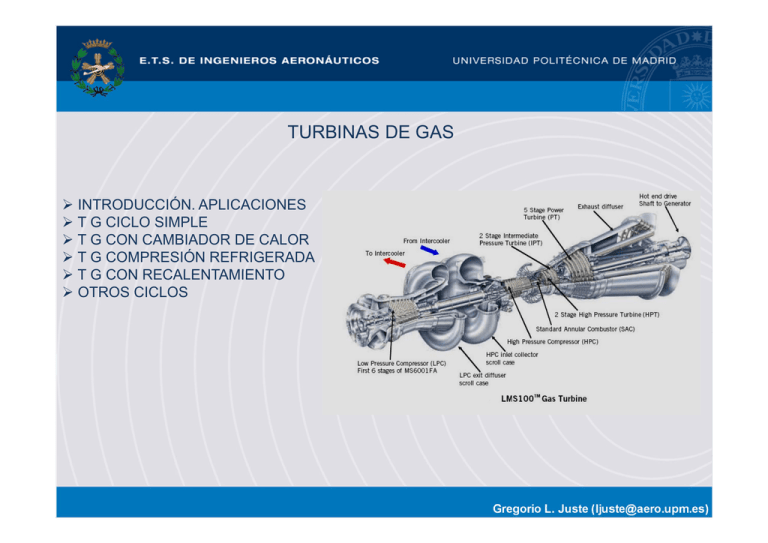
TURBINAS DE GAS ¾ INTRODUCCIÓN. APLICACIONES ¾ T G CICLO SIMPLE ¾ T G CON CAMBIADOR DE CALOR ¾ T G COMPRESIÓN REFRIGERADA ¾ T G CON RECALENTAMIENTO ¾ OTROS CICLOS INTROUDCCIÓN Ó La turbina de gas es una planta de potencia que produce gran cantidad de energía con poco peso y tamaño tamaño. Puede funcionar con una gran variedad de combustibles : gas natural, diesel, naphta, metano, gasóleos vaporizados, gases de biomasa. Gran crecimiento de utilización en los últimos años: mejora de materiales, refrigeración. g Incremento de temperaturas p y relaciones de compresión. p Aumento del rendimiento motor de 15% a valores del 45% El costo de operación de la planta de potencia y el coste de la energía depende de varios factores: Costo del combustible, eficiencias de funcionamiento, costos de mantenimiento y costo inicial. La elección del tipo de planta de potencia depende de esos factores y de su aplicación y localización. Aplicaciones A li i : G Generación ió d de energía í eléctrica lé t i ((grandes d y pequeñas ñ iinstalaciones) t l i ) ,propulsión marítima y terrestre Comparación de plantas de potencia Comparación de rendimientos de varias plantas de potencia Resumen: la turbina de gas una buena opción para generación de potencia Categorías de turbinas de gas Grandes turbinas de gas: unidades grandes de generación de potencia, 3 – 480 MW, configuración de ciclo simple y rendimientos 30-46% 30 46% π23 : 5:1 – 35:1 T4t : 1644– 1900 (futuros) Rendimiento : 50% Turbinas de gas aero-derivadas: Unidades de generación de potencia que tienen su origen g en motores de aviación,, en los cuales se ha q quitado el fan y se han añadido etapas de turbina. Potencias de 2.5 a 50 MW, rendimientos del 50% Turbinas de gas de tipo industrial: Potencias de 2.5 a 15 MW, utilizadas en petroquímicas para mover compresores compresores, rendimientos del orden del 30% Turbinas de gas pequeñas : potencias de 0.5 a 2.5 MW, suelen tener compresores centrífugos y turbinas radiales, radiales rendimientos bajos 15 al 25% Inciso : APU Micro-turbinas : potencias de 20 a 350 kw MEMS- Micro-turbinas APLICACIONES Turbinas de gas ⎧ ⎧ciclo simple ⎪ ⎪ ⎪ ⎪ ⎪ ⎪cambiador de calor ⎪ ⎪ ⎪ ⎪ ⎪ ⎪compresión ió refrigerada fi d ⎪ ⎪ ⎪Ciclo abierto ⎨ ⎪ ⎪combustión escalonada (reheat ) ⎪ ⎪ ⎪ ⎪ Clasificación ⎨ ⎪ciclos combinados ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩cogeneración ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩Ciclo cerrado Mono-ejes, turbina libre, biejes Análisis de la turbina de gas de ciclo simple Criterio de diseño : maximizar el comportamiento motor Wu = Wt − Wc V0 0 T2t = T0 ; P2t = P0 ηM = Wu cL CE = c Wu Gt = Gc ; cP constante Vs 0 ⇒ P5t = P5 = P0 , o se define d f ell rendimiento d totall estático á ⎧⎪ (T4t − T5t ) − cP (T3t − T2t ) = cP ⎨T4t ⎪⎩ teniendo en cuenta W τ u = u = cP G T5' ⎛ P0 ⎞ =⎜ ⎟ T4t ⎝ P4t ⎠ γ −1 γ γ −1 γ ⎛P ⎞ =⎜ 0 ⎟ ⎝ P3t ⎠ γ −1 γ ⎛ P3t ⎞ ⎜ ⎟ ⎝ P4t ⎠ γ −1 γ T3't ⎛ P3t ⎞ =⎜ ⎟ T0 ⎝ P0 ⎠ ⎧ ⎫ ⎛ ⎞ γ −1 ⎞⎪ 1 ⎪ ⎜ ⎟ T0 ⎛ γ τ u = cP ⎨T4tη45 ⎜1 − γ −1 γ −1 ⎟ − ⎜⎜ π 23 − 1⎟⎟ ⎬ η ⎪ ⎠⎪ ⎜ π γ π γ ⎟ 23 ⎝ 23 34 ⎠ ⎝ ⎩ ⎭ ⎛ T5't ⎜1 − ⎝ T4t ⎞ ⎞ ⎫⎪ T0 ⎛ T3't − 1⎟ ⎬ ⎟η45 − ⎜ η T 23 ⎝ 0 ⎠ ⎠ ⎪⎭ 1 1 ⎧ ⎫ 1 − α ⎪⎪ π 23 π 34α T0 α ⎪⎪ ⎛ 1 ⎞ τ u = cP ⎨T4tη45 − π 23 ⎬ ⎜1 − α ⎟ 1 η23 ⎪ ⎪ ⎝ π 23 ⎠ 1− α π 23 ⎪⎩ ⎪⎭ donde α = ⎡ ⎤ ⎫⎪ cP ⎧⎪ 1 α fL = (T4t − T3t ) = ⎨T4t − T0 ⎢1 + π 23 − 1) ⎥ ⎬ ( ηq ηq ⎩⎪ ⎣ η23 ⎦ ⎭⎪ cP 1− T4tη 45 1 1 α α π 23 π 34 1− 1 − T0 η23 α π 23 ⎛ 1 ⎞ ηM = ⎜ 1 − α ⎟η q ⎡ ⎤ ⎝ π 23 ⎠ 1 α T4t − T0 ⎢1 + π 23 − 1) ⎥ ( ⎣ η 23 ⎦ α π 23 γ −1 γ ciclo ideal ηij =1 η M =1 − i 1 γ −1 γ π 23 α suponiendo π 34 1 ⎧ τ u = cP ⎨T4tη45 − ⎩ ηM = T0 ⎫⎛ η23 T4tη45 − α π 23 ⎬ ⎜1 − T0 ⎭⎝ α π 23 1 ⎞ α ⎟ π 23 ⎠ ⎛ 1 ⎞ η 1 − ⎜ α ⎟ q π ⎡ ⎤ 1 α 23 ⎠ T4t − T0 ⎢1 + π 23 − 1) ⎥ ⎝ ( ⎣ η 23 ⎦ η23 Rendimiento motor y trabajo útil función de relación de compresión y T máxima ciclo, turbina ciclo simple p Consumo específico función potencia específica , turbina ciclo simple CE ∝ 1 ηM Interesan T4t altas : consumo específico disminuye y la potencia específica aumenta : alabes de turbina ceramicos El mínimo consumo específico se obtiene con relaciones de compresión más altas que el máximo de potencia específica La línea de máximos aproximadamente coincide con la línea en la que se cumple T3t = T5t (en ciclo ideal coincide) a la izquierda de esa línea T5t>T3t Potencia específica máxima : tamaño y peso Consumo específico mínimo : economía Turbina de gas con cambiador de calor 35 6 Turbinas optimizadas para potencia específica máxima máxima, el consumo específico es mayor que el mínimo, en esas condiciones, si T5t > T3t se puede utilizar un cambiador de calor para reducir el consumo específico Cambiadores de calor : flujos opuestos opuestos, cruzados cruzados, regenerativos regenerativos, etc etc. Definición rendimiento del cambiador de calor: Calor liberado por los gases de la turbina : Qt = Gt cP (T5t – T6t) Calor recibido p por los g gases del compresor p Qc = Gc cP((T35t – T3t) Suponiendo Gt = Gc y cp constante T5t – T6t = T35t – T3t T35t y T6t son incógnitas Valor máximo p posible de T35t : cuando el aire a la salida del compresor p alcanza la temperatura p de los gases de salida de la turbina Medida de la eficiencia del cambiador de calor : la relación del calor recibido al máximo posible que se puede recibir ηcc = T35t − T3t T5t − T3t τ u = cP (T4t − T5t ) − cP (T3t − T2t ) ηq Lc = GcP (T4t − T35t ) η MR = sesupone c << G Pu Gτ u cP (T4t − T5t ) − cP (T3t − T2t ) 1 = = ηq = cL cL c p (T4t − T35t ) LCE Utilizando la expresión del rendimiento del cambiador de calor T35t = T3t +ηcc (T5t − T3t ) η MR = cP (T4t − T5t ) − cP (T3t − T2t ) cP ⎡⎣T4t − T3t − ηcc (T5t − T3t ) ⎦⎤ ηq = 1 LCE Suponiendo cP iguales T4t − T3t ) − (T5t − T2t ) − ηcc (T5t − T3t ) +ηcc (T5t − T3t ) ( η MR = = T4t − T3t − ηcc (T5t − T3t ) T5t − T2t − ηcc (T5t − T3t ) = 1− T4t − T3t − ηcc (T5t − T3t ) ηMR (T5t - T3t ) Caso de rendimiento cambiador de calor = 1 η MR =1 − T3t − T2t T4t − T5t Suponiendo ciclo ideal V0 0 ⇒ T2t = T0 ; Vs 0 ⇒ P5t P0 T4t T3t = T5t T2t T3t η MR i −1 T3t − T2t T2t T2t T2t =1 − =1 − = =1 − T4t − T5t T5t T4t −1 T5t T5t η MR = 1 − i T2t T5t En el caso ηcc = 0 ηM =1 − i T2t T3t η MR + 1 T3t = η M + 1 T5t i i Limite de utilización : cuando T5t = T3t La potencia específica es ligeramente menor que en el ciclo por las perdidas de presión de remanso en el cambiador de calor Turbina de gas con recalentamiento o combustión escalonada: Suponemos π23 y T4t fijos j Objetivo: maximizar el trabajo total ⎡⎣(T4t − T45t ) − (T46t − T5t ) ⎤⎦ máximo τt cP = T4t − T45t + T46t − T5t ⎛ T ⎞ ⎛ T ⎞ = T4t ⎜1 − 45t ⎟ + T46t ⎜1 − 5t ⎟ ⎝ T4t ⎠ ⎝ T46t ⎠ γ −1 γ −1 ⎡ ⎤ ⎡ ⎤ γ γ ⎛ ⎞ ⎛ ⎞ P P = T4t η445 ⎢1 − ⎜ 45t ⎟ ⎥ + T46tη465 ⎢1 − ⎜ 0 ⎟ ⎥ ⎢ ⎝ P4t ⎠ ⎥ ⎢ ⎝ P45t ⎠ ⎥ ⎣⎢ ⎦⎥ ⎣⎢ ⎦⎥ Suponemos que no hay perdidas de presión de remanso P45t = P46t y T4t = T46t La única incógnita es P45t ⎛τ ⎞ γ −1 d⎜ t ⎟ γ −1 1− 2γ 1 γ − c ⎛ ⎞ γ − 1 γ − 1 1 ⎝ P ⎠ γ =η465T46t P0 γ P45tγ − T4t η445 P ⎜ ⎟ 45t = 0 dP45t γ γ ⎝ P4t ⎠ T46t ( P0 P4t ) γ −1 γ ⎛ γ −1 ⎞ 2⎜ ⎟ ⎝ γ ⎠ 45t η465 = T4t P γ ⎛ T46t η 465 ⎞ γ −1 P = ⎜ ⎟ P0 P4t ⎝ T4tη 445 ⎠ * 45t Si T46t = T4t y η 445 = η 465 P45* t = P0 P4t η445 η Mreheat = =1 − (T4t − T45t ) + (T46t − T5t ) − (T3t − T0 ) = (T4t − T3t ) + (T46t − T45t ) T5t − T0 (T4t − T3t ) + (T46t − T45t ) Turbinas de gas con compresión refrigerada Comparación de la compresión isoterma y compresión adiabática τ is = RT1 ln P2 P1 γ −1 ⎡ ⎤ γ ⎛ ⎞ P τ a = cP T1 ⎢⎜ 2 ⎟ −1⎥ ⎢⎝ P1 ⎠ ⎥ ⎢⎣ ⎥⎦ El trabajo requerido en una compresión isoterma es menor que una compresión adiabática. Una forma de aproximarse p a la compresión p isoterma es la compresión p refrigerada g Suponiendo p Pat = Pbt, el valor óptimo p Pat* = P2t P3t Comparación de ciclos Turbinas de gas con cambiador, refrigeración y combustión escalonada Ciclos combinados y cogeneración CONCLUSIONES Fabricantes de turbinas de gas Rangos dem potencias W - MW ¿PREGUNTAS? APLICACIONES Plantas de potencia y generación electrica Transporte terrestre Transporte marítimo


