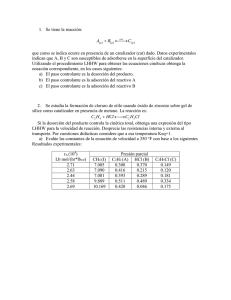
Tema: Termodinámica de superficie B. Quintero/ M.C. Cabeza 1
Anuncio

Tema: Termodinámica de superficie B. Quintero/ M.C. Cabeza Isoterma B.E.T. Hay procesos de adsorción que se producen gracias a la formación de enlaces débiles, básicamente enlaces por fuerzas de van der Waals. Este tipo de mecanismo que origina la adsorción sobre la superficie del sólido se conoce con el nombre de Fisisorción. En un proceso de fisisorción la cantidad de gas adsorbido aumenta al aumentar P sin que el volumen parezca que alcance un valor asintótico (ver figura). Esto significa que se produce una adsorción en multicapas. La isoterma B.E.T. (acrónimo de Brunauer, Emmett y Teller) puede ser utilizada para analizar este tipo de sistemas. La deducción de la expresión matemática de la isoterma B.E.T. requiere considerar dos diferencias fundamentales en relación con el modelo de Langmuir, concretamente que la superficie del sólido no es uniforme y que el gas se puede adsorber en varias capas Igual que en el modelo de Langmuir la superficie del sólido presenta diferentes sitios en los que pueden quedar retenidas las moléculas del gas, pero ahora se pueden diferenciar considerando que en el equilibrio el número de sitios vacíos es No. Por otro lado, el número de sitios con una molécula se designa como N1, los que retienen dos moléculas, N2 y así sucesivamente hasta considerar que hay un número i de sitios en los que se adsorbe un número Ni de moléculas de gas También cono en el modelo de Langmuir aquí se considera que el gas adsorbido está en equilibrio con el gas libre, distinguiéndose dos tipos de equilibrio Equilibrio en la primera capa a S A g SA (adsorción de la primera capa ) k k d en este equilibrio el sustrato S reacciona con una molécula del gas A(g) de modo que la molécula queda unida a la superficie, SA. Se considera, además, que la constante de velocidad del proceso de adsorción es ka, mientras que el proceso de desorción tiene una constante de velocidad kd. En lo que se refiere a los equilibrios que se establecen en las otras capas retenidas sobre el sólido los equilibrios se expresan del siguiente modo ' ka SA (adsorción de cualquier capa distinta a la primera) SAi 1 A g ' kd 1 Tema: Termodinámica de superficie B. Quintero/ M.C. Cabeza Para estos equilibrios el proceso de adsorción es similar al de la primera capa con la diferencia que ahora la constante de velocidad de adsorción es ka’ mientras que la de desorción es kd’. Estas constantes se diferencian de las definidas para la primera capa porque, en cualquier capa diferente de la primera, el proceso de adsorción tiene lugar entre una molécula A de gas libre y otra molécula A ya retenida, mientras que en la primera capa la situación es diferente ya que la adsorción tiene lugar entre una molécula A de gas libre y la superficie del sólido Admitiendo que se igualan las velocidades de adsorción y desorción se podrán establecer las siguientes ecuaciones Para la primera capa kd N1 k a PN o Para el resto de las capas kd' N 2 ka' PN1 kd' N 3 ka' PN 2 kd' N i k a' PN i 1 Se puede expresar el número de sitios con i capas en función del número de sitios vacíos, No. Para ello se puede suponer que se ha retenido hasta un máximo de tres capas de modo que, aplicando las ecuaciones anteriores al caso de la tercera capa ka' N k k a PN 2 N 3 ' PN 2 kd de forma similar se puede deducir que el número de sitios con dos capas de moléculas retenidas queda expresado como ' 3 d ' N2 ka' PN1 kd' y sustituyendo en la anterior ecuación se tendrá 2 k ' N 3 'a P 2 N1 kd siendo k N1 a PN o kd 2 k k ' N 3 a a' P 3 N o kd k d La ecuación final puede generalizarse a un sistema con i capas i 1 k k ' N i a a' kd k d Pi No 2 Tema: Termodinámica de superficie B. Quintero/ M.C. Cabeza Si ahora se admite que los cocientes de las constantes cinéticas son diferentes pero que están evidentemente relacionados porque implican al mismo adsorbato, se podrá escribir que ka' ka ' X ; X kd kd De manera que sustituyendo en la expresión general, el número de sitios con i capas queda expresado como N i X X ( i 1 ) P i N o i N i XP N o Teniendo en cuenta que el volumen total de gas adsorbido (V) es proporcional al número de moléculas adsorbidas i V N1 2 N 2 3 N 3 ... iN i i XP N o N o i XP i i i i y, admitiendo que el desarrollo de la sumatoria se puede aproximar del siguiente modo XP i i XP 1 XP 2 i de donde se obtiene V N o XP 1 XP 2 Por otra parte, el volumen de una monocapa (Vm) será proporcional al número de sitios en la superficie del sólido, o sea Vm N o N1 N 2 N 3 N o N i i y sustituyendo la expresión matemática deducida para Ni i i Vm N o XP N o N o N o XP i i en este caso la sumatoria equivale a XP i i XP 1 XP de modo que Vm N o N o XP 1 XP Así que N o XP 2 1 XP V XP N N XP N XP Vm 1 XP 1 XP XP o o o 1 XP 3 Tema: Termodinámica de superficie B. Quintero/ M.C. Cabeza Cuando se considera un conjunto de capas adsorbidas sobre el sólido, se puede aceptar que una capa intermedia está en las mismas condiciones que una molécula en el seno de una fase condensada (ver figura) Desde este punto de vista la adsorción sobre la capa más superficial podría ser representada por el siguiente equilibrio ' ka A g A fase condensada k' d Ya es conocido (I.N. Levine 5ª Edición, página 398) que en los equilibrios químicos en sistemas heterogéneos donde intervienen gases, la constante de equilibrio viene dada por la presión de los gases K k a' 1 X * ' kd P Así la ecuación anteriormente deducida se puede transformar para dar V XP Vm 1 XP 1 XP XP y reorganizando los términos se tiene P P* V Vm 1 P P* 1 P P* P P * Expresión conocida como isoterma B.E.T. Referencias. I.N. Levine “Fisicoquímica”. 5ª Edición. Vol. 1. Mc Graw-Hill/Interamericana de España S.A.U. 2004 . pp 486-488. P. W. Atkins “Fiscoquímica”. 2ª Edición. Addison-Wesley Iberoamericana S.A.. Wilmington. Delaware, USA. 1987. pp 896-902. P.W. Atkins “Química Física”. 6ª Edición. Ediciones Omega. Barcelona .1999. pp 862866. P.W. Atkins, J. de Paula “Química Física”. 8ª Edición. Ed. Médica Panamericana. Buenos Aires, Argentina. 2008. pp 917-921 4