BOLETÍN DE PROBLEMAS SISTEMAS TRIFÁSICOS EQUILIBRADOS

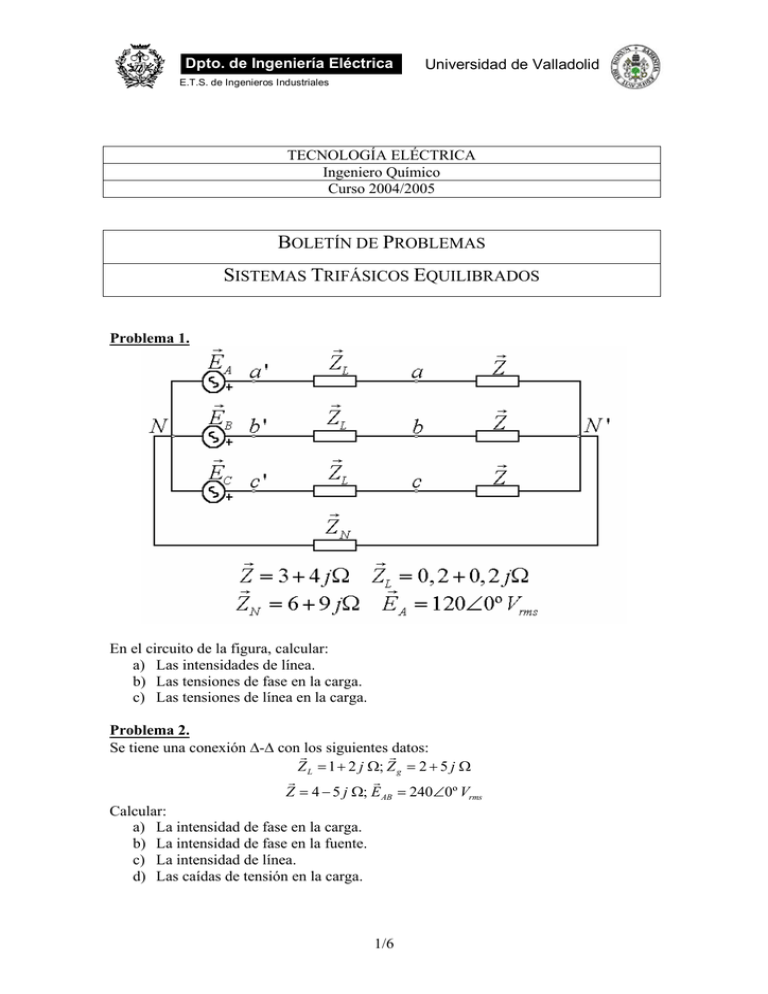
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
TECNOLOGÍA ELÉCTRICA
Ingeniero Químico
Curso 2004/2005
BOLETÍN DE PROBLEMAS
SISTEMAS TRIFÁSICOS EQUILIBRADOS
Problema 1.
En el circuito de la figura, calcular:
a) Las intensidades de línea.
b) Las tensiones de fase en la carga.
c) Las tensiones de línea en la carga.
Problema 2.
Se tiene una conexión ∆-∆ con Glos siguientes Gdatos:
Z L = 1 + 2 j Ω; Z g = 2 + 5 j Ω
G
G
Z = 4 − 5 j Ω; E AB = 240∠0º Vrms
Calcular:
a) La intensidad de fase en la carga.
b) La intensidad de fase en la fuente.
c) La intensidad de línea.
d) Las caídas de tensión en la carga.
1/6
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
Problema 3.
Se tiene una conexión ∆-∆ con Glos siguientes Gdatos:
Z L = 1 + 2 j Ω; Z g = 2 + 5 j Ω
G
G
Z = 4 − 5 j Ω; E AB = 240∠0º Vrms
Pasando a la configuración estrella-estrella equivalente, calcular:
e) La intensidad de fase en la carga.
f) La intensidad de fase en la fuente.
g) La intensidad de línea.
h) Las caídas de tensión en las cargas.
Problema 4.
Una carga trifásica con configuración en estrella y otra en triángulo están conectadas en
paralelo según muestra la figura.
La tensión de línea en el generador es de 208Vrms. Calcular:
a) Las tensiones de fase en las cargas.
b) Las tensiones de línea en las cargas.
Problema 5.
La carga trifásica de la figura se alimenta desde un sistema trifásico de tensiones
G
G
G
G
equilibrado de 380 V. Sabiendo que Z1 = Z 2 = Z 3 = 10∠36,87º Ω , y tomando U RN
como origen de fases, obtener los favores de tensión e intensidad de fase y de línea para
los dos casos siguientes:
1. Si el sistema de tensiones aplicado es de secuencia directa.
2. Si el sistema de tensiones aplicado es de secuencia inversa.
2/6
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
Problema 6.
La carga trifásica de la figura se alimenta desde un sistema trifásico de tensiones
G
G
G
G
equilibrado de 380 V. Sabiendo que Z1 = Z 2 = Z 3 = 10∠36,87º Ω , y tomando U RS
como origen de fases, obtener los favores de tensión e intensidad de fase y de línea para
los dos casos siguientes:
1. Si el sistema de tensiones aplicado es de secuencia directa.
2. Si el sistema de tensiones aplicado es de secuencia inversa.
Problema 7.
Un generador en estrella trabaja a 50 Hz y cede una potencia de 21,2 kW. La carga
pasiva consume 20 kW con f.d.p. 0,8 inductivo. La impedancia por fase de la línea es
1+j Ω. Calcular:
a) La intensidad, la tensión y la impedancia de la carga.
b) La batería de condensadores que se conectará en paralelo con la carga para que
el factor de potencia sea 0,9.
c) La nueva intensidad de línea, una vez instalada la batería de condensadores
calculada en el apartado anterior.
Problema 8.
En la línea trifásica equilibrada de la figura, de 380 Vrms de línea y 50 Hz, están
conectados tres receptores.
3/6
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
Calcular:
a) Intensidad consumida por cada uno de los receptores e intensidad total de línea.
b) Potencia aparente proporcionada por la línea.
c) Batería de condensadores si se quiere mejorar el factor de potencia hasta 1.
Problema 9.
Con un grupo generador trifásico de tensión eficaz 380 V se desea alimentar una carga
formada por:
‰ 3 motores trifásicos exactamente iguales de las siguientes características: 75 CV,
380 V de tensión nominal de alimentación, y factor de potencia 0,8 inductivo.
‰ Una carga resistiva formada por 150 resistencias de 100 W cada una, conectadas
a la red trifásica de una forma totalmente simétrica bajo una tensión de 380 Vrms.
La conexión del generador a la carga se realiza mediante una línea trifásica aérea a 380
Vrms que presenta una impedancia por fase de 0,01+0,1j Ω. Se pide:
a) Trazar un esquema del sistema trifásico que se quiere realizar conectando
correctamente todos los elementos.
b) Calcular la potencia consumida por la línea y determinar la potencia necesaria
que debe suministrar el generador.
c) Calcular la batería de condensadores conectada en triángulo necesaria para
aumentar el factor de potencia de la carga a 0,95.
d) Una vez instalada la batería de condensadores determinada en el apartado
anterior, volver a realizar los cálculos del apartado b.
4/6
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
Problema 10.
En la figura, la caída de tensión entre los nodos a y n vale 120∠0º Vrms . Hallar la lectura
de cada vatímetro y la potencia total.
Problema 11.
En el circuito de la figura, las tensiones son equilibradas y de secuencia directa, y la
tensión de línea vale 1000 Vrms. Sabiendo que la carga es puramente inductiva y que la
lectura del vatímetro es 1000 W, calcular:
a) Corriente de línea.
b) Valor de la impedancia por fase de la carga, si ésta está conectada en triángulo.
5/6
Dpto. de Ingeniería Eléctrica
Universidad de Valladolid
E.T.S. de Ingenieros Industriales
Problema 12.
Determinar las indicaciones de los vatímetros sabiendo que la carga consume 24 kW
con un factor de potencia 0,8 inductivo. El sistema es equilibrado y de secuencia
directa.
Problema 13.
El circuito trifásico de la figura se encuentra alimentado por un sistema trifásico de
tensiones equilibrado y de secuencia directa de 400 V. Sabiendo que:
G
G
G
• Z1 = Z 2 = Z 3 = 10 + j 20 Ω ;
G
G
G
• Z 4 = Z 5 = Z 6 = 5 − j 30 Ω ;
G
y tomando U RS como referencia de fases, calcular las intensidades de línea que
consumen las dos cargas, y las corrientes de fase en cada carga.
6/6