GRUPO B Se deben incluir los pasos detallados, así como la

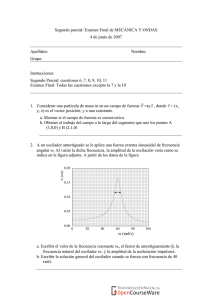
 GRUPO B Se deben incluir los pasos detallados, así como la realización de dibujos, diagramas y esquemas, y siempre que sea posible, las magnitudes vectoriales 1. Dos planetas, A y B, tienen el mismo radio. La intensidad del campo gravitatorio en la superficie del planeta A es tres veces superior a la intensidad del campo gravitatorio en la superficie del planeta B. Calcule: a) La relación entre las densidades de los dos planetas. b) La velocidad de escape desde la superficie del planeta B si se sabe que la velocidad de escape desde la superficie del planeta A es de 2 km/s 2. Una carga de +10 nC se distribuye homogéneamente en la región que delimitan dos esferas concéntricas de radios r1= 2 cm y r2= 4 cm. Utilizando el teorema de Gauss, calcule: a) El modulo del campo eléctrico en un punto situado a 6 cm del centro de las esferas. b) El modulo del campo eléctrico en un punto situado a 1 cm del centro de las esferas. Dato: Permitividad electrica del vacio ε0 = 8,85×10‐12 C2 N‐1m‐2 3. En una región del espacio hay un campo eléctrico E = 4×103 j NC−1 y otro magnético B = −0.5 i T. Si un protón penetra en esa región con una velocidad perpendicular al campo magnético: a) ¿Cuál debe ser la velocidad del protón para que al atravesar esa región no se desvíe? Si se cancela el campo eléctrico y se mantiene el campo magnético: b) Con la velocidad calculada en el apartado a) ¿qué tipo de trayectoria describe? ¿Cuál es el radio de la trayectoria? c) Determine el trabajo realizado por la fuerza que soporta el protón y la energía cinética con la que el protón describe esa trayectoria. Datos: Masa del protón = 1,67×10‐27 kg ; Valor absoluto de la carga del electrón, e = 1,60×10‐19 C 4. Una espira cuadrada de 2 cm de lado y 1,5 Ω de resistencia está inmersa en un campo magnético uniforme B = 0,03 T dirigido según el sentido positivo del eje X. La espira forma un ángulo α variable con el plano YZ como se muestra en la figura. a) Si se hace girar la espira alrededor del eje Y con una frecuencia de rotación de 60 Hz siendo ϕ0 = π/2 en el instante t=0, obtener la expresión de la fuerza electromotriz inducida en la espira en función del tiempo. b) Hallar la f.e.m. máxima y la intensidad de la corriente. 5. La figura muestra un hilo conductor rectilíneo y una espira conductora. Por el hilo circula una corriente continua. Justifica si se inducirá corriente si: a) La espira se mueve hacia la derecha. 6. Un muelle cuya constante elástica es k = 0,2 N cm‐1 tiene uno de sus extremos fijos a una pared. El extremo libre del muelle se encuentra unido a un cuerpo de masa 300 g, el cual oscila sin rozamiento sobre una superficie horizontal, siendo su energía mecánica igual a 0,3 J. Calcule: a) La velocidad máxima del cuerpo. b) Si la longitud del muelle en reposo es 25 cm indique en qué posición, medida con respecto al extremo fijo del muelle, se alcanza dicha velocidad. c) La máxima aceleración experimentada por el cuerpo. 7. Una onda transversal que se propaga en una cuerda, coincidente con el eje X, tiene por expresión matemática: y (x , t)= 2 sen (7t ‐ 4x) , donde x e y están expresadas en metros y t en segundos. Determine: a) La velocidad de propagación de la onda y la velocidad máxima de vibración de cualquier punto de la cuerda. b) La diferencia de fase entre dos puntos separados  metros. ¿Qué significado físico tiene ese desfase?