(1) (2) 2° 3° (1) Rango inferior al fijado para el grado (2) Rango
Anuncio
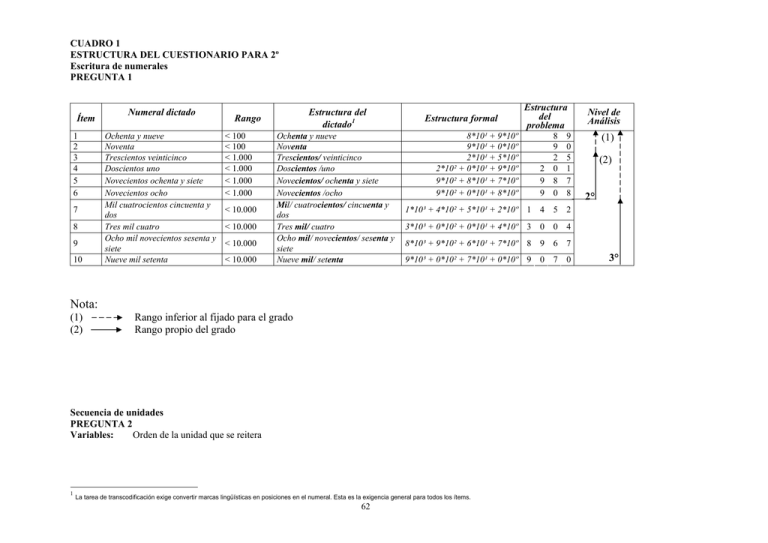
CUADRO 1
ESTRUCTURA DEL CUESTIONARIO PARA 2º
Escritura de numerales
PREGUNTA 1
Ítem
1
2
3
4
5
6
7
8
9
10
Numeral dictado
Ochenta y nueve
Noventa
Trescientos veinticinco
Doscientos uno
Novecientos ochenta y siete
Novecientos ocho
Mil cuatrocientos cincuenta y
dos
Tres mil cuatro
Ocho mil novecientos sesenta y
siete
Nueve mil setenta
Estructura del
dictado1
Rango
< 100
< 100
< 1.000
< 1.000
< 1.000
< 1.000
< 10.000
< 10.000
< 10.000
< 10.000
Ochenta y nueve
Noventa
Trescientos/ veinticinco
Doscientos /uno
Novecientos/ ochenta y siete
Novecientos /ocho
Mil/ cuatrocientos/ cincuenta y
dos
Tres mil/ cuatro
Ocho mil/ novecientos/ sesenta y
siete
Nueve mil/ setenta
Estructura formal
8*10¹ + 9*10º
9*10¹ + 0*10º
2*10¹ + 5*10º
2*10² + 0*10¹ + 9*10º
9*10² + 8*10¹ + 7*10º
9*10² + 0*10¹ + 8*10º
(1)
(2)
2°
8*10³ + 9*10² + 6*10¹ + 7*10º 8 9 6 7
9*10³ + 0*10² + 7*10¹ + 0*10º 9 0 7 0
Rango inferior al fijado para el grado
Rango propio del grado
La tarea de transcodificación exige convertir marcas lingüísticas en posiciones en el numeral. Esta es la exigencia general para todos los ítems.
62
9
0
5
1
7
8
3*10³ + 0*10² + 0*10¹ + 4*10º 3 0 0 4
Secuencia de unidades
PREGUNTA 2
Variables:
Orden de la unidad que se reitera
1
8
9
2
2 0
9 8
9 0
Nivel de
Análisis
1*10³ + 4*10² + 5*10¹ + 2*10º 1 4 5 2
Nota:
(1)
(2)
Estructura
del
problema
3°
Ítem
11
Pregunta
10, 20, 30, 40
_____________ 100
12
100, 200, 300
_____________ 10002
Rango
Estructura
formal
10 - 100
_____________ 290
Inferir diferencia: +/- 10
Aplicar + 10 para establecer secuencia
Escribir numerales correspondientes a
las decenas hasta 100
k + 100 i
k = 100 , i ∈{1,2,...,9}
•
•
•
k + 10 i
•
•
•
Inferir diferencia: +/- 100
Aplicar + 100 para establecer secuencia
Escribir numerales correspondientes a
las centenas hasta 1000
Inferir diferencias: +/- 10
Mantener el numeral anterior
Aplicar + 10 a numeral anterior para
Establecer secuencia
Escribir el siguiente, en el orden de las
decenas a partir de 230 hasta 290
k = 10
100 –1.000
Exigencias de la tarea
•
•
•
k + 10 i
13
210, 220, 230,
Estructura del
problema
, i ∈{1,2,...,9}
k = 200
, i ∈{1,2,...,9}
100 -1.000
•
Nivel de
análisis
2°
Descomposición multiplicativa
PREGUNTA 3
Ítem
14
Pregunta
Tienen una moneda de
100 pesos para
cambiar por monedas
de 10 ¿cuántas
monedas de 10 les
tienen que dar?
Rango
10 - 100
Estructura
formal
a* ?=c
Estructura del
problema
M1
M
1
Χ
M2
$
100
10
Exigencias de la tarea
•
•
•
•
•
Manejar valor de moneda de 100
Manejar valor de moneda de 10
Dividir 100 por o entre 10
Obtener resultado
Escribir resultados
Nivel de
análisis
2°
2
En la prueba, el ultimo numeral es 1.200. Sin embargo, se califica como correcta si la resuelve hasta 1.000 porque la raya donde los alumnos escribían los numerales no fue suficiente para escribir hasta el 1.200
debido al tamaño de los numerales de los niños.
63
Composición aditiva y multiplicativa de numerales
PREGUNTA 4
Variables: Rango numérico
Presentación gráfica
Ítem
15
16
17
Rango
Estructura
formal
Aquí hay $_____pesos
1 - 100
a *b=c
Aquí hay $_____pesos
1 - 10
a1 * b1 = c1
Pregunta
En total hay $______
pesos
10 - 100
c + c1 = d
Estructura del
problema
M2
$
10
Χ
M1
M
1
4
Estado
Estado
Estado
Exigencias de la tarea
•
•
•
Establecer numero de monedas: 4
Manejar valor de moneda: 10 pesos
Multiplicar número de moneda (4) por
el valor de moneda (10)
•
•
•
•
Contar número de monedas: 7
Manejar valor de moneda: 10 pesos
Obtener resultado
Escribir resultado: 7
•
Unir o componer aditivamente los
resultados parciales 40 y 7
Obtener resultado de unión o
composición
Escribir resultado: 47
•
•
Nivel de
análisis
2°
Composición aditiva y multiplicativa de numerales y aditiva de unidades
PREGUNTA 5
Variables: Rango numérico
Presentación gráfica
Ítem
Pregunta
Rango
Estructura
Estructura del
64
Exigencias de la tarea
Nivel de
formal
18
Aquí hay $_____pesos
1 - 100
problema
a *b=c
19
Aquí hay $_____pesos
1 - 10
a1 * b1 = c1
20
En total hay $____ pesos
10 - 100
c + c1 = d
M2
$
10
Χ
M1
M
1
9
Estado
21
22
Si les regalan un peso
¿Cuánto dinero
completan?________
¿Por cuál moneda
pueden cambiar el
dinero?
1 - 100
Estado
Estado
análisis
•
•
•
•
•
•
•
•
•
Contar número de monedas: 9
Manejar valor de moneda: 10
Multiplicar número de monedas (9) por
el valor de moneda (10)
Obtener resultado
Escribir resultado: 90
Contar número de monedas: 9
Manejar valor de moneda: 1
Obtener resultado
Escribir resultado: 9
•
•
•
Unir o componer aditivamente 90 y 9
Obtener resultado de la composición
Escribir 99
•
•
•
•
Agregar 1 a 99
Resolver algoritmo
Sumar 9 + 1 =10, en el orden de las
unidades
Escribir 0
Llevar 1 al orden de las decenas
Sumar 9 + 1 = 10, en el orden de las
decenas
Escribir 103
•
•
•
•
•
Manejar valor de moneda de 100
Manejar valor de moneda de 10
Dividir 100 por o entre 10
Obtener resultado
Escribir resultados
•
•
•
d+e=f
10 – 1.000
2°
No se analiza4
Composición aditiva de unidades
PREGUNTA 6
Variables: Rango numérico
Presentación verbal
Ítem
23
3
4
Pregunta
Rango
Estructura
formal
Tienen 90 pesos y les
regalan 10 pesos,
¿Cuánto dinero
completan?
10 - 100
d+e=f
Estructura del
problema
Exigencias de la tarea
•
•
•
En esta pregunta, el problema que el alumno enfrenta es obtener resultado y no el rango numérico de la tarea
Este ítem no se analiza porque es un problema de comparación y no de equivalencia. El ítem no mide lo que intenta medir
65
Agregar 10 a 90
Obtener resultado
Escribir resultado: 100
Nivel de
análisis
•
•
24
25
26
Tienen 190 pesos y les
regalan 10 pesos,
¿Cuánto dinero
completan?
10 - 1.000
Tienen 299 pesos y les
regalan 1 peso,
¿Cuánto dinero
completan?
1 - 1.000
Tienen 400 pesos y les
regalan 100 pesos,
¿Cuánto dinero
completan?
•
•
Agregar 10 a 190
Obtener resultado utilizando el
algoritmo
Sumar en las unidades 0+0=0
Escribir 0
Sumar en las decenas 9+1=10
Escribir 0 y llevar 1 al orden de las
centenas
Sumar en las centenas 1+1=2
Escribir 2
Agregar 1 a 299
Sumar en las unidades 9+1=10
Escribir 0 y llevar 1 al orden de las
decenas
Sumar en las decenas 9+1=10
Escribir 0 y llevar 1 al orden de las
centenas
Sumar en las centenas 1+2=3
Escribir 3
•
•
•
•
•
•
•
Agregar 100 a 400
Sumar en las unidades 0+0=0
Escribir 0
Sumar en las decenas 0+0=0
Escribir 0
Sumar 4+1=5 en las centenas
Escribir 5
•
•
•
•
•
•
•
•
•
•
•
100 -1.000
2°
Descomposición multiplicativa
PREGUNTA 7
Variables: Rango numérico
Valor del dinero que se cambia y número de monedas por las que se efectúa el cambio
Ítem
Pregunta
Rango
27
¿Cuántas monedas de
10 pesos necesitan
para tener 40 pesos?
10 - 100
28
¿Cuántas monedas de
1 peso necesitan para
tener 40 pesos?
1 – 100
29
¿Cuántas monedas de
100 pesos necesitan
para tener 300 pesos?
100 –1.000
Estructura
formal
a*?=c
Estructura del
problema
M2
$
100
10
M1
M
1
Χ
66
Exigencias de la tarea
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Manejar el valor de moneda de 10
Manejar 40 pesos
Dividir 40 por o entre 10
Obtener resultado
Escribir resultado
Manejar el valor de moneda de 1
Manejar 40 pesos
Dividir 40 por o entre 1
Obtener resultado
Escribir resultado
Manejar el valor de moneda de 100
Manejar 300 pesos
Dividir 300 por o entre 100
Obtener resultado
Escribir resultado
Nivel de
análisis
30
¿Cuántas monedas de
10 pesos necesitan
para tener 300 pesos?
10 - 1.000
31
¿Cuántas monedas de
1 peso necesitan para
tener 300 pesos?
1 - 1.000
•
•
•
•
•
•
•
•
•
•
67
Manejar el valor de moneda de 10
Manejar 300 pesos
Dividir 300 por o entre 10
Obtener resultado
Escribir resultado
Manejar el valor de moneda de 1
Manejar 300 pesos
Dividir 300 por o entre 1
Obtener resultado
Escribir resultado
2°
ESTRUCTURA DE CUESTIONARIOS PARA 3º y 4º y 5º
Escritura de numerales
PREGUNTA 1
Variables de la pregunta:
Ítem
1
2
3
4
5
6
7
8
9
10
11
12
13
Rango numérico
Numerales con y sin cero
Numeral dictado
Rango
Estructura del dictado5
Trescientos veinticinco
Doscientos uno
Novecientos ochenta y siete
Novecientos ocho
Mil cuatrocientos cincuenta y
dos
Tres mil cuatro
Ocho mil novecientos sesenta
y siete
Nueve mil setenta
Treinta y cuatro mil
doscientos cuarenta y tres
Veinte mil ciento tres
Noventa y siete mil quinientos
ochenta y seis
Ochenta y cinco mil siete
Quinientos cuarenta y tres
mil ciento cincuenta y dos
100 - 1.000
Trescientos / veinticinco
Doscientos / uno
Novecientos / ochenta y siete
Novecientos / ocho
Mi l/ cuatrocientos / cincuenta
y dos
Tres mil / cuatro
Ocho mil / novecientos /
sesenta y siete
Nueve mil / setenta
Treinta y cuatro mil /
doscientos cuarenta y tres
Veinte mil ciento / tres
Noventa y siete mil /
quinientos / ochenta y seis
Ochenta y cinco mil / siete
Quinientos cuarenta y tres
mil / ciento / cincuenta y dos
1.000 - 10.000
10.000 100.000
100.0001.000.000
14
Ciento cuatro mil dos
Ciento / cuatro mil / dos
15
Novecientos ochenta y siete
mil seiscientos cincuenta y
ocho
Novecientos / ochenta y siete
mil seiscientos / Cincuenta y
ocho
16
Ochocientos mil nueve
Ochocientos mil nueve
3*102 + 2*101 + 5*100
2*102 + 0*101 + 1*100
9*102 + 8*101 + 7*100
9*102 + 0*101 + 8*100
5
2
0
8
0
5
1
7
8
2
1
0
3 0 0 4
3
2
1
0
8 9 7 7
3
2
1
0
4
3
2
1
3*10 + 0*10 + 0*10 + 4*10
8*10 + 9*10 + 7*10 + 7*10
9*10 + 0*10 + 7*10 + 0*10
3*10 + 4*10 + 2*10 + 4*10 + 3*10
0
2*104 + 0*103 + 1*102 + 0*101 + 3*100
2
1
0
9 7 5 8 6
4
3
2
1
0
8 5 0 0 7
8*10 + 5*10 + 0*10 + 0*10 + 7*10
5*105 + 4*104 + 3*103 + 1*102 + 5*101 +
2*100
1*105 + 0*104 + 4*103 + 0*102 + 0*101 +
2*100
(2)
2 0 1 0 3
3
4°
5 4 3 1 5 2
1 0 4 0 0 2
9*105 + 8*104 + 7*103 + 6*102 + 5*101 +
8*100
9 8 7 6 5 8
8*105 + 0*104 + 0*103 + 0*102 + 0*101 +
9*100
8 0 0 0 0 9
La tarea de transcodificación exige convertir marcas lingüísticas en posiciones en el numeral. Esta es la exigencia general para todos los ítems.
(1)
9 0 7 0 3°
3 4 2 4 3
4
9*10 + 7*10 + 5*10 + 8*10 + 6*10
Nivel de
análisis
1 4 5 2
3
Rango inferior al fijado para el grado
Rango propio del grado
68
3
2
9
9
1*103 + 4*102 + 5*101 + 2*100
Nota:
(3)
(4)
Estructura
del
problema
Estructura formal
5°
Composición aditiva unidades
PREGUNTA 2
Variables de la pregunta:
Rango numérico
orden de la unidad que se adiciona
Ítem
17
Pregunta
999 + 1
Rango
1 – 1.000
Estructura
formal
Estructura del
problema
Exigencias de la tarea
•
•
•
•
•
a+b=?
•
•
18
9.990 + 10
1 – 10.000
•
•
•
•
•
a+b=?
•
•
•
•
19
99.900 + 100
1 – 100.000
•
•
•
•
•
•
•
a+b=?
•
•
•
•
69
Agregar 1 a 999
Sumar en las unidades 9+1=10,
Escribir 0 y llevar 1 al orden de las decenas
Sumar en las decenas 9+1=10
Escribir 0 y llevar 1 al orden de las centenas
Sumar en las centenas 9+1=10
Escribir 10
Agregar 10 a 9.990
Sumar en las unidades 0+0=0,
Escribir 0 en posición de las unidades
Sumar en las decenas 9+1=10
Escribir 0 y llevar 1 al orden de las centenas
Sumar en las centenas 9+1=10
Escribir 0 y llevar 1 al orden de las unidades
de mil
Sumar en las unidades de mil 9+1
Escribir 10
Agregar 100 a 99.900
Sumar en las unidades 0+0=0,
Escribir 0 en posición de las unidades
Sumar en las decenas 0+0=0,
Escribir 0 en posición de las decenas
Sumar en las centenas 9+1=10
Escribir 0 y llevar 1 al orden de las unidades
de mil
Sumar en las unidades de mil 9+1=10
Escribir 0 y llevar 1 al orden de las decenas
de mil
Sumar en las decenas de mil 9+1=10
Escribir 10
Nivel de
análisis
3°
4°
5°
Composición multiplicativa de unidades del sistema
PREGUNTA 3
Variables de la pregunta:
Ítem
20
21
Pregunta
Rango numérico
Rango
10 monedas de
100 pesos.
¿Cuánto dinero
tienen?
10 – 1.000
100 monedas de
100 pesos.
¿Cuánto dinero
tienen?
100 –
10.000
Estructura
formal
a*b = c
Estructura del
problema
M1
M
1
10
M2
$
100
Χ
Exigencias de la tarea
•
•
•
•
•
•
•
•
•
•
70
Manejar valor de moneda: 100
Manejar número de monedas: 10
Multiplicar valor de moneda (100)
por número de monedas (10)
Obtener resultado
Escribir resultado (1.000)
Manejar valor de moneda: 100
Manejar número de monedas: 100
Multiplicar valor de moneda (100)
por número de monedas (100)
Obtener resultado
Escribir resultado (10.000)
Nivel de
análisis
3° 4° y 5°
Composición multiplicativa y aditiva de numerales
PREGUNTA 4
Variable de la pregunta:
Formato de presentación verbal/gráfica
Ítem6
3°
4°
5°
22
Estructura formal
¿Cuánto dinero hay en
1 – 100
monedas de 10? $60
a *b=c
a1 * b1 = ?
a2 * b2 = ?
a3 * b3 = ?
¿Cuánto dinero hay en
1 – 10
monedas de 1? $___*7
a1 * b1 = ?
¿Cuánto dinero hay en
1 - 1.000
monedas de 1.000?
$___*
23
24
Rango
¿Cuánto dinero hay en
1 – 100
monedas de 100?
$___*
22
8
Pregunta
¿Cuánto dinero hay
entre todas las
monedas? $___
1.000 10.000
Estructura del
problema
M1
M
1
6
M2
$
10
Χ
•
Nivel de
análisis
Ejemplo
No ha sido analizado
•
•
•
a2 * b2 = ?
•
•
•
•
•
•
a3 * b3 = ?
c + c1+ c2+ c3 = d
Exigencias de la tarea
•
•
•
Estado
Estado
Estado
Estado
Estado
6
•
Establecer número de monedas: 5
Manejar valor de moneda: 100
Multiplicar número de monedas (5)
por valor de moneda (100)
Obtener resultado
Escribir resultado (500)
Colocar resultado en posición correcta
en relación con numerales precedentes
Establecer número de monedas: 6
Manejar valor de moneda: 1.000
Multiplicar número de monedas (6)
por valor de moneda (1.000)
Obtener resultado
Escribir resultado (6.000)
Colocar
Componer aditivamente valor inicial
dado y resultados parciales obtenidos
3°,4° y 5°
los ítems 22 y 23 para 3° y 4° se formulan en función del proceso de solución exigido por el ítem 24. Estos ítems no se incluyen en el cuestionario para 5° grado, se supone que en 5°, los alumnos deben manejar
el proceso que permite solucionar la pregunta. Solamente, si la pareja de alumnos logra realizar el proceso, su respuesta resulta correcta. La omisión de los ítems, cambia la numeración para el cuestionario de 5°
grado
7
Esta pregunta no evalúa el carácter multiplicativo del sistema y resulta tan fácil para los alumnos de estos grados que no se tiene en cuenta para el análisis.
8
En el formulario para los alumnos de 5º, ésta es la única pregunta que se les propone.
71
PREGUNTA 5
Variable de las preguntas 5 y 6:
Rango numérico
Formato de presentación verbal escrito
Ítem
3°
4°
5°
Pregunta
Rango
Juan tiene 10 monedas
de 1.000, 8 monedas
de 10 pesos y 3
monedas de 1 peso
25
26
27
28
23
24
25
26
¿Cuánto dinero tiene
Juan en monedas de
1.000 pesos?
¿Cuánto dinero tiene
Juan en monedas de
10 pesos?
¿Cuánto dinero tiene
Juan en monedas de 1
peso?
¿Cuánto dinero tiene
Juan?
Estructura formal
a*b=c
a1*b1= ?
a2*b2= ?
a3*b3= ?
10-10.000
Estructura del
problema
M1
M
1
10
M2
$
100
Χ
•
•
•
•
•
•
•
10 –100
1 –10
1–
10.000
a2*b2=?
•
•
•
•
•
•
•
•
a3*b3=?
C + c1+ c2+ c3 = d
Estado
Estado
Estado
•
Estado
Interpretar texto
No ha sido analizado
•
•
•
a1*b1=?
Nivel de
análisis
Exigencia
Establecer número de monedas: 10
Manejar valor de moneda: 1.000
Multiplicar número de monedas (10)
por valor de moneda (1.000)
Obtener resultado
Escribir resultado (10.000)
Colocar resultado en posición correcta
en relación con numerales precedentes
Establecer número de monedas: 8
Manejar valor de moneda: 10
Multiplicar número de monedas (8)
por valor de moneda (10)
Obtener resultado
Escribir resultado (80)
Colocar resultado en posición correcta
en relación con numerales precedentes
Establecer número de monedas: 3
Manejar valor de moneda: 1
Obtener resultado
Escribir resultado: 3
Colocar resultado en posición correcta
en relación con numerales precedentes
Componer aditivamente resultados
parciales obtenidos
3º
72
4º 5º
PREGUNTA 6
Ítem
3°
4°
5°
Pregunta
Rango
a*b=c
a1*b1=?
a2*b2=?
a3*b3=?
María tiene 10 billetes
de 10.000, 9 monedas
de 1.000 pesos y 7
monedas de 100 pesos
29
30
27
28
¿Cuánto dinero tiene
María en billetes de
10.000 pesos?
¿Cuánto dinero tiene
María en monedas de
1.000 pesos?
Estructura formal
Estructura del
problema
M1
M
1
10
M2
$
10.000
Χ
Exigencias de la tarea
•
•
•
•
•
•
•
10 –
10.000
•
•
•
•
•
•
31
29
¿Cuánto dinero tiene
María en monedas de
100 pesos?
10 - 1.000
32
30
¿Cuánto dinero tiene
María?
>100.000
•
•
•
c + c1+ c2+ c3 = d
Estado
Estado
Estado
Estado
Interpretar texto
No ha sido analizado
•
•
•
10 –
100.000
Nivel de
análisis
•
Establecer número de monedas: 10
Manejar valor de moneda: 10.000
Multiplicar número de monedas (10)
por valor de moneda (10.000)
Obtener resultado
Escribir resultado (100.000)
Colocar resultado en posición correcta
en relación con numerales precedentes
Establecer número de monedas: 9
Manejar valor de moneda: 1.000
Multiplicar número de monedas (9)
por valor de moneda (1.000)
Obtener resultado
Escribir resultado (9.000)
Colocar resultado en posición correcta
en relación con numerales precedentes
Establecer número de monedas: 7
Manejar valor de moneda: 100
Multiplicar número de monedas (7)
por valor de moneda (100)
Obtener resultado
Escribir resultado (700)
Colocar resultado en posición correcta
en relación con numerales precedentes 3°
Componer aditivamente
resultados parciales obtenidos
4° 5°
73
Descomposición de numerales
PREGUNTA 7
Variable de la pregunta:
Ítem
3° 5°
4°
Pregunta y
ejemplo
Así se escribe
925 así se
descompone:
900 + 20 + 5
33
31
3.083
Rango numérico
Rango
Estructura
formal
Estructura del problema
Ejemplo
m
10 –
1.000
1.000 10.000
n = ∑ k10 i
i =0
925 = 900 + 20 + 5
No ha sido analizado
k ∈ {0,1,2,..,9}
•
•
3.083 = 3.000 + 80 + 3
•
•
•
34
32
8.004
1.000 10.000
•
8.004 = 8.000 + 4
•
•
•
35
33
13.425
10.000 100.000
13.425 = 10.000 + 3.000 + 400 + 20 + 5
•
•
•
•
•
•
36
34
50.211
10.000 100.000
Nivel de
análisis
Exigencias de la tarea
50.211 = 50.000 +200 + 10 + 1
•
•
•
74
Comprender el numeral como producto de
composiciones aditivas sucesivas
Comprender que 3 en la posición de las
unidades de mil equivale a 3.000
Comprender que 8 en la posición de las
decenas equivale a 80
Utilizar 3 unidades como ultimo termino
Comprender el numeral como producto de
composiciones aditivas sucesivas
Comprender que 8 en la posición de las
unidades de mil equivale a 8.000
Utilizar 4 unidades como ultimo termino
Comprender el numeral como producto de
composiciones aditivas sucesivas
Comprender que 1 en la posición de las
unidades de diez mil equivale a 10.000
Comprender que 3 en la posición de las
unidades de mil equivale a 3.000
Comprender que 4 en la posición de las
centenas equivale a 400
Comprender que 2 en la posición de las
decenas equivale a 20
Utilizar 5 unidades como ultimo termino
Comprender el numeral como producto de
composiciones aditivas sucesivas
Comprender que 5 en la posición de las
unidades de diez mil equivale a 50.000
Comprender que 2 en la posición de las
centenas equivale a 200
Comprender que 1 en la posición de las
decenas equivale a 10
Utilizar 1 unidades como ultimo termino
3°
4° 5°
Descomposición multiplicativa
PREGUNTA 8
Variables de la pregunta:
Ítem
5°
3°
4°
37
38
Problema
Rango numérico
Unidades del Sistema de Notación en Base Diez (SNBD)
Rango
Estructura formal
35
Cambiar un billete de
1.000 pesos por
100 –
monedas de 100.
¿Cuántas monedas de 1.000
100 les tienen que dar?
a*?=c
36
Cambiar un billete de
10.000 pesos por
100 monedas de 100.
¿Cuántas monedas de 10.000
100 les tienen que dar?
a*?=c
Estructura del
problema
M2
$
1.000
100
M1
M
1
Χ
•
•
•
•
•
•
•
•
•
•
•
•
39
37
¿Cuántas monedas de
1.000 por 100.000
pesos?
1.000 –
100.000
a*?=c
40
38
Cuántas monedas de
100 por 100.000
pesos?
100 100.000
•
•
•
•
•
a*?=c
•
•
•
75
Nivel de
análisis
Exigencias de la tarea
Manejar valor del billete de 1.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 100 pesos
Dividir 1.000 entre 100
Obtener resultado
Escribir resultado
Manejar valor del billete de 10.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 100 pesos
Dividir 10.000 entre 100
Obtener resultado
Escribir resultado
Manejar el valor de 100.000
Manejar el valor de las monedas por las
cuales se deben cambiar: 1.000 pesos
Dividir 100.000 entre 1.000
Obtener resultad
Escribir resultado
Manejar el valor de 100.000
Manejar el valor de las monedas por las
cuales se deben cambiar: 100 pesos
Dividir 100.000 entre 100
Obtener resultado
Escribir resultado
3°
4° 5°
Descomposición multiplicativa
PREGUNTA 9
Variables de las preguntas 9 y 10:
Rango numérico
Unidades en un periodo dado
Ítem
3°
4°
5°
Problema
Rango
Cuántas monedas de 10
10 – 1.000
necesitan para tener 900?
41
39
Cuántas monedas de 100
100 - 1.000
necesitan para tener 900?
42
40
Cuántas monedas de 1
1 – 1.000
necesitan para tener 900?
PREGUNTA 10
Ítem
Problema
3°
5°
4°
9
Rango
Estructura formal
a*?=c
Estructura del problema9
M2
$
10
900
M1
M
1
Χ
Ejemplo
No se analiza
•
•
a*?=c
•
•
•
•
•
a*?=c
•
•
•
Estructura formal
Estructura del problema
M2
$
10
900
M1
M
1
Χ
•
•
43
41
44
42
Cuántas monedas de 100
necesitan para tener
3.000?
100 –
10.000
a*?=c
45
43
Cuántas monedas de 10
necesitan para tener
3.000?
10 –
10.000
•
•
•
•
•
a*?=c
46
44
Cuántas monedas de 1
necesitan para tener
3.000?
•
•
•
•
•
1 - 10.000
a*?=c
•
•
•
a*?=c
•
•
•
•
•
La estructura de multiplicación inversa se aplica para los demás ítems de descomposición multiplicativa de las preguntas 9 y 10
76
Manejar valor del dinero: 900
Manejar el valor de las monedas por
las cuales se debe cambiar: 100 pesos
Dividir 900 entre 100
Obtener resultado
Escribir resultado
Manejar valor del dinero : 900
Manejar el valor de las monedas
por las cuales se debe cambiar: 1 peso
Dividir 900 entre 1
Obtener resultado
Escribir resultado
3º, 4º y 5º
Nivel de
análisis
Exigencias de la tarea
Cuántas monedas de
1.000 necesitan para
tener 3.000?
1.000 –
10.000
Nivel de
análisis
Exigencias de la tarea
Manejar valor del dinero : 3.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 1.000 pesos
Dividir 3.000 entre 1.000
Obtener resultado
Escribir resultado
Manejar valor del dinero: 3.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 100 pesos
Dividir 3.000 entre 100
Obtener resultado
Escribir resultado
Manejar valor del dinero: 3.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 10 pesos
Dividir 3.000 entre 10
Obtener resultado
Escribir resultado
Manejar valor del dinero: 3.000
Manejar el valor de las monedas por
las cuales se debe cambiar: 1 peso
Dividir 3.000 entre 1
Obtener resultado
Escribir resultado
3º
4º y 5º
Secuencia de unidades
PREGUNTA 11
Variable de la pregunta:
Ítem
5°
3°
4°
47
48
Pregunta
Orden de la unidad que se itera
Rango
45
1.110, 1.120, 1.130,
_______ 1.190
1.000 10.000
46
3.130, 3.230, 3.330,
_______ 3.930
1.000 10.000
Estructura formal
k + 10 i
k = 1 . 110
, i∈{1,2,...,8}
Estructura del
problema
1100 + 10, 1120 + 10,
•
•
•
•
•
•
k + 100 i
k = 3 . 130
Exigencia
, i∈{1,2,...,8}
77
Inferir diferencia: +/- 10
Aplicar + 10 para establecer secuencia
Escribir numerales correspondientes a
las decenas hasta 1.190
Inferir diferencia: +/- 100
Aplicar + 100 para establecer secuencia
Escribir numerales correspondientes a
3º
las centenas hasta 3.930
Nivel de
análisis
4º y 5º
Cuadro 2. Criterios que permiten definir comprensión: Cuestionario 1
Componente
Rango y ejemplos para 2º
Criterio de logro
100%
Escritura de
numerales
Composición
Aditiva
Comprenden: Si escriben correctamente los numerales
Comprenden:
a. Componen correctamente numerales, en el rango:
b. Componen correctamente las unidades del sistema, sumando
numerales que exigen llevar, en el rango:
Composición
multiplicativa
Comprenden: Si resuelven correctamente problemas multiplicativos
gráficos, que exigen componer unidades en el período:
Descomposición
Multiplicativa
Comprenden:
a. Si resuelven correctamente problemas de descomposición de unidades
del sistema, en una unidad de orden inferior, en el rango de:
b. Si resuelven correctamente problemas de descomposición de unidades
en un período dado, en una unidad del mismo orden o de orden inferior,
en el rango de:
Secuencia de
unidades
Comprenden: Si son capaces de construir secuencias, en el rango de los
números entre 10 y 1.000, en los períodos de las decenas y las centenas
78
10 –100
Ítems 1 - 2
1 – 100
40+7
90+9
1 – 100
99+1
90+10
1 – 10
7×1
9×1
4×10
9×10
10 – 100
100/10
1 – 100
40/10
40/1
300/100
10 – 100
50%
100- 1.000
Ítems 3- 6
100 – 1.000
400+100
1 – 1.000
190+10
299+1
1 – 1.000
300/1
300/10
100 – 1.000
210 – 290
Cuadro 3. Criterios que permiten definir comprensión: Cuestionario 2
Componente
Criterio de logro
Escritura de
numerales
Composición
Aditiva
Comprenden: Si escriben
correctamente los numerales
Comprenden:
a. Componen correctamente
numerales, en el rango:
b. Componen correctamente las
unidades del sistema, sumando
numerales que exigen llevar, en el
rango:
Comprenden:
a. resuelven correctamente
problemas multiplicativos gráficos,
que exigen componer unidades en el
período:
b. resuelven correctamente
problemas multiplicativos verbales,
que exigen componer unidades en el
período:
Composición
multiplicativa
Descomposición
Multiplicativa
Éxito en función de grado
Rango y ejemplos para 3º
Rango y ejemplos para 4º
100%
50%
100%
50%
100 – 1.000
1.000 – 10.000 100 – 10.000
10.000 – 100.000
Ítems 1 – 4
Ítems 5- 8
Ítems 1 – 8
Ítems 8 – 12
1 – 10.000
>10.000
1 – 10.000
100 – 100.000
60+5+500+6.000 10.000+80+3
60+5+500+6.000
100.000+9.000+700
10.000+80+3
1 – 1.000
10 – 10.000
1 – 10.000
100 – 100.000
999+1
9.990+10
999+1
99.900+100
9.990+10
1 – 1.000
5×100
6×1.000
1 – 1.000
5×100
6×1.000
1-100
3×1
8×10
7×100
1 - 1.000
9×1.000
c. resuelven correctamente
problemas multiplicativos verbales
que exigen componer las unidades
del sistema
10 – 100
10×100
10 – 1.000
10×1.000
100×100
Comprenden:
a. Si resuelven correctamente
100 – 1.000
1.000/100
100 – 10.000
1 – 1.000
900/1
900/100
3.000/1.000
1 – 10.000
problemas de descomposición de
unidades del sistema, en una unidad
de orden inferior, en el rango de:
b. Si resuelven correctamente
problemas de descomposición de
unidades en un período dado, en
una unidad del mismo orden o de
orden inferior, en el rango de:
10.000/100
3.000/1
3.000/10
3.000/100
79
1 – 1.000
3×1
8×10
7×100
9×1.000
10 – 1.000
10×100
100×100
10×1.000
100 – 10.000
1.000/100
10.000/100
1 – 10.000
900/1
900/100
3.000/1
3.000/10
3.000/100
3.000/1.000
10 - 10.000
10×10.000
100 – 100.000
100.000/1.000
100.000/100
Componente
Descomposición
de numerales
Secuencia de
unidades
Criterio de logro
Éxito en función de grado
Rango y ejemplos para 3º
Rango y ejemplos para 4º
100%
50%
100%
50%
1.000 – 10.000 1.000 – 10.000
10.000 – 100.000
3.083
3.083
13.425
8.004
8.004
50.211
Comprenden: Si son capaces de
descomponer numerales en las
unidades que los forman o
componen, en el rango de:
Comprenden: Si son capaces de
1.000 – 10.000
construir secuencias, en el rango de 1.110 –1.190
los números entre 1.000 y 10.000, en 3.130 – 3.930
los períodos de las decenas y las
centenas
1.000 – 10.000
1.110 –1.190
3.130 – 3.930
80
Cuadro 4. Criterios que permiten definir comprensión: Cuestionario 3
Componente
Criterio de logro
Rango y ejemplos para 5º
100%
100 – 100.000
Ítems 1 – 12
1 – 100.000
Comprenden:
a. Componen correctamente numerales, en el rango:
60+5+500+6.000
10.000+80+3
100.000+9.000+700
b. Componen correctamente las unidades del sistema, sumando
100 – 100.000
numerales que exigen llevar, en el rango:
999+1
9.990+10
99.900+100
a. resuelven correctamente problemas multiplicativos verbales, que
1 – 10.000
Composición
exigen componer unidades en el período:
3×1
multiplicativa
8×10
7×100
9×1.000
10×10.000
c. resuelven correctamente problemas multiplicativos verbales que
10 – 10.000
exigen componer las unidades del sistema
10×100
100×100
Comprenden: Si resuelven correctamente problemas de descomposición 100 – 100.000
Descomposición
de unidades del sistema, en una unidad de orden inferior, en el rango de: 1.000/100
Multiplicativa
10.000/100
100.000/1.000
100.000/100
Comprenden: Si resuelven correctamente problemas de descomposición 100 – 10.000
de unidades en un período dado, en una unidad del mismo orden o de
900/1
orden inferior, en el rango de:
900/100
3.000/1
3.000/10
3.000/100
3.000/1.000
Descomposición de Comprenden: Si son capaces de descomponer numerales en las unidades 1.000 – 100.000
que los forman o componen, en el rango de:
3.083
numerales
8.004
13.425
50.211
Escritura de
numerales
Composición
Aditiva
10
Comprenden: Si escriben correctamente los numerales
Errores al escribir más del 50% de los ítems en el rango propio se considera dificultad moderada.
81
50%
100.000 – 1.000.000
Ítems 13 - 1610
Componente
Rango y ejemplos para 5º
Criterio de logro
100%
Secuencia de
unidades
Comprenden: Si son capaces de construir secuencias, en el rango de los
números entre 1.000 y 10.000, en los períodos de las decenas y las
centenas
82
1.000 – 10.000
1.110 –1.190
1.130 – 3.930
50%
Cuadro 5. Resumen de comprensión y dificultad
Componente:
Grado
Escritura de numerales
Comprenden
11
2º
59
Escriben correctamente numerales hasta 1.000
3º
31
Escriben correctamente numerales hasta 10.000
4º
5º
31
Escriben correctamente numerales hasta 100.000
24
Escriben correctamente numerales hasta 1.000.000
Componente:
Comprenden
2º
12
Componen correctamente unidades y numerales del
sistema hasta 1.000
Resuelven problemas aditivos del tipo: estado
transformación estado y composición de estados
Manejan el algoritmo de la suma en el rango definido
4º
5º
11
27
Escriben correctamente los numerales entre 10 y 100 y se
equivocan al escribir algunos numerales entre 100 y 1.000
45
Escriben correctamente los numerales entre 100 y 1.000 y se
equivocan al escribir algunos numerales entre 1.000 y 10.000
19
Escriben correctamente los numerales entre 1.000 y 10.000 y
se equivocan al escribir algunos numerales entre 10.000 y
100.000
21
Escriben correctamente los numerales entre 10.000 y 100.000
y se equivocan al escribir algunos numerales entre 100.000 y
1.000.000
14
Se equivocan al escribir numerales entre 10 y 100
Comprensión moderada
9
Componen correctamente unidades y numerales del sistema
hasta 100
Componen correctamente algunas unidades y numerales del
sistema entre 100 y 1.000
Resuelven problemas aditivos del tipo: estado transformación
estado y composición de estados
11
6
Componen correctamente unidades y numerales del sistema
Componen correctamente unidades del sistema y
hasta 1.000
numerales hasta 10.000
Componen correctamente algunas unidades y numerales del
Resuelven problemas aditivos del tipo: estado
sistema entre 1.000 y 10.000
transformación estado y composición de estados
Manejan el algoritmo de la suma en el rango definido Resuelven problemas aditivos del tipo: estado transformación
estado y composición de estados
5
13
Componen correctamente unidades y numerales del sistema
Componen correctamente unidades y numerales del
hasta 10.000
sistema hasta 100.000
Componen correctamente algunas unidades y numerales del
Resuelven problemas aditivos del tipo: estado
sistema entre 10.000 y 100.000
transformación estado y composición de estados
Manejan el algoritmo de la suma en el rango definido Resuelven problemas aditivos del tipo: estado transformación
estado y composición de estados
27
Componen correctamente unidades y numerales del
sistema hasta 1.000.000
Resuelven problemas aditivos del tipo: estado
transformación estado y composición de estados
Manejan el algoritmo de la suma en el rango definido
Componente:
Grado
Dificultad
24
Se equivocan al escribir los numerales entre 100 y
1.000
50
Se equivocan al escribir los numerales entre 1.000
y 10.000
54
Se equivocan al escribir los numerales entre
10.000 y 100.000
Composición aditiva
Grado
3º
Comprensión moderada
Dificultad
79
No componen correctamente algunas unidades y
numerales del sistema hasta 100
83
No componen correctamente algunas unidades y
numerales del sistema hasta 1.000
82
No componen correctamente algunas unidades y
numerales del sistema hasta 10.000
73
No componen correctamente unidades y
numerales del sistema hasta 100.000
Composición multiplicativa
Comprenden
Comprensión moderada
Para fines de presentación los porcentajes de aciertos se aproximan.
83
Dificultad
Grado
2º
3º
4º
5º
Comprenden
Comprensión moderada
Dificultad
43
Resuelven correctamente problemas de
composición multiplicativa de unidades en
el período de las decenas
Resuelve correctamente problemas
multiplicativos del tipo proporción simple
13
Resuelven correctamente problemas de
composición multiplicativa de unidades en
los períodos comprendidos entre 1 y 1.000,
presentados en formato gráfico
Resuelven correctamente problemas de
composición multiplicativa de unidades del
sistema hasta 1.000 y de unidades en los
periodos de las centenas y las unidades de
mil, presentados en formato verbal
Resuelven correctamente problemas
multiplicativos del tipo proporción simple
26
Resuelven correctamente problemas de
composición multiplicativa de unidades en
los períodos comprendidos entre 1 y 1.000,
presentados en formato gráfico
Resuelven correctamente problemas de
composición multiplicativa de unidades en
los períodos comprendidos entre 1 y 1.000,
presentados en formato verbal
Resuelven correctamente problemas de
composición multiplicativa de unidades del
sistema, hasta 10.000, presentados en
formato verbal
Resuelven correctamente problemas
multiplicativos del tipo proporción simple
50
Resuelven correctamente problemas de
composición multiplicativa de unidades en
los períodos comprendidos entre 1 y
10.000, presentados en formato verbal
Resuelven correctamente problemas de
composición multiplicativa de unidades del
sistema, hasta 10.000, presentados en
formato verbal
Resuelven correctamente problemas
multiplicativos del tipo proporción simple
-
57
No resuelven correctamente algún problema
de composición multiplicativa de unidades
en el período de las decenas
10
Resuelven correctamente problemas de composición
multiplicativa de unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato gráfico
Resuelven correctamente problemas de composición
multiplicativa de unidades del sistema hasta 100 y de
unidades en los periodos de las centenas, presentados en
formato verbal
Resuelven correctamente algunos problemas multiplicativos
verbales del tipo proporción simple hasta 1.000
Resuelven correctamente problemas multiplicativos del tipo
proporción simple
2
Resuelven correctamente problemas de composición
multiplicativa de unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato gráfico
Resuelven correctamente problemas de composición
multiplicativa de unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato verbal
Resuelven correctamente problemas de composición
multiplicativa de unidades del sistema hasta 1.000,
presentados en formato verbal
Resuelven correctamente algunos problemas de
composición multiplicativa de unidades del sistema hasta
10.000, presentados en formato verbal
Resuelven correctamente problemas multiplicativos del tipo
proporción simple
-
77
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato
gráfico
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades del sistema hasta 100 y de
unidades en el periodo de las centenas,
presentados en formato verbal
Componente:
Grado
72
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato
gráfico
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades en los períodos comprendidos
entre 1 y 1.000, presentados en formato
verbal
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades del sistema hasta 1.000,
presentados en formato verbal
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades en los períodos comprendidos
entre 1 y 10.000, presentados en formato
verbal
No resuelven correctamente algunos
problemas de composición multiplicativa de
unidades del sistema, hasta 10.000,
presentados en formato verbal
Descomposición multiplicativa
Comprenden
Comprensión moderada
84
Dificultad
Grado
2º
3º
4º
5º
Comprenden
4
Resuelven correctamente problemas de descomposición de la
centena en unidades de orden inferior
Resuelven correctamente problemas de descomposición de
unidades en el período de las decenas en la unidad del mismo
orden y de orden inferior
Resuelven correctamente problemas de descomposición de
unidades en los período de las centenas en unidades del mismo
orden
Resuelven correctamente algunos problemas de descomposición
de unidades en el período de las centenas en unidades de orden
inferior
Resuelven correctamente problemas de división
17
Resuelven correctamente problemas de descomposición de la
unidad de mil en centenas
Resuelven correctamente problemas de descomposición de
unidades en el período de las centenas en la unidad del mismo
orden y unidades de orden inferior
Resuelven correctamente problemas de descomposición de
unidades en el período de las unidades de mil en unidades del
mismo orden
Resuelven correctamente algunos problemas de descomposición
de la decena de mil en centenas
Resuelven correctamente algunos problemas de descomposición
de unidades en el período de las unidades de mil en unidades de
orden inferior
Resuelven correctamente problemas de división
6
8
Resuelven correctamente problemas de Resuelven correctamente problemas de descomposición de
descomposición de unidades, decenas y unidades y decenas de mil en unidades de mil y centenas
centenas de mil en unidades de mil y
Resuelven correctamente problemas de descomposición de
centenas
unidades en el período de las centenas y las unidades de mil en
Resuelven correctamente problemas de unidades del mismo orden y de orden inferior
descomposición de unidades en el
Resuelven correctamente algunos de los problemas de
período de las centenas y las unidades
descomposición de centenas de mil en unidades de mil y
de mil en unidades del mismo orden y
centenas
de orden inferior
Resuelven correctamente problemas de división
Resuelven correctamente problemas de
división
16
Resuelven correctamente problemas de
descomposición de unidades, decenas y
centenas de mil en unidades de mil y
centenas
Resuelven correctamente problemas de
descomposición de unidades en el
período de las centenas y en el de las
unidades de mil en unidades del mismo
orden y de orden inferior
Resuelven correctamente problemas de
división
Componente:
Grado
Comprensión moderada
2
Resuelven correctamente problemas de
descomposición de la centena en
unidades de orden inferior
Resuelven correctamente problemas de
descomposición de unidades en los
período de las decenas y centenas en
unidades del mismo orden y de orden
inferior
Resuelven correctamente problemas de
división
Dificultad
94
No resuelven correctamente problemas de
descomposición de unidades en el período
de las decenas en la unidad del mismo
orden y de orden inferior
83
No resuelven correctamente algunos
problemas de descomposición de la
unidad de mil en centenas
No resuelven correctamente algunos
problemas de descomposición de unidades
en el período de las centenas en la unidad
del mismo orden y unidades de orden
inferior
No resuelven correctamente algunos
problemas de descomposición de unidades
en el período de las unidades de mil en
unidades del mismo orden
86
No resuelven correctamente algunos
problemas de descomposición de unidades
y decenas de mil en unidades de mil y
centenas
No resuelven correctamente algunos
problemas de descomposición de unidades
en el período de las centenas y las
unidades de mil en unidades del mismo
orden y de orden inferior
84
No resuelven correctamente algunos
problemas de descomposición de
unidades, decenas y centenas de mil en
unidades de mil y centenas
No resuelven correctamente algunos
problemas de descomposición de unidades
en el período de las centenas y en el de las
unidades de mil en unidades del mismo
orden y de orden inferior
Descomposición de numerales
Comprenden
Comprensión moderada
85
Dificultad
Grado
3º
4º
5º
Comprenden
14
Descomponen correctamente numerales
en el rango de 1.000 a 10.000
12
Descomponen correctamente numerales
en el rango de 1.000 a 100.000
12
Descomponen correctamente numerales
en el rango de 1.000 a 100.000
Componente:
Grado
2º
3º
4º
5º
Comprensión moderada
86
Descomponen correctamente algunos numerales en el rango de
1.000 a 10.000
85
Descomponen correctamente numerales en el rango de 1.000 a
10.000 y algunos en el rango de 10.000 a 100.000
Dificultad
3
Se equivocan al descomponer algunos
numerales en el rango de 1.000 a 10.000
34
Se equivocan al descomponer algunos
numerales en el rango de 1.000 a 100.000
Secuencia de unidades
Comprenden
77
Son capaces de construir secuencias en
el rango de las decenas
Son capaces de construir secuencias en
el rango de los números entre 100 y
1.000 en el período de las decenas
40
Son capaces de construir secuencias en
el rango de los números entre 1.000 y
10.000 en los períodos de las decenas y
las centenas
56
Son capaces de construir secuencias en
el rango de los números entre 1.000 y
10.000 en los períodos de las decenas y
las centenas
70
Son capaces de construir secuencias en
el rango de los números entre 1.000 y
10.000 en los períodos de las decenas y
las centenas
Comprensión moderada
Dificultad
15
Son capaces de construir secuencias en el rango de las decenas
Son capaces de construir algunas secuencias en el rango de los
números entre 100 y 1.000 en el período de las decenas
8
Se equivocan al construir secuencias en el
rango de las decenas
60
Son capaces de construir algunas secuencias en el rango de los
números entre 1.000 y 10.000 en los períodos de las decenas y
las centenas
-
-
-
86
44
Se equivocan al construir algunas
secuencias en el rango de los números
entre 1.000 y 10.000 en los períodos de las
decenas y las centenas
30
Se equivocan al construir algunas
secuencias en el rango de los números
entre 1.000 y 10.000 en los períodos de las
decenas y las centenas
Tabla 3. Niveles de dificultad por componente, según grado
Grado
Composición
aditiva
%
Escritura
%
Comp.12
Cm13 Dif14
Composición
Multiplicativa
%
Comp
Cm
Dif
Comp Cm Dif
-
56,6
Descomposición
multiplicativa
%
Descomposición
numerales
%
Secuencia de
unidades
%
Comp
Cm
Dif
Comp
Cm
Dif
Comp
Cm
Dif
2,1
3,7
94,2
-
-
-
77,2
15,1
7,7
17,1 82,9
13,9
86,1
40,4
59,6
-
2°
59,0
26,8
14,2
12,4
8,6
79,0
43,4
3°
30,8
45,2
24,0
5,7
11,5
82,9
12,5
10,4 77,1
4°
30,9
19,0
50,1
12,8
5,5
81,7
26,3
2,3
71,4
6,5
7,8
85,7
12,6
84,7
2,7
55,6
-
44,4
5°
24,5
21,3
54,2
27,1
-
72,9
49,9
-
50,1
16,0
-
84,0
11,2
-
88,8
70,6
-
29,4
Comprende
Comprensión moderada
14
Dificultad
12
13
87
-
Aciertos de 2º al contestar el cuestionario 1
Gráfico 2: Acierto en la secuencia de unidades
Grafico 1: Acierto al escribir numerales con y sin
cero
1
1
0,9
0,9
0,8
0,8
0,7
0,7
0,6
0,6
0,5
0,5
0,4
0,4
0,3
0,3
0,2
0,2
0,1
0,1
0
0
89
325
987
Sin cero
1.452 8.967
90
201
908
3.004 9.070
Decenas + 10
Con cero
Centenas + 100
Secuen unid
88
Centenas + 10
Gráfico 3: Aciertos en la composición aditiva y composición y descomposición multiplicativa
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
99+1
90+10
Comp adit unid
40+7
90+9
199+1
299+1
Comp adit num
400+100
9x10
10x4
7x1
Comp mult num gráfico
89
9x1
100/10
Des mult
unid sist
40/10
40/1
300/100
300/10
Descom mult unid período
300/1
Aciertos de 3º 4º y 5º al contestar el cuestionario 2 y 3
Gráfico 5: Acierto en descomposición de numerales y
secuencia de unidades
Gráfico 4: Aciertos al escribir numerales con y sin
cero
1
1
0,9
0,9
0,8
0,8
0,7
0,7
0,6
0,6
0,5
0,5
0,4
0,4
0,3
0,3
0,2
0,2
0,1
0,1
0
Sin cero
8.004
800.009
104.002
85.007
20.103
9.070
3.004
908
201
987.658
543.152
97.586
34.243
8.967
1.452
987
325
0
4o
13.425
50.211
Descom numeral
Con cero
3o
3.083
5o
3o
90
Secuencia Secuencia
Numérica Numerica
Decena
Centenas
Secuen unid
4o
5o
Gráfico 6: Acierto en la composición aditiva y composición y descomposición multiplicativa
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
Comp adit unid Comp adit num
Comp
Comp
mult unid mult num
gráfico
Comp mult num verbal
3o
23
4o
5o
Descom mult unid
sist
3.000/1
3.000/10
3.000/100
3.000/1,000
900/100
900/1
100.000/100
100.000/1.000
10.000/100
1.000/100
10x10.000
9x1.000
7x100
10x1.000
8x10
3x1
6x1.000
5x100
100x100
10x100
100.000+9.000+700
10.000+80+3
6.000+500+60+5
99.900+100
9.990+10
999+1
0
Descom mult unid período
Gráfico 7: Distribución de alumnos de 2o según
intervalos de acierto
Gráfico 8: Distribución de alumnos de 3o según
intervalos de acierto
40%
40%
35%
35%
30%
30%
25%
25%
20%
20%
15%
15%
10%
10%
5%
5%
0%
1-5
6-9
10-13
14-17
18-21
22-25
26-30
0%
Gráfico 9: Distribución de alumnos de 4o según
intervalos de acierto
40%
1-6
7-13
14-20
21-27
28-34
35-41
42-48
Gráfico 10: Distribución de alumnos de 5o. según
intervalos de acierto
40%
35%
35%
30%
30%
25%
25%
20%
20%
15%
15%
10%
10%
5%
5%
0%
1-6
7-13
14-20
21-27
28-34
35-41
0%
42-48
24
6-12
13-18
19-25
26-32
33-39
40-46
Gráfico 11 : Comprensión versus dificultad grado 2o
Comprende
39%
Dificultad
50%
comprensión
moderada
11%
Gráfico 12: Comprensión versus dificultad grado
3o
Comprende
17%
Dificultad
45%
Comprensión
moderada
38%
25
Gráfico 13: Comprensión versus dificultad grado
4o
Comprende
24%
Dificultad
56%
comprensión
moderada
20%
Gráfico 14: Comprensión y difcultades grado 5o
Comprende
33%
Dificultad
63%
Comprensión
moderada
4%
26
Comprende
Escritura
Composición
aditiva
Composición
multiplicativa
27
Descomp multi
Descomp
numérica
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Gráfico 15: Comprensión de 2o según componentes
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Secuencia
numerica
Comprende
Escritura
Composición
aditiva
Composición
multiplicativa
28
Descomp multi
Descomp
numérica
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Gráfica 16: Comprensión de 3o según componentes
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Secuencia
numerica
Comprende
Escritura
Composición
aditiva
Composición
multiplicativa
29
Descomp multi
Descomp
numérica
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Comprende
Dificultad
Comprensión moderada
Gráfica 17: Comprensión de 4o según componentes
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Secuencia
numerica
Gráfica 18: Comprensión de 5o según componentes
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Esc ritura
Composición
aditiva
Composic ión
multiplic ativa
30
Descomp multi
Desc omp
numérica
Sec uencia
numeric a


