Códigos convolucionales - Luca Martino Home Page
Anuncio

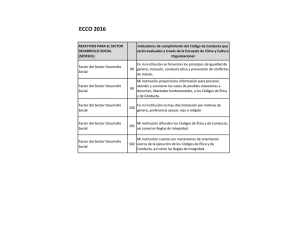
Códigos convolucionales – Prac3ca 3 Luca Mar3no Apuntes-­‐Laboratorio no revisados (cuidado!!!) Repaso 1-­‐ obje3vos de la transmisión digital de la información • Transmisión fiable control de errores codificación de canal. • Transmisión rápida (“ligera”) compresión codificación de fuente. • Transmisión segura auten3cidad, privacidad criptograKa. Códigos Convolucionales • Se trata de codificación de canal: añadir redundancia para lograr una trasmisión fiable de la información. • Los códigos convolucionales son códigos lineales, donde la suma de dos palabras de código cualesquiera también es una palabra de código. • Se diferencian de los códigos bloque en su forma estructural y las propiedades para corregir errores. • Tienen memoria: la codificación actual depende de los datos que se envían ahora y que se enviaron en el pasado. Códigos Convolucionales • Un código convolucional queda especificado por tres parámetros: Bits de información • Números de entradas k • Números de salidas n Secuencia codificada de información, bits de información + bit de redundancia. • Memoria de código m k R= n € Tasa del código Códigos Convolucionales -­‐ filtro FIR • Un código convolucional es un filtro FIR binario (es una convolución…). • La salida se ob3ene filtrando la secuencia de entrada con un filtro FIR binario. Representación • Pueden representarse de diferentes formas: • Registros de desplazamiento. • Sistema de n ecuaciones (binarias) con m incógnitas (filtro FIR). • Tabla de relación entrada/salida (filtro FIR). • Polinomios (parecido a la trasformada Zeta…). • Diagrama de árbol. • Diagrama de estados (maquinas de estados finitos). • Diagrama Trellis. Ejemplo con registros de desplazamiento • Se cosidere un código convolucional m=3 n =2 k =1 registros salidas entradas k 1 R= = n 2 Salida 1-­‐ O1 (output 1) € Secuencia € en entrada Desde el bit más an3guo… € S1 S2 S3 € Salida 2-­‐ O2 (output 2) € € € € se considera que • Al principio S1 = 0 S2 = 0 S3 = 0 tasa O1O 2 Ejemplo con registros de desplazamiento • Los bits ingresan por la izquierda y salen por la derecha, pero los bits de una palabra se leen de izquierda a derecha. • Observación importante: si queremos codificar 1010 tenemos que dar la vuelta a la secuncia para empezar desde el más an3guo: 0101 (4 bits en entrada) € € Ejemplo con registros de desplazamiento • Supongamos que queremos enviar y codificar la secuencia 0101 O1 0101 0 0 0 O2 € € € O1O€2 € € € • Recordamos que al principio los registros son nulos € S1 = 0 S2 = 0 S3 = 0 Ejemplo con registros de desplazamiento • Entra el primer bit – 1 O1 = 1+ 0 = 1 010 1 0 0 € € € € ....11 • p€roducimos € € O 2 = 1+ 0 = 1 € O1O 2 = 11 Ejemplo con registros de desplazamiento • Desplazamos el primer bit – 1 y entra el segundo -­‐ 0 O1 = 0 + 0 = 0 01 0 1 0 O 2 = 0 +1 = 1 € € € toda € la salida hasta ahora es • e€s decir € ....01 −11€ € O1O 2 = 01 Ejemplo con registros de desplazamiento • Desplazamos todo y entra el bit -­‐ 1 O1 = 1+1 = 0 0 1 0 1 O 2 = 1+ 0 = 1 € € € toda € la salida hasta ahora es • e€s decir € ....01 − 01 −11 € € O1O 2 = 01 Ejemplo con registros de desplazamiento • Finalmente O1 = 0 + 0 = 0 0 1 O1O 2 = 01 0 O 2 = 0 +1 = 1 € € € es codificada como (esta es la salida final de 8 bits) • L€a secuencia € 01 − 01 − 01€ −11 € Sistema de ecuaciones (en binario) • Claramente lo que hemos hecho hasta ahora se puede expresar como O1 ⎧ O1 = S1 + S3 ⎨ ⎩O 2 = S1 + S2 S1 S2 S3 € € € € € € O2 € Tabla entradas/salidas • Claramente lo que hemos hecho hasta ahora se puede expresar como Respuesta impulsiva € S1S2 S3 O1O 2 000 100 00 € m 3 2 = 2 =€8 € € € € € € S1 S2 11 010 €001 € 110 € 011 € 101 € 111 € € € € O1 01 10 10 11 01 00 S3 € € € € € O2 Polinomios • Como una trasformada Zeta pero con potencias posi3vas O1(x) S1 →1 S2 → x g1(x) = 1+ x 2 g2 (x) = 1+ x S3 → x 2 € € m(x) S1 S2 S3 € O 2 (x) • Si por ejemplo queremos € enviar 0101 →m(x) = 0⋅ 1+ € x + 0⋅€ x 2 € + x3 = x + x3 € € 3 2 3 3 O1(x) = m(x)g1 (x) = x + x 1+ x = x + x + x + x 5 = x + x 5 ( )( ) O (x) = m(x)g (x) = ( x + x )(1+ x ) = x + x € 3 2 1 3 + x2 + x4 = x + x2 + x3 + x4 Árbol Salidas O1 y O2 CUIDADO!!! El orden está inver3do !!! Aquí es S3,S2,S1 Salidas O1 y O2 Estados del Trellis o de la maquina de estados finitos.