Tema 3. Circuitos Resistivos
Anuncio

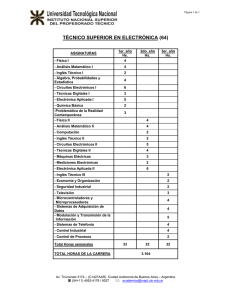
Tema 3. Circuitos Resistivos 1 Sistemas y Circuitos © Francisco J. González, UC3M 2009 3.1 Elementos en Circuitos i (t ) Elementos de circuitos + • Dos terminales v(t ) Tanto la tensión como la corriente son variables que tienen signo. z Dispositivo (R, L,C) (Generador) − • Potencia (instantánea) i (t ) + p(t ) = v(t )i (t ) 3A Si p(t)<0, el dispositivo genera − 5V p (t ) = −15 W © Francisco J. González, UC3M 2009 -5 V p (t ) = −15 W + − Consume − Dispositivo (R, L,C) (Generador) − + p (t ) = 15 W v (t ) −3 A 3A + 5V Si p(t)>0, el dispositivo consume Genera Sistemas y Circuitos Genera 2 3.1 Elementos en Circuitos Activos • Generadores ideales: mantienen su valor nominal independientemente de lo que haya conectado a sus terminales − Tensión v(t ) + VS − constante + − − Corriente i (t ) 5V 5A + − Tanto la tensión como la corriente son variables que tienen signo. 2A z 2A Permitido © Francisco J. González, UC3M 2009 No Permitido 3 Sistemas y Circuitos 3.1 Elementos en Circuitos Activos • Generadores dependientes: − su valor nominal depende de otra magnitud en el circuito • Generadores de tensión dependientes de Tensión α vx (t ) + Corriente − ρ iy (t ) + − • Generadores de corriente dependientes de Corriente β is (t ) © Francisco J. González, UC3M 2009 Tensión μ vr (t ) Sistemas y Circuitos 4 3.1 Elementos en Circuitos Pasivos • Relaciones tensión-corriente en Tanto la tensión como la corriente son variables que tienen signo. − Resistencias (ley de Ohm) + v(t ) + + i (t ) 0.5 A R 10RΩ 5V −0.5 A − − 10RΩ 5V − v(t ) = Ri (t ) + − 0.5 A −5 V 10RΩ 10 RΩ 5V + − © Francisco J. González, UC3M 2009 0.5 A 5 Sistemas y Circuitos 3.1 Elementos en Circuitos Pasivos • Relaciones tensión-corriente en − Resistencias (ley de Ohm) + i (t ) v(t ) = Ri (t ) v(t ) R 400 − v(t ) = 220 2 sin(2π 50t ) V 300 200 100 R = 10Ω i (t ) = 22 2 sin(2π 50t ) A 0 -100 -200 -300 -400 © Francisco J. González, UC3M 2009 0 0.01 0.02 0.03 Sistemas y Circuitos 0.04 0.05 0.06 0.07 0.08 0.09 0.1 6 3.1 Elementos en Circuitos Pasivos 400 200 − Resistencias (ley de Ohm) 100 i (t ) + 0 i (t ) v(t ) = Ri (t ) v(t ) 300 • Relaciones tensión-corriente en v(t ) -100 R -200 -300 − -400 v(t ) = 220 2 sin(2π 50t ) V 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 10000 p (t ) R = 10Ω 8000 i (t ) = 22 2 sin(2π 50t ) A 6000 v 2 (t ) 2 p (t ) = v(t )i (t ) = = i (t ) R [W] R Consume 4000 p(t)>0, 2000 » resistencias siempre consumen 0 -2000 © Francisco J. González, UC3M 2009 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 7 Sistemas y Circuitos 3.1 Elementos en Circuitos Circuitos • Nodos (nudos), ramas, lazos y mallas Rama esencial: Rama une dos nodos esenciales Malla L1 L2 R2 v(t ) + C2 C3 R1 − Lazo L3 C4 C1 Nodo Nodo esencial: punto donde se conectan tres o más elementos © Francisco J. González, UC3M 2009 Sistemas y Circuitos 8 3.2 Resolución mediante Lemas Kirchhoff Resolución de circuitos • Obtener los valores de la corriente en cada rama y/o del voltaje en cada nodo Ley de Corrientes de Kirchhoff (LCK) • “La suma algebraica de todas las corrientes en un nodo es 0 A” ia ia − ib − ic − id = 0 ib id ic −ia + ib + ic + id = 0 Corrientes entrantes (+) Corrientes de salida (-) Corrientes entrantes (-) Corrientes de salida (+) ia = ib + ic + id Suma Corrientes entrantes = Suma Corrientes de salida © Francisco J. González, UC3M 2009 9 Sistemas y Circuitos 3.2 Resolución mediante Lemas Kirchhoff Resolución de circuitos • Obtener los valores de la corriente en cada rama y/o del voltaje en cada nodo Ley de Corrientes de Kirchhoff (LCK) • “La suma algebraica de todas las corrientes en un nodo es 0 A” −3A 12A 1A Corrientes entrantes (+) Corrientes de salida (-) −3 − 12 + 16 − 1 = 0 −16A 3 + 12 − 16 + 1 = 0 Corrientes entrantes (-) Corrientes de salida (+) −3 = 1 + 12 − 16 Suma Corrientes entrantes = Suma Corrientes de salida © Francisco J. González, UC3M 2009 Sistemas y Circuitos 10 3.2 Resolución mediante Lemas Kirchhoff Resolución de circuitos • Obtener los valores de la corriente en cada rama y/o del voltaje en cada nodo Ley de Voltajes (Tensiones) de Kirchhoff (LVK) • “La suma algebraica de todas las tensiones en un lazo es 0 V” − El sentido en el que se recorre el lazo es arbitrario. vL 3 (t ) + vC 2 (t ) + vL 2 (t ) − vC1 (t ) = 0 Subidas tensión (+) L1 R2 vC 2 (t ) C2 −vL 3 (t ) − vC 2 (t ) − vL 2 (t ) + vC1 (t ) = 0 + + vL 3 (t ) L2 vL 2 (t ) − C4 Bajadas tensión (-) − + + L3 vC1 (t ) − − Subidas tensión (+) Bajadas tensión (-) vC1 (t ) = vL 3 (t ) + vC 2 (t ) + vL 2 (t ) C1 Suma caídas tensión = Suma subidas de tensión © Francisco J. González, UC3M 2009 11 Sistemas y Circuitos 3.3 Circuitos resistivos Resistencia equivalente • Serie: R1 I R2 R3 + V1 = IR1 − +V2 = IR2 − + RN + VN − V3 − − Ley de Tensiones de Kirchhoff I Req + N ∑ k =1 − Vk = I ( R1 + R2 + Req = R1 + R2 + © Francisco J. González, UC3M 2009 + RN ) = IReq N + RN = ∑ Rk Sistemas y Circuitos k =1 12 3.3 Circuitos resistivos Resistencia equivalente • Paralelo: Ley de Corrientes de Kirchhoff + V − I R1 R2 R3 + V − RN Req = 1 1 1 + + R1 R2 I ⎛1 1 V⎜ + + ⎝ R1 R2 Req 1 + RN = + 1 ⎞ V ⎟= RN ⎠ Req 1 N ∑ k =1 1 Rk − Paralelo de dos resistencias R1 Req R2 © Francisco J. González, UC3M 2009 Req = 1 RR = 1 2 1 1 R 1 + R2 + R1 R2 Sistemas y Circuitos 13 3.3 Circuitos resistivos Circuito divisor de tensión R1 + + R2 V V2 − − V2 = ⎛ R2 ⎞ V R2 = ⎜ ⎟V R1 + R2 ⎝ R1 + R2 ⎠ ⎛ R2 ⎞ ⎜ ⎟ ≤1 ⎝ R1 + R2 ⎠ © Francisco J. González, UC3M 2009 Sistemas y Circuitos 14 3.3 Circuitos resistivos Circuito divisor de corriente I I1 I1 + I 2 = I R1 I2 R2 I1 R1 = I 2 R2 R I1 + I1 1 = I R2 ⎛ R2 ⎞ I1 = ⎜ ⎟I ⎝ R1 + R2 ⎠ ⎛ R1 ⎞ I2 = ⎜ ⎟I R + R 2 ⎠ ⎝ 1 ⎛ R2 ⎞ ⎜ ⎟ ≤1 ⎝ R1 + R2 ⎠ © Francisco J. González, UC3M 2009 ⎛ R1 ⎞ ⎜ ⎟ ≤1 ⎝ R1 + R2 ⎠ Sistemas y Circuitos 15 Signo en voltajes ¿Por qué un voltaje puede ser negativo? © Francisco J. González, UC3M 2009 Sistemas y Circuitos 16 Elementos en circuitos Resistores + i (t ) v(t ) = Ri (t ) v(t ) R − © Francisco J. González, UC3M 2009 Sistemas y Circuitos 17 Elementos en circuitos Bobinas… + v(t ) i(t ) L − v(t ) = L di(t ) dt © Francisco J. González, UC3M 2009 Sistemas y Circuitos 18 Elementos en circuitos Condensadores v(t ) + − i(t ) = C i(t ) C dv(t ) dt © Francisco J. González, UC3M 2009 19 Sistemas y Circuitos 3.4 Resolución de circuitos Método de las tensiones en nodos 1. Marcar y etiquetar los nodos esenciales a R1 v(t ) + + − Datos: v(t ), i (t ), R1, R 2, R3, R 4 + R2 va − b R3 c vb R4 i (t ) − 2. Elegir nodo de referencia (su voltaje relativo es 0 V) Generalmente, se elige aquel al que se conectan más ramas 3. Definir voltajes en nodos respecto al nodo de referencia 4. Aplicar Ley de corrientes de Kirchhoff en cada nodo © Francisco J. González, UC3M 2009 Sistemas y Circuitos 20 3.4 Resolución de circuitos Método de las tensiones en nodos 4. Aplicar Ley de corrientes de Kirchhoff en cada nodo a R1 + V + + R2 va − − R1 + + i1 V − a R4 vb I − c R3 + i R2 3 va b R3 Nodo a: vb i2 − − i1 − i2 + i3 = 0 V − va v i1 = i2 = a R1 R2 i3 = ⎛ 1 ⎛ 1 ⎞ V 1 1 ⎞ + ⎟ − vb ⎜ ⎟ = va ⎜ + R R R 2 3 ⎠ ⎝ 1 ⎝ R3 ⎠ R1 1 ecuación, 2 incógnitas © Francisco J. González, UC3M 2009 vb − va R3 21 Sistemas y Circuitos 3.4 Resolución de circuitos Método de las tensiones en nodos 4. Aplicar Ley de corrientes de Kirchhoff en cada nodo a R1 + V + + R2 va − − R3 + + i3 va − Nodo b: R4 i4 − © Francisco J. González, UC3M 2009 c vb R4 I − I b vb b R3 I − i3 − i4 = 0 v −v v i3 = b a i4 = b R3 R4 ⎛ 1 ⎞ ⎛ 1 1 ⎞ −va ⎜ ⎟ + vb ⎜ + ⎟ = I ⎝ R3 ⎠ ⎝ R3 R4 ⎠ 1 ecuación, 2 incógnitas Sistemas y Circuitos 22 3.4 Resolución de circuitos Método de las tensiones en nodos 5. Resolver ecuaciones Nº Ecuaciones = Nº nodos esenciales -1 R1 R3 a b + V + + R2 va − − I − c ⎛ 1 ⎛ 1 ⎞ V 1 1 ⎞ va ⎜ + + ⎟ − vb ⎜ ⎟ = ⎝ R1 R2 R3 ⎠ ⎝ R3 ⎠ R1 Si conocemos va y vb conoceremos todas las tensiones y corrientes en el circuito ⎛ 1 ⎞ ⎛ 1 1 ⎞ −va ⎜ ⎟ + vb ⎜ + ⎟ = I ⎝ R3 ⎠ ⎝ R3 R4 ⎠ © Francisco J. González, UC3M 2009 R4 vb 23 Sistemas y Circuitos 3.4 Resolución de circuitos Método de las corrientes en mallas 1. Marcar y etiquetar las mallas R1 v(t ) + − Datos: v(t ), i (t ), R1, R 2, R3, R 4 R3 Ia Malla a R2 R4 Ib Ic Malla b i (t ) Malla c 2. Definir corrientes de malla Se elige arbitrariamente el sentido en el que circulan 3. Aplicar Ley de tensiones de Kirchhoff en cada malla 4. Resolver ecuaciones © Francisco J. González, UC3M 2009 Nº Ecuaciones = Nº Mallas Sistemas y Circuitos 24 3.4 Resolución de circuitos Método de las corrientes en mallas 3. Aplicar Ley de tensiones de Kirchhoff en cada malla R1 V R3 + − Ia Datos: v(t ), i (t ), R1, R 2, R3, R 4 Malla a Malla a: Malla b: Malla c: R2 R4 Ib Ic Malla b Malla c 4. −V + I a R1 + ( I a − I b ) R2 = 0 ( I b − I a ) R2 + Ib R3 + ( Ib − I c ) R4 = 0 Ic = −I I Resolver ecuaciones I a ( R1 + R2 ) − I b R2 = V − I a R2 + I b ( R2 + R3 + R4 ) = − IR4 2 ecuaciones, 2 incógnitas 3 ecuaciones, 3 incógnitas © Francisco J. González, UC3M 2009 25 Sistemas y Circuitos 3.5 Transformación de generadores Transformación de generadores : • Procedimiento por el cual una fuente de tensión en serie con una resistencia se transforma en un generador de corriente en paralelo con un resistencia. • El comportamiento de ambos circuitos respecto de los terminales a y b es idéntico. i RS i a a VS + VS = I S RP vab IS RP RS = RP vab b b Pendiente -RS vab Cortocircuito (vab=0) Circuito abierto (i=0) VS RS © Francisco J. González, UC3M 2009 vab VS Característica v-i i Pendiente -RP Característica v-i I S RP Cortocircuito (vab=0) i IS Sistemas y Circuitos 26 3.6 Superposición Linealidad en circuitos resisitivos Anulamos el generador de corriente→ 0 A.⇔ circuito abierto Anulamos el generador de tensión→ 0 V ⇔ cortocircuito i1 = i1′ + i1′′ © Francisco J. González, UC3M 2009 27 Sistemas y Circuitos 3.7 Equivalente de Thèvenin Un circuito lineal conteniendo resistencias y generadores dependientes y/o independientes puede reemplazarse por un generador independiente de tensión en serie con una resistencia • Tensión y resistencia de Thèvenin Circuito A a RTH VTH RL + − b © Francisco J. González, UC3M 2009 ia RL b Sistemas y Circuitos 28 3.7 Equivalente de Thèvenin Un circuito conteniendo resistencias y generadores independientes y/o dependientes puede reemplazarse por un generador independiente de tensión en serie con una resistencia. Circuito A a ia RTH VTH RL + − I SC RL b b Procedimiento 1. Calcular la tensión en circuito abierto: Vab = VTH 2. Calcular la corriente en cortocircuito: Iab = ISC V 3. La resistencia deThèvenin es RTH = IOC SC © Francisco J. González, UC3M 2009 29 Sistemas y Circuitos 3.7 Equivalente de Norton Un circuito lineal conteniendo resistencias y generadores dependientes y/o independientes puede reemplazarse por un generador independiente de corriente en paralelo con una resistencia • Corriente y resistencia de Norton Circuito A a i a RL RN RL b b © Francisco J. González, UC3M 2009 IN Sistemas y Circuitos 30 3.7 Equivalente de Norton Un circuito conteniendo resistencias y generadores independientes y/o dependientes puede reemplazarse por un generador independiente de corriente en paralelo con una resistencia. Circuito A a i a IN RL RN RL b b Procedimiento 1. Calcular la corriente en cortocircuito: ISC = IN 2. Calcular la tensión en circuito abierto: VAB = IN RN V 3. La resistencia de Norton es RN = OC IN © Francisco J. González, UC3M 2009 31 Sistemas y Circuitos 3.7 Equivalente Thèvenin Máxima transferencia de potencia: • ¿Cuánto ha de valer RL para que la potencia que disipe sea máxima? RTH VTH ia + − RL b PRL 2 ⎛ VTH ⎞ PRL = ⎜ ⎟ RL ⎝ RTH + RL ⎠ PRL MAX 0 © Francisco J. González, UC3M 2009 RL , MAX RL Sistemas y Circuitos 32 3.7 Equivalente Thèvenin Máxima transferencia de potencia: • ¿Cuánto ha de valer RL para que la potencia que disipe sea máxima? RTH VTH ia 2 + − RL ⎛ VTH ⎞ PRL = ⎜ ⎟ RL ⎝ RTH + RL ⎠ b PRL ⎛ ( R + RL )2 − RL i2 ( RTH + RL ) ⎞ = VTH2 ⎜ TH ⎟ 4 ⎜ ⎟ dRL ( RTH + RL ) ⎝ ⎠ dPRL 2 = 0 → ( RTH + RL ) − RL i2 ( RTH + RL ) = 0 dRL dPRL dPRL dRL =0 dPRL 0 © Francisco J. González, UC3M 2009 RTH RL dRL = 0 → RTH = RL Sistemas y Circuitos 33 3.7 Equivalente Thèvenin © Francisco J. González, UC3M 2009 Sistemas y Circuitos 34 Ejercicios de Repaso © Francisco J. González, UC3M 2009 Sistemas y Circuitos 35 Ejercicios de Repaso © Francisco J. González, UC3M 2009 Sistemas y Circuitos 36 Ejercicios de Repaso © Francisco J. González, UC3M 2009 Sistemas y Circuitos 37