ESTADÍSTICA BÁSICA I Taller 2 ¿Porqué varían los resultados
Anuncio

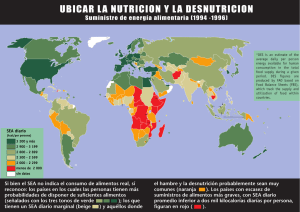
ESTADÍSTICA BÁSICA I 1. 2. 3. 4. 5. La estadística y sus objetivos Aplicación de la Estadística en Química Analítica Variabilidad analítica. Distribución normal Otros conceptos básicos. Intervalos de confianza Test de significancia: t-test Taller 2 Leonardo Merino NATIONAL FOOD ADMINISTRATION Science Department-Swedish National Food Agency Santiago de Chile, Julio 2013 ¿Porqué varían los resultados analíticos? • Por las incontrolables variaciones de las condiciones de operación (ej. Condiciones de repetibilidad y reproducibilidad) • Por las variaciones de las muestras (ej. inhomogeneidad de las muestras) Es muy importante saber diferenciar entre estas dos variaciones debido a que las acciones correctivas necesarias son muy diferentes. Estas dos variaciones están relacionadas a los dos fundamentales tipos de error analítico. (La estadística nos ayuda a distinguirlos de manera objetiva). NATIONAL FOOD ADMINISTRATION 1 Estadística Ciencia matemática que se ocupa de la variación de las muestras y la variación de los resultados de las mediciones. (La ciencia de inferir generalidades a partir de observaciones particulares). Objetivos de la Estadística Darnos un procedimiento lógico para sacar conclusiones en presencia de la incertidumbre de la medición. Se realiza al: • Resumir grupos de datos para describirlos de una manera concisa, clara y científica (Estadística descriptiva). • Establecer probabilidades de obtener ciertos resultados a partir de observaciones parciales (Estadística inferencial). (M. Thompson (2011). Notes on Statistics and Data Quality for Analytical Chemists) NATIONAL FOOD ADMINISTRATION Aplicación de la Estadística en Química Analítica • Cálculo de la variabilidad (precisión) y el sesgo • Identificación de diferencias estadísticamente significativas • Construcción, evaluación y uso de curvas de calibración • Cálculo de límites de detección y determinación • Cálculo de la incertidumbre de los valores medidos • Diseño de experimentos para el desarrollo de métodos y estudios de validación • Control estadístico del proceso de medición Los conceptos estadísticos son relevantes en todos las etapas de la experimentación comprendidos desde la planificación a la interpretación de los resultados. NATIONAL FOOD ADMINISTRATION 2 Estadística Clásica, Robusta y no-paramétrica µ-3 µ Estadística clásica es usada con datos que siguen una distribución normal. Se supone que los datos analíticos siguen esta distribución - Media y desviación estándar µ+3 Estadística robusta es usada con datos que siguen una distribución unimodal y simétrica pero con colas extendidas. Los datos analiticos siguen este comportamiento. - Media robusta y desviación estándar robusta Estadística no-paramétrica o de distribución libre no hace ninguna suposición sobre la distribución de los datos. - Mediana, MAD (Median Absolute Deviation) NATIONAL FOOD ADMINISTRATION Distribución normal p ( x ) 95% µ-2 µ ( x )2 2 2 µ+2 La distribución normal es definida por : NATIONAL FOOD ADMINISTRATION 1 e 2 = ubicación = dispersión Al aplicar la Estadística en química analítica se asume que el error analítico sigue la distribución normal. Se considera que el error total esta conformado por la combinación de un gran número de pequeños e independientes errores surgidos a lo largo de las varias etapas del procedimiento analítico (esto en un sistema analítico bien controlado). 3 Distribution Normal - Ubicación 1 La distribución puede ser caracterizada por su ubicación con el parámetro 0 NATIONAL FOOD ADMINISTRATION 1 2 nos permite distinguir entre diferentes distribuciones Distribution Normal - Dispersion 2 1 2 1= 2 1> 2 1 NATIONAL FOOD ADMINISTRATION El estadístico no es suficiente por si solo para caracterizar completamente una población. Otras distribuciones podrían estar localizadas en el mismo punto. Un segundo estadístico ( ), que mide la dispersión de la distribución, ayuda a diferenciarlas. 4 Caracterizando completamente una distribution normal = ubicación = dispersión NATIONAL FOOD ADMINISTRATION Distribución Normal – Propiedades importantes La curva es simétrica alrededor de µ. • Aproximadamente 68% de los datos se encuentran entre µ±1σ • Aproximadamente 95 % de los datos se encuentran entre µ±2σ • Aproximadamente 99.7 % de los datos se encuentran entre µ±3σ 68 % µ 95% 99.7% Nota: Un importante aspecto de esta distribución es que representa la probabilidad de que un simple resultado analítico esté dentro del rango definido por la curva normal. NATIONAL FOOD Lo contrario tambien se cumple, i.e., la probabilidad de que el valor verdadero puede ADMINISTRATION encontrarse dentro de un rango alrededor de nuestro simple resultado. 5 La media es calculada de la ecuación 0 n i 1 x n 1 i 1 xi 2 n x i = suma de resultados n = número de resultados El parámetro , define la ubicación de la distribución NATIONAL FOOD ADMINISTRATION Normalmente no se tiene acceso a la población total, sino sólo a un grupo n de datos, los cuales representan a la población. Por consiguiente, cuando calculamos la media de n resultados, estamos estimando la media de la población, . La media es representada por x Desviación estándar s n i 1 ( xi x )2 ( n 1 ) El estadístico , define la dispersión de la población La desviación estándar s es una medida de la dispersión de los resultados alrededor de la media. La desviación estándar está expresada en las mismas unidades que la media. NATIONAL FOOD ADMINISTRATION 6 Desviación estándar relativa (RSD) RSD s x Coeficiente de variación (CV) s CV % RSD 100 x NATIONAL FOOD ADMINISTRATION Cuando queremos comparar la dispersión de resultados que tienen diferente magnitud o unidades, la relación de la desviación estándar con respecto a la media puede ser de más utilidad que el solo valor absoluto de la dispersión. La varianza S2, es el cuadrado de la desviación estándar Varianzas son aditivas S2 = S12 + S22 +….+ Sn2 la varianza también describe la dispersión NATIONAL FOOD ADMINISTRATION Esta propiedad juega un rol de fundamental importancia en el análisis estadístico y tiene muchas aplicaciones, por ejemplo, errores provenientes de diferentes etapas en un procedimiento analítico pueden ser identificados y cuantificados. Asi, el analista está en la posibilidad de dirigir su atención a reducir sólo las fuentes de error significativas. 7 Desviación estándar de la media sM = Desviación estándar de la media, cuantifica la precisión de la media. Es decir, es una medida del intervalo en que podemos encontrar la media de la población. x n=1 n=3 x x NATIONAL FOOD ADMINISTRATION n = 19 x x x s SM n x S, cuantifica dispersión, i.e. que tanto varian los datos entre si. SM, cuantifica que tan exactamente se conoce la media de la población, i.e. la media de un número grande de muestras esta más cerca de la media poblacional que la media de un número pequeño de muestras. Intervalos de Confianza (IC) El Intervalo de Confianza de un resultado nos da el rango donde podríamos encontrar el “valor verdadero” de la media con una probabilidad determinada. El intervalo de confianza se calcula de la siguiente ecuación: IC x t (v, )s n t(, ) es el valor de t-students para grados de libertad y un nivel de significación de P () NATIONAL FOOD ADMINISTRATION Nota: Evite la confusión entre el nivel de significancia (P = ) y su complemento, el nivel de confianza (comunmente usado en las tablas estadísticas). 8 El Error (Analítico) Es definido como la diferencia entre un resultado individual y el “valor verdadero” de la medición. Es un valor simple. Tipos de errores Errores sistemáticos (veracidad,sesgo/recuperación), se dan cuando en el análisis repetido de una medición, el resultado permanece constante o varia de un manera previsible. Es independiente del número de mediciones y por lo tanto no disminuye con el aumento del número de análisis. Errores aleatorios (precisión, desviación estándar), se dan cuando los resultados individuales de una medición varían de un modo imprevisible. Este tipo de error no se puede compensar por corrección, sin embargo puede ser reducido con el aumento del número de observaciones. Errores espurios se dan típicamente como consecuencia de errores humanos o el malFOOD funcionamiento de los instrumentos. NATIONAL Eurochem/CITAC, 2012 ADMINISTRATION •Prueba de significancia 1: t-test NATIONAL FOOD ADMINISTRATION Evalua la evidencia dada por un dato, en favor de alguna afirmación hecha en relación a la población 9 Comparación de dos grupos de datos (A) ¿Son las medias diferentes? Las medias probablemente son iguales, es decir, pertenecen a la misma poblacion x1 x2 NATIONAL FOOD ADMINISTRATION Comparación de dos grupos de datos (B) ¿Son las medias diferentes? Las medias probablemente son diferentes, es decir, pertenecen a dos poblaciones diferentes x1 x2 La prueba de significancia nos ayuda a decidir objetivamente si la diferencia entre dos medias es real, o si ella proviene de variaciones aleatorias de la medición. La decisión no solo depende de la magnitud de las diferencias de las medias sino NATIONAL FOODde la cantidad de datos disponibles y de sus respectivas dispersión. tambien ADMINISTRATION 10 t-test (detectando errores sistemáticos) 1. Comparación de una media experimental con un valor conocido (one sample t-test) 2. Comparación de dos medias experimentales (two sample t-test) - Dos métodos analíticos (A y B) son usados repetidas veces en el análisis de una misma muestra. ¿Son los métodos diferentes? - Un método analítico es usado repetidas veces en el análisis de dos grupos de muestras (C y D). ¿Son las muestras diferentes? 3. Comparación entre pares de muestras (paired samples) NATIONAL FOOD ADMINISTRATION 1. Comparación de una media experimental con un valor de referencia Calcular el valor observado, tobs media Valor de referencia x tobs x s n Donde: S = desviación estándar de las mediciones n = número de mediciones = n-1 (grados de libertad) NATIONAL FOOD ADMINISTRATION Comprobar si hay un error sistemático en un método analítico, chequear la pureza de un material o si un valor critico (máximo límite) es excedido 11 2. Comparación de dos medias experimentales Calcular el valor observado, tobs media A t obs xA media B (x A xB ) scom nA1 nB1 2 s 2 n 1 sB2 nB 1 scom A A nA nB 2 xB Donde: scom = desviación estándar combinada = nA + nB - 2 (grados de libertad) NATIONAL FOOD ADMINISTRATION Esto es válido si las desviaciones estándares son similares (misma población) 3. Comparación entre pares de muestras (a) Muestra 6 A d5 5 d4 4 d3 3 2 1 Distinguiendo y separando dos fuentes de variación B d6 d2 d1 Resultados Muestra 6 5 d6 = B-A d5 4 3 d4 d3 2 d2 1 NATIONAL FOOD ADMINISTRATION d1 0 d Diferencias 12 3. Comparación entre pares de muestras (b) Calcular el valor observado, tobs t obs d S d n Donde: d = la media de las diferencias de resultados Sd = desviación estándar de las diferencias n = número de diferencias de pares = n-1 (grados de libertad) Nota: El rango de variación entre las concentraciones de los diferentes pares de muestras debe ser restringido. NATIONAL FOOD ADMINISTRATION Hallando el valor crítico (tcrit) • Calcular los grados de libertad (1 ) • Elegir la probabilidad (usualmente 95% o P=0.05) • Usar las tablas estadísticas (para el correcto número de colas) • Comparar: Si tobs > tCrit hay diferencia estadísticamente significativa NATIONAL FOOD ADMINISTRATION Observar que aun cuando el análisis estadístico puede detectar una “significancia estadística” esto puede no tener una significación química de importancia práctica. El criterio de importancia práctica proviene de una fuente externa independiente, no de los resultados. 13 Una cola ¿Una o dos-colas ? Ej: Cuando se quiere saber si un límite de especificación es excedido o no Ejemplo, un límite máximo de un contaminante (ML) tcrit Dos-colas Ej: Queremos saber, si el valor medido esta dentro de un rango establecido 95 % NATIONAL FOOD ADMINISTRATION tcrit Ejemplo, uso de un material de referencia Total 5% Prueba de significancia: Método clásico Prueba de una-cola o de dos-colas 1. “La media es igual al valor dado” vs “la media no es igual al valor dado” ( = x0) ( x0) dos-colas 2. “La media es igual al valor dado” vs “la media es menor que el valor dado” ( = x0) ( < x0) una-cola 3. “La media es igual al valor dado” vs “la media es mayor que el valor dado” ( = x0) ( > x0) una-cola Al hacer una prueba de significancia se comprueba la veracidad de una hipótesis experimental, llamada “hipótesis alternativa” (HA, si hay diferencia,) con respecto a la hipótesis nula (H0, no hay diferencia). Es la hipótesis alternativa la que determina el número de colas. NATIONAL FOOD ADMINISTRATION Si la hipótesis alternativa contiene la frase “mayor que” ó “menor que”, la prueba es de una-cola. Si la hipótesis alternativa contiene la frase ”no es igual que”, la prueba es de dos-colas. 14 Valores Críticos para la distribución t : Una cola: 0.25 (75%) 0.10 (90%) 0.05 (95%) 0.025 (97.5%) 0.01 (99%) 0.005 (99.5%) : Dos colas: 0.50 (50%) 0.20 (80%) 0.10 (90%) 0.05 (95%) 0.02 (98%) 0.01 (99%) 1 1.000 3.078 6.314 12.706 31.821 63.657 2 0.816 1.886 2.920 4.303 6.965 9.925 3 0.765 1.638 2.353 3.182 4.541 5.841 4 0.741 1.533 2.132 2.776 3.747 4.604 5 0.727 1.476 2.015 2.571 3.365 4.032 6 0.718 1.440 1.943 2.447 3.143 3.707 7 0.711 1.415 1.895 2.365 2.998 3.499 8 0.706 1.397 1.860 2.306 2.896 3.355 9 0.703 1.383 1.833 2.262 2.821 3.250 10 0.700 1.372 1.812 2.228 2.764 3.169 11 0.697 1.363 1.796 2.201 2.718 3.106 12 0.695 1.356 1.782 2.179 2.681 3.055 13 0.694 1.350 1.771 2.160 2.650 3.012 14 0.692 1.345 1.761 2.145 2.624 2.977 15 0.691 1.341 1.753 2.131 2.602 2.947 Grados de libertad: NATIONAL FOOD ADMINISTRATION http://www.microbiologybytes.com/maths/t.html Interpretación del t-test Si al aplicar el test de significancia encontramos que: tcrit > tobs Podemos afirmar lo siguiente: • no hay diferencia estadísticamente significativa • no hay error sistemático medible (bajo las condiciones experimentales) • Pero NO podemos afirmar que: No existe error sistemático (puede haber un error sistemático no detectado) NATIONAL FOOD ADMINISTRATION 15 Secuencia de aplicación de una prueba de significancia • Formular la pregunta (¿error sistemático o aleatorio?) • Seleccionar el tipo de prueba (¿t-test? ¿F-Test?) • Calcular el estadístico observado (tobs o Fobs) • Calcular los grados de libertad () • Elegir el nivel de confianza (generalmente 95%, =0.05) • Decidir el número de colas (¿una-cola ? ¿dos-colas ?) • Buscar en las tablas el valor crítico del estadístico (tcrit o Fcrit) • Comparar ambos valores y tomar la decisión estadística NATIONAL FOOD ADMINISTRATION p-value: Método moderno de la prueba de significancia Un p-value es una medida de la evidencia que se tiene en contra de la hipotesis nula. La hipotesis nula (Ho) es la hipótesis de no-cambio o no-efecto. Alta probabilidad (P cercanos a 1) Baja probabilidad (P < 0.05) p-value > 0.05 = no significancia (aceptamos la Ho) p-value < 0.05 = si hay significancia (rechazamos la Ho) 95% En análisis químico se acostumbra afirmar que p-value ≤ 0.05 son estadísticamente significantes. µ NATIONAL FOOD ADMINISTRATION x Las áreas rojas muestras la probabilidad de que la hipótesis nula es verdadera. 16 Activando las funciones estadísticas en Excel (97-2003) • En el Menu marcar Tools, marcar Add-Ins... (1), marcar Analysis Toolpak (2) • En el Menú tool se puede ver ahora Data analysis...(3) 2. 1. 3. NATIONAL FOOD ADMINISTRATION t-test en EXCEL (Versión 97-2003) 3. 2. 1. 4. NATIONAL FOOD ADMINISTRATION 17 Recordar que: Hemos visto 3 tipos de aplicaciones del t-test: Comparación de una media con un valor (one sample t-test) Comparación de dos medias (two samples t-test) Comparación entre pares de muestras (paired samples) y dos alternativas de colas para usar las tablas estadísticas: Una-cola Dos-colas Por lo tanto, se tiene seis combinaciones, cinco son equivocadas y sólo una es la correcta. NATIONAL FOOD ADMINISTRATION Taller 2 Usando las notas del curso y una calculadora (si es necesario), identifique el tipo de variación que corresponde en cada uno de los casos dados y el tipo de t-test que debe aplicarse. Referencias • Miller, J.N. & Miller, J.C. Estadística y Quimiometría para Química Analítica. Prentice Hall. 4ta Ed. 2000 • Method validation Course 0072. LGC limited. London 2002 • Morgan, E. Chemometrics. Experimental Design. John Wiley & Sons, London 1991 • Thompson, M. The Frequency Distribution of Analytical Error, Analyst, (1980) Vol. 105 • Thompson, M & Lowthian, P. (2011) Notes on Statistics and Data Quality for Analytical Chemists. Imperial college Press, London • VAMSTAT II. Statistic Training for Valid Analytical Measurement. VAM. LGC Teddington Ltd. 1996-2000 NATIONAL FOOD ADMINISTRATION 18