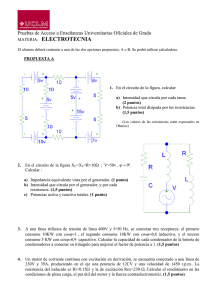
corriente continua - IES María Zambrano

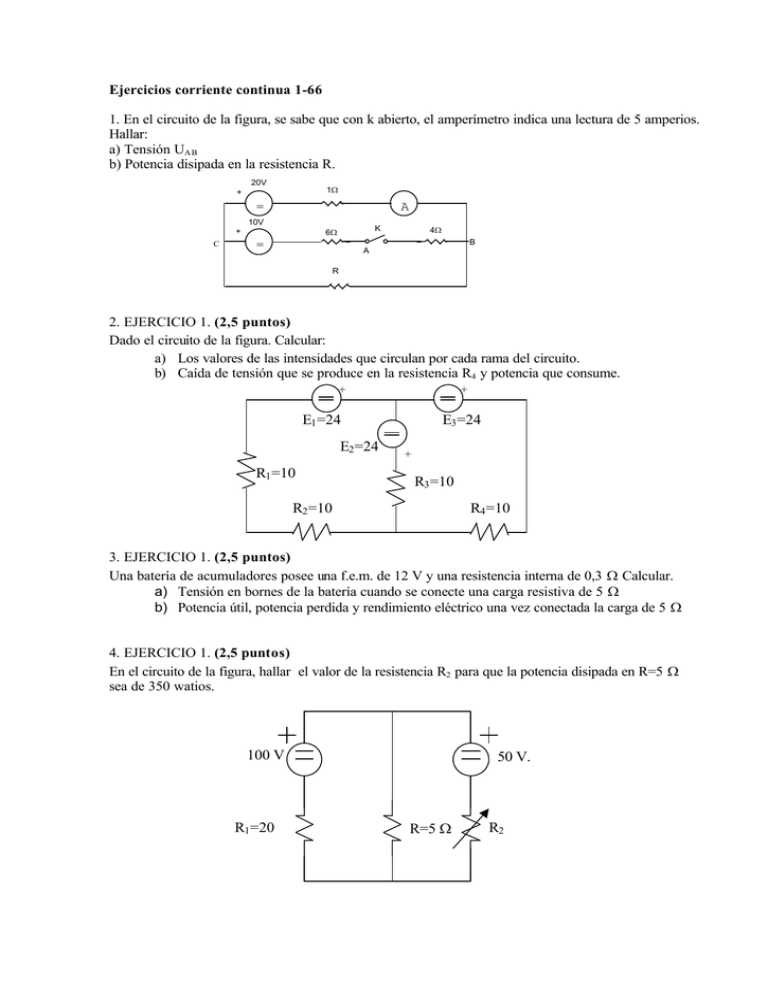
Ejercicios corriente continua 1-66
1. En el circuito de la figura, se sabe que con k abierto, el amperímetro indica una lectura de 5 amperios.
Hallar:
a) Tensión UAB
b) Potencia disipada en la resistencia R.
20V
+
1Ω
=
A
10V
+
C
K
6Ω
4Ω
B
=
A
R
2. EJERCICIO 1. (2,5 puntos)
Dado el circuito de la figura. Calcular:
a) Los valores de las intensidades que circulan por cada rama del circuito.
b) Caída de tensión que se produce en la resistencia R4 y potencia que consume.
+
+
E1 =24
V
E2 =24
V
E3 =24
V
R1 =10
Ω
R2 =10
Ω
+
R3 =10
Ω
R4 =10
Ω
3. EJERCICIO 1. (2,5 puntos)
Una batería de acumuladores posee una f.e.m. de 12 V y una resistencia interna de 0,3 Ω Calcular.
a) Tensión en bornes de la batería cuando se conecte una carga resistiva de 5 Ω
b) Potencia útil, potencia perdida y rendimiento eléctrico una vez conectada la carga de 5 Ω
4. EJERCICIO 1. (2,5 puntos)
En el circuito de la figura, hallar el valor de la resistencia R2 para que la potencia disipada en R=5 Ω
sea de 350 watios.
100 V
v.
R1 =20
50 V.
R=5 Ω
R2
5. EJERCICIO 1. (2,5 puntos)
Cuatro pilas iguales de 1,5 Voltios de f.e.m , y 0,1 Ohmios de resistencia interna cada una , se
asocian en serie y se conectan a una resistencia exterior de carga, comprobándose que por ella circula
una corriente de 6 Amperios de intensidad. Si dichas pilas se asocian en paralelo y se conectan a la
misma resistencia anterior , ¿ Que intensidad circulará por ella ?.
6. EJERCICIO 1. (2,5 puntos)
En el circuito de la figura calcular:
a) Intensidad de la corriente en cada rama
b) La tensión en la resistencia de 2 ohmios
c) La potencia disipada en la resistencia de 5 Ω
7. EJERCICIO 1. (2,5 puntos)
Entre las características técnicas de un televisor podemos leer 200 voltios, 400 watios. Calcula:
a) Intensidad de corriente que circula por el receptor.
b) Su resistencia
c) El precio que cuesta mantenerlo en funcionamiento 8 horas si el Kwh cuesta 15 Ptas.
d) El calor generado si el rendimiento es del 95 %
8. EJERCICIO 1. (2,5 puntos)
Se tiene el sistema formado por dos resistencias en paralelo de 5 Ω y 10 Ω respectivamente conectado
en serie con una resistencia de 15 Ω. El sistema anterior se conecta a una batería de 220 V. Calcular:
a) Caída de tensión en cada una de las resistencias.
b) Intensidades que circulan por cada una de las resistencias.
c) Potencia en cada una de las resistencias.
9. EJERCICIO 1. (2,5 puntos)
Un radiador eléctrico lleva la siguiente inscripción que dice: 220 Voltios (V) , 1760 Vatios
(W).
Calcular:
a) La intensidad de la corriente que circula por él.
b) Su resistencia.
c) El coste del consumo en 2 horas, sabiendo que el Kw.h , cuesta 20 pts.
d) El número de calorías que desprende en esas 2 horas , suponiendo que toda la energía
eléctrica se transforma en calor
10. EJERCICIO 1. (2,5 puntos)
Hallar el valor que ha de tener la fuerza electromotriz, ε del generador intercalado en el circuito de la
figura, para que el potencial del punto A sea 9 voltios.
11. EJERCICIO 1. (2,5 puntos)
Un generador tiene una tensión de 8’7 voltios a circuito abierto, y de 8 voltios cuando suministra una
corriente de 12 amperios. Calcular:
a) Resistencia interior del generador.
b) Fuerza electromotriz del generador.
c) Potencia útil.
d) Potencia total.
e) Rendimiento.
12. EJERCICIO 1. (2,5 puntos)
Dos calefactores eléctricos de 1000 W/ 220 V cada uno se conectan en serie a una red de 220 V.
Calcular:
a) Intensidad que circula por el circuito.
b) Potencia total del conjunto.
13. EJERCICIO 1. (2,5 puntos)
Dado el circuito eléctrico de la figura encontrar los valores siguientes:
a) Valor de Ia, Ib, V0.
b) Potencia disipada por cada resistencia.
c) Potencia que suministra la fuente de 200 voltios.
14. EJERCICIO 3. (2,5 puntos)
El siguiente esquema funcional, refleja la instalación eléctrica de un radiador que posee un conmutador
de 3 posiciones para regular la potencia calorífica. Calcular el valor de cada una de las resistencias si se
sabe que el consumo del radiador al situar el conmutador en:
a) La posición 1 es de 1 kW-h.
b) La posición 2 es de 2 kW-h.
c) Laposición3 es de 3 kW-h.
15. EJERCICIO 1. (2,5 puntos)
En el circuito eléctrico de la figura, la intensidad Io= 1 A. Calcular:
a) Intensidad I1
b) Potencia disipada en cada resistencia
c) Comprobar que la potencia total que disipa el circuito es la potencia generada por la fuente de 150V
16. EJERCICIO 1. (2,5 puntos)
Dado el circuito de la figura, hallar:
a) El valor de la intensidad total (I) que circula, para que la diferencia de potencial entre A y B sea el
doble de la caída de tensión en la resistencia R1
b) En las mismas condiciones anteriores, determinar los valores de R2 y R3 para que la intensidad que
circula por R3, sea doble que la intensidad que circula por R2.
17. EJERCICIO 1. (2,5 puntos)
Uniendo mediante una resistencia de 7 ohmios los terminales de una batería de E=5 V de fuerza
electromotriz y resistencia interna r, circula una corriente de 0,5 A. Hallar:
a) Resistencia interna de la batería.
b) Potencia eléctrica generada por la fuerza electromotriz E.
c) Potencia absorbida por la resistencia exterior.
d) Potencia perdida en la batería.
18. EJERCICIO 1. (2,5 puntos)
En el circuito de la figura, calcular la intensidad de la corriente que circula por las resistencias A y B.
19. EJERCICIO 1. (2,5 puntos)
Las corrientes Ia e Ib del circuito eléctrico de la figura valen 4 A y -2 A respectivamente. Determinar:
a) Intensidad IG.
b) Potencia disipada por cada resistencia.
c) Fuerza electromotriz EG.
d) Comprobar que la potencia que suministra la fuente de fuerza electromotriz EG es igual a la potencia
que consumen los demás elementos.
20. EJERCICIO 2. (2,5 puntos)
Dado el circuito de la figura, calcular:
a) Intensidad a través de la resistencia R4=4 ohmios cuando el interruptor K está abierto.
b) Intensidad a través de la resistencia R4=4 ohmios cuando el interruptor K está cerrado.
c) Potencia disipada en la resistencia R1=2 ohmios cuando K está cerrado.
21. EJERCICIO 1. (2,5 puntos)
Si la resistencia R del circuito de la figura disipa una potencia 10 veces superior a la de la resistencia de
10 ohmios, determinar:
a) Intensidad que circula por R.
b) Diferencia de potencial (d.d.p.) existente en R.
c) Potencia disipada por R.
22. EJERCICIO 1. (2,5 puntos)
Hallar la potencia disipada por la resistencia de 3 ohmios , representada en la figura.
23. EJERCICIO 1. (2,5 puntos)
Un alumno desea medir la corriente que circula por la resistencia R, del circuito de la figura, con un
amperímetro.
a) Por error conecta el amperímetro en paralelo con la resistencia R, ¿cuánto marcaría el amperímetro?.
b) Se da cuenta de su error y vuelve a conectar al circuito el amperímetro, pero esta vez en serie, tal
como se muestra en la figura, ¿cuál será la lectura en estas condiciones?.
24. EJERCICIO 1. (2,5 puntos)
En el circuito de la figura determinar:
a) Intensidad del circuito.
b)Tensiones VAB (VA - VB) , VBC y VCA.
25. EJERCICIO 3. (2,5 puntos)
Una batería de un automóvil (fuente real), posee entre sus terminales una tensión a circuito abierto de
12,6 V, siendo la intensidad cuando se cortocircuitan dichos terminales de 300 A. Determinar la
potencia que proporciona dicha batería cuando en sus terminales, se conecta una resistencia de 1 ohmio.
26. EJERCICIO 1. (2,5 puntos)
Dado el circuito de la figura ( siendo R1=2 ohmios ; R2=3 ohmios ; R3=4 ohmios y R4=6 ohmios ),
hallar:
a) Las intensidades de cada rama
b) La tensión, VCD
d) La tensión de alimentación, VAB
27. Determinar la tensión V que se aplica a un receptor alimentado por una línea eléctrica de 1 mm2 de
sección y 50 m de longitud por la que circula una corriente de 5 A y una tensión de 230 V en el punto de
conexión. (Resistividad del cobre r=1,7x10ª Wxm).
28. Cuestión 1ª:
En el circuito de la figura l, las cuatro resistencias son iguales. La encerrada en el círculo consume 10W.
Halla la potencia que consume el conjunto.
29. Cuestión 1ª:
En el circuito de la figura l, las cuatro resistencias son iguales. La encerrada en el círculo consume 10W.
Halla la potencia que consume el conjunto.
30. En el circuito de la figura hallar:
a.- La expresión de la tensión en el nudo A.
b.- La expresión de la potencia suministrada por la fuente de f.e.m. 2E.
(Puntuación máxima 2,5 puntos)
31. Ejercicio 2
La resistencia equivalente correspondiente a la asociación de tres resistencias iguales conectadas en
serie es de 75 W, y la intensidad que circula por cada una de ellas es de 1,5 A. Calcular:
a.- Cuánto valdrá cada una de las resistencias.
b.- Caída de tensión que se produce en la resistencia equivalente cuándo se conectan las tres en
serie.
c.- Potencia consumida.
d.- Caída de tensión que se produce en cada una de las tres resistencias conectadas en serie.
e.- Cuánto valdrá la resistencia equivalentes¡ conectamos en paralelo las tres resistencias.
Dibuja el esquema correspondiente.
(Puntuación máxima 2,5 puntos)
32. CUESTIÓN 1ª (5 puntos)
Dado un receptor con una fuerza contraelectromotriz Eª (voltios) y resistencia interna r (ohmios),
conectado a una red de V (voltios) y por el que circula una intensidad de l (amperios), dibuja un
esquema del circuito y deduce:
a.
b.
c.
d.
La ecuacón de tensiones para ese receptor.
La ecuacón de potencias.
La ecuacón de energías.
Demostrar que el rendimiento es h<I.
33. CUESTIÓN 1ª (5 puntos)
En el circuito de la figura 4, hallar el potencial del punto A, cuando:
a. El interruptor K está abierto.
b. El interruptor K está cerrado.
c. ¿Qué intensidad circulará con k cerrado por cada una de las resistencias de R (ohmios).
34. Cuestión 1ª.
Se tienen dos fuentes reales, de f.e.m. "E" voltios y resistencia interna "r" y "2r" ohmios
respectivamente. Si cada una alimenta a un receptor de valor R ohmios, halla la relación entre las
potencias P1 y P2 disipadas en la resistencia interna de cada fuente.
35. Cuestión 2ª.
Una lámpara de incandescencia, puede considerarse como una resistencia óhmicamente pura. Sus
valores nominales de tensión y potencia son 220 V y 60 W respectivamente.
a. ¿Qué intensidad circula por el filamento cuando la lámpara se conecta a una red de 220 V?,
¿cuál es, entonces, la resistencia del filamento incandescente?.
b. Si conectamos la lámpara a una red de 380 V, ¿qué resistencia es preciso intercalar para que la
lámpara funcione en las mismas condiciones que en el caso anterior?.
c. La resistencia que se intercala está construida con hilo metálico de 0,2 mm de diámetro, cuya
resistividad es de 0,46 Wmm2 /m. ¿Cuál será la longitud de este hilo?.
d. Si el kW-h vale 18 ptas (I.V.A. incluido), ¿cuál es el gasto correspondiente a diez horas de
funcionamiento de la lámpara, a 220 V?.
36. En el circuito de la figura, teniendo en cuenta los valores indicados y aplicando el teorema de
superposición, calcular:
a.- El valor de la corriente IAB que circula por la resistencia R2.
b.- El valor que debería tener la fuente E2 para conseguir que no pase corriente por la resistencia
R2
(Puntuación máxima 2,5 puntos)
37. PROBLEMA (5 puntos)
Se tiene una estufa eléctrica de 500 W conectada, durante 30 minutos, a una tensón de 220 voltios
mediante un conductor de cobre de 5 m de longitud y 1,5 mm2 de seccón. Calcular las pérdidas de
potencia en el conductor y la energía consumida en la estufa. (Resistividad del cobre 1,7 l0ªohmiosxm).
38. PROBLEMA (5 puntos)
Aplicando el teorema de superposición, calcular la intensidad de corriente que circulará por la rama A-B
de la figura 5.
39. Cuestión 2ª.
Un coche de juguete está alimentado por una pila de 9 V de f.e.m. y 10 de resistencia interna. Con un
voltímetro podemos observar que si impedimos el giro del motor, marca 8,4 V, y cuando gira con
normalidad marca 8,8 V Calcula:
a. La resistencia interna del motor.
b. La fuerza contraelectromotriz.
40. Aplicación.
¿Cuantas baterías de 12 V, 50 Ah serán necesarias y cómo se tendrían que conectar para alimentar un
calefactor durante 20 horas, si se sabe que conectado a su tensión nominal 24 V, circula una corriente de
5A?.
41. Ejercicio 2
Una bombilla de 120V. y 60 W se conecta en paralelo con una resistencia de 80 ohmios. ¿Qué
resistencia mínima debe ponerse en serie con el conjunto para que conectado a 220 V, no se funda la
bombilla?
(Puntuación máxima 2,5 puntos)
42. Cuestión 2?.
Una batería de generadores tiene una tensión de 12 V a circuito abierto y de 11,2 V cuando se conecta a
un circuito al que suministra 5 A. Calcula:
a.
b.
c.
d.
Resistencia interna de la bater
Potencia ?cuando suministra 5 A.
Potencia suministrada por la fuente.
Rendimiento.
43. Ejercicio 2
Dado el circuito de la figura, calcular:
a) El valor de VRD, cuando las resistencias tienen el valor indicado.
b) El valor que debe tener R3 , para que sin cambiar las demás resistencias, el valor de VRD, sea cero
voltios.
44. Ejercicio 2
Dado el circuito de la figura, calcular:
a) El valor de VBD, cuando las resistencias tienen el valor indicado.
b) El valor que debe tener R3 , para que sin cambiar las demás resistencias, el valor de VBD, sea cero
voltios.
45. Ejercicio 4
Explica razonadamente el funcionamiento de un generador de corriente continua en vacío y en carga.
(Puntuación máxima 2,5 puntos)
46. CUESTIÓN 2ª (5 puntos)
Define los conceptos de intensidad de corriente eléctrica y densidad de corriente. Explica los principales
efectos de la corriente eléctrica.
47. Problema.
Una máquina cortacésped eléctrica está dotada de un motor de corriente continua de 220 V, absorbiendo
una corriente de 2,5A. La distancia desde el generador al receptor es de 20 m. Admitiendo una densidad
de corriente de 3 A/mm2 y una resistencia específica de 0,018 S2•mm2 /m, calcular:
a. Diámetro (en mm) del conductor.
b. La caída de tensión en el conductor de conexión.
c. El valor de la energía eléctrica consumida por la máquina al cabo de 90 minutos de
funcionamiento, sabiendo que el precio del kilovatio-hora es de 14 ptas.
48. Ejercicio 2
Dado el circuito de la figura, se pide calcular:
a.- Lectura del amperímetro A conectado en el circuito.
b.- Lectura del voltímetro V conectado en el circuito.
49. Ejercicio 2
Una dinamo de fuerza electromotriz 100V y resistencia interna 312 se conecta en serie a una
resistencia de 20 92 v a un motor de fuerza contraelectromotriz 50 V y resistencia interna 2 U.
Calcular
a.- Intensidad de corriente en el momento de arranque del motor.
b.- Intensidad de corriente durante el normal funcionamiento del motor.
c.- Potencia total del generador.
d.- Potencia útil del motor despreciando las pérdidas mecánicas.
e.- Tensión en los bornes del generador y del motor.
(Puntuación máxima 2,5 puntos)
50. Ejercicio 2
En el circuito de la figura, el voltímetro marca 25 V cuando el interruptor k está abierto.
a.- En estas condiciones hallar la f.e.m. E3 si VA < VB.
b.- Hallar la potencia suministrada por la fuente E3 .
c.- Si se cierra el interruptor k, hallar la potencia suministrada o consumida por la fuente E3
51. Ejercicio 2
Una resistencia eléctrica se conecta a una fuente de tensión de 240V. Si consume cada 30 horas de
funcionamiento 75 kWh, se pide calcular:
a.- Energía que consume la resistencia en julios.
b.- Potencia de la resistencia.
c.- Intensidad que recorre la resistencia.
d.- Valor de la resistencia.
(Puntuación máxima 2,5 puntos)
52. Ejercicio 3
Calcular el coste por hora que supone la utilización de un radiador eléctrico para el calentamiento
continuo de una habitación, suponiendo que se necesitan 40 kcal por hora y por m3 . La habitación
tiene una planta de 5 m x 4 m y una altura de 3 m. Considerar que la energía eléctrica cuesta 15 pts
por kWh. Si la resistencia del radiador tiene un valor de 5 ohmios ¿cuál será la intensidad consumida
por el mismo?
(Puntuación máxima 2,5 puntos)
De otras comunidades
53. (MURCIA) P1) En el circuito mostrado en la figura las fuentes de tensión son de
continua y el circuito se encuentra en régimen permanente. Para este circuito
determine:
a) Nº de mallas del circuito y ecuaciones de las mismas. (0.8 p)
b) Determine las intensidades que circulan por cada uno de los elementos pasivos y activos del circuito.
(1.4 p)
c) Potencia generada o absorbida -indicando claramente este punto- por las fuentes de tensión. (0.8 p)
54. P1) En el circuito mostrado en la figura las fuentes de tensión son de continua y el circuito se
encuentra en régimen permanente. En estas condiciones determine:
a) Nº de mallas del circuito y ecuaciones de las mismas -sólo escritura de las ecuaciones, sin resolución
de las mismas-. (1.0P)
b) Determine el equivalente de Thevenin del circuito a la izquierda de los terminales A y B. (1.2p)
c) Utilizando el equivalente obtenido en el apartado b) ¿cuál tendría que ser el valor óhmico de la
resistencia R, para que la potencia cedida a esta resistencia sea máxima? (0.8p)
55. C3) Determina para el circuito mostrado en la figura:
a) Equivalente de Thevenin del mismo desde los terminales A y B -a la izquierda de los mismos. (1.0p)
b) Equivalente de Norton visto desde los terminales A y C. (1.0P)
56. P1) Para el circuito eléctrico de la figura, cuyas fuentes son de continua, se desea determinar,
supuesto régimen de funcionamiento estacionario:
a) Número de mallas del circuito y ecuaciones de las mismas. (1.0P)
b) Intensidades en las resistencias. (1.0p)
c) Potencias generadas o consumidas por las fuentes de tensión. (1.0p)
57. C3) Dado el circuito mostrado en la figura inferior izda., determina entre A y B:
a) La intensidad de cortocircuito. (0.7 p)
b) La tensión de vacío (0.7 p)
c) La impedancia de entrada o equivalente. (0.6 p)
58. C4) Con los datos que se proporcionan en la figura superior derecha, determina:
a) Tensión en cada elemento del circuito. (1.0 p)
b) Potencia consumida o generada por cada elemento. (1.0 p)
59. P1) Para el circuito eléctrico de la figura, cuyas fuentes son de continua, se desea
determinar -supuesto régimen de funcionamiento estacionario-:
a) Número de mallas del circuito y ecuaciones de las mismas. (1.0 p)
b) Intensidades en las resistencias de 5 y
. (1.0 p)
c) Potencias generadas o consumidas por las fuentes de tensión. (1.0 p)
60.
61.
62. C3) Dado el circuito mostrado en la figura inferior izda., determine entre A y B:
a) La intensidad de cortocircuito. (0.7 p)
b) La tensión de vacío. (0.7 p)
c) La impedancia de entrada o equivalente. (0.6 p)
63. C3) Dado el circuito mostrado en la figura inferior izda., determine entre A y B:
a) La intensidad de cortocircuito.
b) La tensión de vacío.
64. Pl) Para el circuito eléctrico de la figura, cuyas fuentes son de continua, se desea determina –
supuesto régimen de funcionamiento estacionario-:
a) Número de mallas del circuito y ecuaciones de las mismas. (1.2 p)
b) Valor de la fuente E, para que la potencia absorbida en la resistencia de 7 ohmios sea de 28W. ( 1.8 p
)
65. P1) Para el circuito eléctrico en continua de la figura, se desea determinar, supuesta la resistencia
Rx= W:
a) Equivalente de Thevenin del circuito visto desde los terminales A y B. (1.0 p)
b) Intensidad de cortocircuito entre A y B. (0.6 p)
c) Equivalente de Norton -equivalente en forma de fuente de intensidad e impedancia - del circuito visto
desde los terminales A y B. (0.6 p)
d) Valor que debería tener la resistencia R,, para que la tensión entre los terminales A y B sea nula.(0.8
p)
66. P1) Para el circuito eléctrico en continua de la figura, se desea determinar, supuesto régimen
estacionario:
a) Número de mallas del circuito y ecuaciones de las mismas. (1.0P)
b) Tensión el la resistencia de 10 0. (0.5p)
e) Potencias consumidas en las resistencias de 2 y 10 9. (0.5p)
d) Potencias generadas y consumidas por las fuentes de tensión. (1.0P)