3.- Programación por metas.
Anuncio

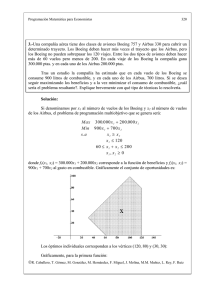
Programación Matemática para Economistas 1 3.- Programación por metas. Una vez mencionados algunos de los inconvenientes de las técnicas generadoras, la incorporación de información se va a traducir en una acción del decisor o centro decisor, emitiendo “deseos” al analista y éste, en base a estos deseos va a actuar. De esta manera, renunciamos a la optimización pero obtenemos una solución que satisface los deseos manifestados. La técnica que se emplea al incorporar información a priori en el proceso se denomina, Goal Programming, o Programación por Metas. Veamos en qué consiste. Dado un problema general de programación multiobjetivo: Opt ( f 1 (x), f 2 (x),L , f p (x)) s. a x ∈ X donde algunos de los objetivos serán de máximo y otros de mínimo, el decisor actúa de la siguiente forma: Primero asignará a cada uno de los objetivos un valor ui que va a representar su nivel de aspiración, es decir, lo que desea alcanzar como mínimo o bien no desea superar, e incluso, en algunos casos, desea alcanzar exactamente la igualdad, para el correspondiente objetivo. Después, al conjugar el objetivo y el nivel de aspiración se obtiene lo que denominamos meta, que expresamos de la siguiente forma: Si estamos maximizando fi(x) al imponer un nivel ui, se deseará que: fi(x) ≥ ui. Si minimizamos, se deseará que fi(x) ≤ ui. El caso de igualdad, fi(x) = ui, se puede contemplar tanto si maximizamos como si minimizamos. Posteriormente al establecimiento de las metas, se asignan niveles de prioridad entre los objetivos, es decir, se les ordena atendiendo a las prioridades que manifieste el decisor. Esta asignación puede ser uno a uno, es decir, en cada nivel un solo objetivo, o pueden aparecer varios compartiendo un mismo nivel; este caso implica una ponderación entre los objetivos que comparten el nivel. El número de niveles de prioridades será por tanto, s ≤ p. Así pues, la resolución se llevará a cabo atendiendo a las metas impuestas y a los niveles de prioridad establecidos, de forma que se preferirá una solución que mejore al primero, una vez conseguida, se pasa al segundo y así sucesivamente. En este sentido, la ordenación que se utiliza, bajo el enfoque de programación por metas, es la lexicográfica R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 2 llevándose a cabo una resolución por niveles. Esto nos conduce a definir un nuevo orden denominado lexicográfico, el cual pasamos a definir. Orden Lexicográfico: Diremos que un punto x es preferido a x’ si se verifica que: fi(x) = fi(x’) ∀ i = 1, ..., j - 1 y fj(x) > fj(x’). El orden lexicográfico es un orden total y es el usado en la ordenación del diccionario. Con él se establece que para mejorar una combinación basta con ir mejorando sucesivamente las coordenadas sin tener en cuenta lo que ocurra con las restantes. A las soluciones obtenidas por la técnica de programación por metas se las denomina satisfactorias, en el sentido de que verifican evidentemente las restricciones originales del problema y las metas impuestas por el centro decisor. Así pues tenemos. Definición 4. Un punto x* es una solución satisfactoria si es admisible, y verifica las p-metas impuestas, es decir: x* ∈ X max f i (x* ) ≥ ui min f i (x* ) ≤ ui max min f (x* ) = u i i En estas condiciones, es decir, una vez que el decisor ha manifestado sus niveles de aspiración, construidas las metas y priorizados los objetivos, para la resolución y aplicación de la técnica de programación por metas se introducen en las metas del problema unas variables (positivas) denominadas de desviación, y denotadas por n, y p. Dichas variables nos van a representar las diferencias que existen entre los niveles de aspiración impuestos por el decisor y el resultado que se alcanza en cada objetivo. La introducción se realiza de la siguiente forma: Si estamos maximizando fi(x) al construir las metas tenemos: fi(x) ≥ ui entonces fi(x) + ni - pi = ui y Min ni. ¿Por qué? Porque, si ni = 0 entonces fi(x) - pi = ui y se verifica la meta fi(x) ≥ ui. Si estamos minimizamos fi(x) al construir la meta tenemos: fi(x) ≤ ui entonces fi(x) + ni - pi = ui y Min pi R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 3 razonando de igual forma, si pi = 0 entonces fi(x) + ni = ui y por tanto se cumple la meta fi(x) ≤ ui. En el caso de igualdad, fi(x) = ui, se toma fi(x) + ni - pi = ui y se calcula Min ni + pi, para que se mantenga la meta se tendrá que verificar que ni = pi = 0. A la función que recoge la minimización de la variable no deseada, en el sentido de que queremos que sea nula, se le denomina función de realización o función logro, y las denotaremos por hi(n, p). Así pues, dadas las metas, los niveles de prioridad y determinadas las funciones de realización, se procede a calcular: lexmin (h1 (n, p), L , hs (n, p)) s. a x ∈ X f i (x) + ni − pi = ui i = 1,..., p ni , pi ≥ 0 En general, al primer conjunto de restricciones, que son las originales del problema se les denomina restricciones duras o técnicas, debido a que serán restricciones que se tienen que verificar necesariamente. Al segundo conjunto de restricciones, que son las que se generan de la construcción de las metas, se les denomina restricciones blandas, debido a que no son de obligado cumplimiento. En cualquier problema, una vez planteado, y antes de proceder a la resolución lexicográfica, se lleva a cabo la comprobación, de la existencia de puntos factibles, es decir, que nuestro conjunto de restricciones duras no es vacío, dado que si lo fuera el problema no tendría ningún sentido. Esta comprobación se realiza en el que denominaremos Nivel 0, en el cual minimizamos cualquier función constante sujeta a las restricciones duras del problema. Nivel 0: M in h ( x ) = cte s. a x∈ X Una vez comprobado que existen soluciones factibles, se pasa a la resolución del problema. Para mostrar todo lo comentado vamos a desarrollar un ejemplo teórico. Supongamos que nuestro problema esta definido de la siguiente forma: ( Max f 1 , s. a Min f 2 , x∈ X Max f 3 , Min f 4 ) R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 4 por tanto, tenemos un problema de cuatro objetivos, donde dos de ellos corresponden a máximos y dos a mínimos. El siguiente paso es dar los niveles de aspiración, construir las metas y determinar la variable no deseada, para la determinación de la correspondiente función de realización o logro. Sea pues: f1(x) ≥ u1 entonces f1(x) + n1 - p1 = u1 y Min n1 f2(x) ≤ u2 entonces f2(x) + n2 - p2 = u2 y Min p2 f3(x) ≥ u3 entonces f3(x) + n3 - p3 = u3 y Min n3 f4(x) = u4 entonces f4(x) + n4 - p4 = u4 y Min n4 + p4. Vamos a considerar que los niveles de aspiración se establecen como: Nivel 1: Objetivo 1, entonces la función de realización es: h(n1, p1) = n1 Nivel 2: Objetivo 2, entonces la función de realización es: h(n2, p2) = p2 Nivel 3: Objetivos 3 y 4, entonces la función de realización es, en general de la forma: h(n3, n4, p3, p4) = αn3 + β(n4 + p4) donde los parámetros α y β ponderarían a las correspondientes metas. El problema sería: lexmin (n1 , p2 , αn3 + β (n4 + p4 )) x∈ X s. a f i (x) + ni − pi = ui i = 1, L , p ni , pi ≥ 0 i = 1, L , p Tras realizar el nivel cero, como hemos impuesto tres niveles de prioridad tendremos que resolver a lo sumo tres problemas, correspondientes a: Nivel 1: Min n1 x∈ X s. a f 1 (x) + n1 − p1 = u1 n1 , p1 ≥ 0 R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 5 Denominamos (x1* ,n1* ,p1* ) a la solución, si n1* = 0 significa que hemos logrado verificar la meta primera y pasamos al segundo nivel. Nivel 2: Min p2 s. a x∈ X f 1 (x) + n1 − p1 = u1 n1 = 0 f 2 (x) + n2 − p2 = u2 n1 , p1 , n2 , p2 ≥ 0 La idea es, que se mantenga la meta anterior y se verifique la del nivel correspondiente, así, si volvemos a denominar (x *2 , n2* , p2* ) a la solución, si p2* = 0 significa que hemos logrado verificar la meta primera y la segunda y pasamos al tercer nivel. Nivel 3: Min α n3 + β (n4 + p4 ) s. a x∈ X f 1 (x) + n1 − p1 = u1 n1 = 0 f 2 (x) + n2 − p2 = u2 p2 = 0 f 3 (x) + n3 − p3 = u3 f 4 (x) + n4 − p4 = u4 ni , pi ≥ 0 i = 1, L,4 En este nivel como tenemos dos funciones hemos considerado como función de realización la suma ponderada de las dos y hemos impuesto que se mantengan las dos anteriores y las dos correspondientes al nivel, de forma que, si la solución obtenida, (x *3 , n3* , p3* , n4* , p4* ) , verifica que n3* = p3* = n4* = p4* = 0, x *3 será una solución satisfactoria, puesto que verifica las restricciones duras del problema, y las metas correspondientes. Con este ejemplo teórico se ha pretendido ilustrar cómo aplicar la técnica de programación por metas, no obstante, quedarían algunas consideraciones, por ejemplo, ¿cómo actuamos si en alguno de los niveles la variable no deseada no es cero?, si esto ocurre la solución correspondiente no es satisfactoria, puesto que si la variable de desviación no deseada toma un valor nos indica el incumplimiento de la correspondiente meta. En en estos casos no continuamos con el problema sino que la solución sería la que nos diera con el valor correspondiente de ni o pi, y la solución aún no siendo satisfactoria R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 6 sería la más adecuada al cumplimiento de nuestra meta, dado que minimizamos las desviaciones. A partir del incumplimiento de una meta, es decir, la no verificación del nivel, se puede actuar de varias formas. Una de ellas sería el redefinir la meta correspondiente y otra el intentar hacer una nueva distribución de funciones y niveles. De hecho, el problema no queda cerrado, sino que sería el decisor, a la vista de los resultados, el encargado de decidir qué hacer con el problema. Volviendo a nuestro ejemplo: Supongamos que la empresa establece que primero quiere maximizar los beneficios, de forma que estos alcancen un nivel de al menos 10 unidades, y que posteriormente, la contaminación se fija en un máximo de 6 unidades. Con esta información se nos genera un problema de programación por metas, en el cual los niveles corresponden a: Nivel 1: Los beneficios tienen que alcanzar un nivel de al menos 10 unidades, luego la meta es: 4x + 3y ≥ 10. Al incorporar las variables de desviación tenemos: 4x + 3y +n1 - p1 = 10. La variable no deseada es n1 y la función de realización del primer nivel es: h1(n1, p1) = n1. Nivel 2: El nivel de contaminación es como máximo de 6 unidades, luego la meta es: 3x + 2y ≤ 6. se incorporan las variables de desviación y: 3x + 2y +n2 - p2 = 6. La variable no deseada en este nivel es p2 y la función de realización del segundo nivel corresponde a: h2(n2, p2) = p2. Con esta información, el problema de programación por metas a resolver es: R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 7 lexmin (n1 , p2 ) s. a x+ y≤5 2x + y ≤ 8 x ≥1 4 x + 3y + n1 − p1 = 10 3x + 2 y + n2 − p2 = 6 x , y , ni , pi ≥ 0 i = 1, 2. Como tenemos asegurada la existencia de soluciones factibles, pasamos a la resolución por niveles. Nivel 1: Min n1 x+y≤5 s.a 2x + y ≤ 8 x≥1 4x + 3y + n1 - p1 = 10 x, y, n1, p1 ≥ 0 Aplicando el programa LINDO para programación lineal obtenemos: LP OPTIMUM FOUND AT STEP 1 OBJECTIVE FUNCTION VALUE 1) .00000000 VARIABLE N1 X Y P1 VALUE .000000 2.500000 .000000 .000000 NO. ITERATIONS= REDUCED COST 1.000000 .000000 .000000 .000000 1 Como el valor de n1 = 0 obtenemos que se ha verificado la primera de las metas y pasamos al nivel 2. R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 8 Nivel 2: Min p2 s.t x+y≤5 2x + y ≤ 8 x≥1 4x + 3y + n1 - p1 = 10 n1 = 0 3x + 2y + n2 - p2 = 6 x, y, n1, p1, n2, p2 ≥ 0 LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 1.0000000 VARIABLE P2 X Y P1 N2 VALUE 1.000000 1.000000 2.000000 .000000 .000000 NO. ITERATIONS= REDUCED COST .000000 .000000 .000000 .666667 1.000000 3 La solución obtenida es (1, 2) pero p2 = 1, lo cual nos indica que no se verifica la segunda meta, en concreto, según el resultado, el nivel se contaminación se superaría en una unidad (p2 = 1). En esta primera gráfica vamos a ver el efecto de la incorporación de la primera meta, y en la segunda gráfica, tras introducir la segunda meta observamos cómo el conjunto de soluciones satisfactorias es vacío, por tanto nuestro problema no tendría solución satisfactoria, sin embargo, la solución obtenenida, aún no siendo satisfactoria verifica la primera meta y es la más cercana al cumplimiento de la segunda, puesto que estamos minimizando la variable no deseada. R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas Gráfica nivel 1: R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz 9 Programación Matemática para Economistas 10 Gráfica nivel 2: A la vista del resultado ahora podría actuar de nuevo el decisor, puesto que él ya conoce que la imposición de 6 unidades para la contaminación no es factible. De esta forma, si mantiene la primera meta con 10 unidades y relaja la contaminación a 8, el segundo nivel se modifica y obtenemos: Nivel 2: Reformado Min p2 s.a x+y≤5 2x + y ≤ 8 x≥1 4x + 3y + n1 - p1 = 10 n1 = 0 3x + 2y + n2 - p2 = 8 x, y, n1, p1, n2, p2 ≥ 0 R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas LP OPTIMUM FOUND AT STEP 11 1 OBJECTIVE FUNCTION VALUE 1) .0000000 VARIABLE P2 X Y P1 N2 VALUE 0.000000 2.500000 0.000000 0.000000 0.500000 NO. ITERATIONS= REDUCED COST 1.000000 .000000 .000000 .000000 .000000 1 Al relajar la meta sí obtenemos una solución satisfactoria (2.5, 0), en la cual los beneficios son exactamente 10 unidades y la contaminación de 7.5 dado que n2 = 0.5. El conjunto de soluciones satisfactorias asociadas al cumplimiento de las dos metas nos lo muestra la gráfica siguiente: R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz