boletn tema 1 f_2014
Anuncio

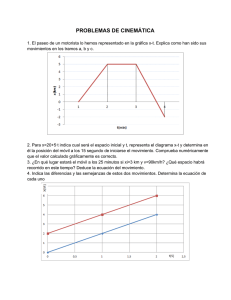
Curso 2011-2012 BOLETÍN EJERCICIOS TEMA 1 – MOVIMIENTOS 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Un automóvil circula con una velocidad media de 72 km/h. Calcula qué distancia recorre cada minuto. Un ciclista recorre una distancia de 10 km en 15 minutos. Calcula su velocidad media en metros por segundo y en kilómetros por hora. Un automóvil que circula con una velocidad constante de 90 km/h pasa por el poste indicador de 200 m en el momento en que se pone en marcha el cronómetro para medir el tiempo. ¿Cuál será su posición en el instante t = 12 s? Un automóvil que circula con una velocidad constante de 54 km/h pasa por un poste indicador en el instante t = 0. Un segundo automóvil pasa por el mismo punto en el instante t = 10 s con una velocidad de 90 km/h en la misma dirección y sentido que el primero. a) ¿Cuándo alcanzará el segundo vehículo al otro? b) ¿A qué distancia del poste indicador estarán ambos en el momento del encuentro? Dos móviles están separados inicialmente por una distancia de 300 m y comienzan a moverse simultáneamente sobre una recta dirigiéndose el uno al encuentro del otro, el primero a 36 km/h y el segundo a 72 km/h. Determina en qué posición y en qué instante se encuentran. Un automóvil que circula a 60 km/h mantiene una aceleración constante de 0’8 m/s2 durante 15 s. Calcula la velocidad que ha alcanzado al cabo de ese tiempo. Un automóvil circula con una velocidad de 72 km/h. El conductor frena y detiene el vehículo en 10 s con MRUA. Calcula el valor de la aceleración aplicada sobre el automóvil. Un camión circula a 60 km/h y acelera hasta 100 km/h manteniendo una aceleración constante de 3 m/s2. Determina el tiempo empleado y la distancia recorrida. Un móvil se mueve sobre una línea recta con una aceleración constante de 4 m/s2. Su posición inicial es 3 m y su velocidad inicial es 0’5 m/s. Halla la velocidad y la posición del móvil en el instante t = 6 s. Una piedra lanzada verticalmente desde el suelo alcanza una altura de 30 m. Calcula la velocidad inicial con que se lanzó y el tiempo que ha tardado en llegar a esa altura. ¿Cuál es la velocidad angular en el SI de un motor que gira a 2000 rpm? Una motocicleta da vueltas a una pista circular de 50 m de diámetro con una velocidad constante de 54 km/h. Calcula: a) El espacio que recorre sobre la circunferencia cada 10 s. b) La velocidad angular. c) El espacio angular. Para hallar la altura de una torre se deja caer un objeto desde su punto más alto y se mide que tarda 6 s en llegar al suelo. ¿Cuál es la altura de la torre? C O L E G I O M A R Í A A U X I L I A D O R A. S A L E S I A N A S. C Á D I Z Avda. Andalucía, 70.11008 CÁDIZ. www.cadiz.salesianas.com Tel: 956 25 16 07 Fax: 956 26 06 64 Curso 2011-2012 14. Calcula la velocidad del SI. 15. Desde lo alto de un tiempo que desde el m/s. Halla la altura cruzarse. angular de cada una de las agujas de un reloj en unidades edificio de 50 m de altura se deja caer un objeto al mismo suelo se lanza verticalmente otro objeto con velocidad de 40 a la que se cruzan los dos objetos y el tiempo que tardan en C O L E G I O M A R Í A A U X I L I A D O R A. S A L E S I A N A S. C Á D I Z Avda. Andalucía, 70.11008 CÁDIZ. www.cadiz.salesianas.com Tel: 956 25 16 07 Fax: 956 26 06 64 Curso 2011-2012 1. Un coche que lleva una velocidad inicial de 2 m/s, acelera durante 10 segundos con aceleración constante de 3 m/s2. ¿Qué velocidad tendrá a los 10 segundos? (32 m/s) ¿Qué posición tendrá en dicho instante, si en el instante inicial está en la posición - 3 m? (167 m) ¿Qué espacio habrá recorrido en dicho tiempo? (170 m) 2. Dos trenes A y B viajan uno hacia el otro por dos vías paralelas encontrándose a 3’5 km. de distancia cuando empezamos a contar el tiempo. El tren A lleva una velocidad de 108 km/h y el B, 144 km /h. a) Calcula en qué momento pasará un tren junto al otro. (50 s) b) Calcula la distancia que existirá entre las máquinas de ambos trenes dos minutos después de empezar a contar el tiempo. 3. En una carrera ciclista que se desarrolla por una carretera recta, a las 12 de la mañana, un ciclista A, aventaja a otro B, en 6 km. Si el que va primero, lleva una velocidad constante de 36 km/h y el que va segundo, va una velocidad constante de 54 km/h, ¿le habrá alcanzado a las 12 y cuarto? (No) Si no le ha alcanzado, ¿en qué momento y en qué instante le alcanzará? (1200 s y 12000 m) 4. Dos trenes A y B viajan en el mismo sentido por dos vías paralelas encontrándose el tren A, 2 km. por delante del B cuando empezamos a contar el tiempo. El tren A lleva una velocidad de 108 km/h y el B, 144 km /h. a) Calcula en qué momento alcanzará el tren B al A. (200 s) b) Calcula la distancia que existirá entre las máquinas de ambos trenes 5 minutos después de empezar a contar el tiempo. 5. Hallar la velocidad de un móvil que se mueve en línea recta y que se encuentra en la posición -5 m en el instante 2 segundos y en la posición 10 metros en el instante 5 segundos. (5 m/s) ¿Qué posición tendrá en el instante inicial y en el instante 20 segundos? (e0=-15 m; e20=85 m) 6. Un conductor cometiendo una grave infracción de tráfico, va por una carretera a 144 km/h, en un instante dado, ve un obstáculo a 75 m de distancia y frena con aceleración de 8 m/s2. a) ¿Se detendrá antes de chocar? (No) b) Si hubiera ido a 90 km/h, ¿qué hubiera pasado? (no chocaría) 7. Desde la ventana de un 4º piso se cae una maceta al suelo y tarda 2 segundos. ¿A qué altura está dicho piso y con qué velocidad llega al suelo la maceta? (19’6 m; -19’6 m/s) 8. Se lanza un cuerpo verticalmente hacia arriba con una velocidad de 30 m/s. Calcular: a) La altura máxima alcanzada y el tiempo que tarda en alcanzarla. (3’06 s; 46’41 m) b) ¿Qué velocidad tendrá y cuánto tiempo le costará llegar a 3/4 de la altura máxima alcanzada? (1’55 s; 14’75 m/s) 9. La velocidad de un tren se reduce uniformemente de 108 km/h a 72 km/h. Sabiendo que durante ese tiempo recorre una distancia de 100 m. Calcular: a) La aceleración de frenado. (-2’5 m/s2) b) La distancia que recorre, si sigue con esa misma aceleración, hasta que se para y el tiempo que tarda en hacerlo. (8 s; 80 m) C O L E G I O M A R Í A A U X I L I A D O R A. S A L E S I A N A S. C Á D I Z Avda. Andalucía, 70.11008 CÁDIZ. www.cadiz.salesianas.com Tel: 956 25 16 07 Fax: 956 26 06 64 Curso 2011-2012 10. El autobús que une Zaragoza con Huesca pasó por el km 26 a las 10 horas y por el km 46 a las 10:15 horas. a) ¿Cuál ha sido la velocidad media en dicho tramos? Exprésala en km/h y en m/s. (80 km/h; 22’2222 m/s) b) Si la distancia entre la dos ciudades es de 72 km, y en todo el trayecto consigue esa velocidad media, ¿qué tiempo le costará? (3240 s) 11. Un ciclista que circula con una velocidad constante de 36 km/h, pasa por un punto a las 10 horas. 15 minutos más tarde pasa por el mismo punto, un coche con una velocidad constante de 108 km/h en la misma dirección y sentido. a) ¿Cuándo tardará el coche en alcanzar al ciclista? (450 s) b) ¿A qué distancia del punto estarán ambos en el momento que lo alcanza? (13500 m) 12. Una noria de 5 m de radio gira con una velocidad de 2,5 m/s. Calcula. a) La velocidad angular y el periodo. (0’5 rad/s; 12’6 s) b) El número de vueltas que dá en 5 minutos. 13. ¿Cuál es la velocidad angular de un motor que gira a 3 000 r.p.m.? (314 rad/s) 14. Calcula la velocidad angular de las ruedas de un coche que va a 108 km/h, sabiendo que tienen un diámetro de 75 cm. (80 rad/s) 15. Una noria tarda 30 segundos en dar una vuelta completa. Si tiene velocidad angular constante, calcula: a) La frecuencia. (0’033 Hz) b) La velocidad angular de la noria. (0’21 rad/s) c) La diferencia de velocidad lineal de dos personas subidas en la noria, una situada a 15 m y otra a 10 m del eje de giro. (3’15 – 2’1=1’05 m/s) 16. El motor de un coche gira a 2 400 r.p.m. Hallar: a) La velocidad angular. (251’2 rad/s) b) El número de vueltas que dará en 20 segundos. (800 vueltas) c) El tiempo que le cuesta girar un ángulo de 120 radianes. (3 s) 17. Un ciclista da vueltas en una pista circular de 70 m de diámetro a una velocidad de 60 km/h. Calcula: a) La velocidad angular y el tiempo que tarda en dar una vuelta. (0’476 rad/s; 13’2 s) b) La frecuencia y la distancia recorrida en 30 minutos. (0’0758 Hz; 30000 m) 18. Las ruedas de un coche tienen 80 cm de diámetro. ¿Qué espacio recorre en media hora el coche cuando las ruedas giran con una velocidad angular de 75 rad/s? (54000 m) 19. Un coche circula a 120 km/h por una pista circular. Si tarda 3,79 s en dar media vuelta, calcula: a) La velocidad angular y el radio de la pista. (0’829 rad/s; 40’21 m) C O L E G I O M A R Í A A U X I L I A D O R A. S A L E S I A N A S. C Á D I Z Avda. Andalucía, 70.11008 CÁDIZ. www.cadiz.salesianas.com Tel: 956 25 16 07 Fax: 956 26 06 64