INTRODUCCIÓN AL ANÁLISIS DE COSTOS
Anuncio

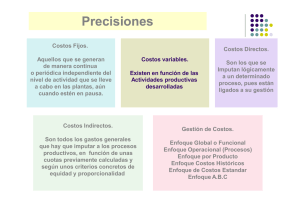
INTRODUCCIÓN AL DESARROLLO DE PROYECTOS Y PROTOTIPOS Miguel Hesiquio Garduño. DIQP-ESIQIE INTRODUCCIÓN AL ANÁLISIS DE COSTOS. De una manera aproximada, podemos clasificar a los costos en 2 grandes categorías ♦Costos Fijos Costos Totales ♦Costos Variables Costos Fijos: Los costos fijos son independientes del volumen o nivel de producción PARA UN INTERVALO ESPECÍFICO.. Es decir, que no importa si producimos 1000 piezas o ninguna, estos no varían.Sin embargo, si queremos producir 20000, hay que revisar la capacidad instalada. ( recordemos la historia de “Canastitas en Serie” de B. Traven) Ejemplos: Renta, Salario de Ejecutivos, Personal Operativo, Gasto de inversión inicial. Costos Variables: Son dependientes del volumen o nivel de producción a mayor cantidad de producto, el costo variable total. Ejemplos: materias primas, energía eléctrica, combustible. En ocasiones se cuenta la mano de obra directa (obreros), cuando por necesidad de aumentar la producción o atender a más público se contrata personal por temporada. (Esto lo podemos ver en las tiendas departamentales cuando es temporada verano o invierno contratan personal para 3 meses) Costo total CT Es una manera simple, podemos decir que el costo total es la suma de los costos fijos totales C FT y los costos variables totales (CVT) es decir: CT= CFT+ CVT El Costo Total se puede describir también como una función de las unidades producidas “P”, conocido el costo variable por unidad CVU. La expresión que define al costo total es: CT (P)=CFT+ CVU*P Que es la forma más simple, pues corresponde a la ecuación de una recta. Otras funciones importantes son Costo Medio total CM, C Nos referimos al costo promedio de producir una unidad, tomando en cuenta que CT es función de P. CM= C= CT (P)/P Costo Marginal: Es la adición al costo total, atribuido a la producción de una unidad más, CMG= C’ (P) Venta Total: INTRODUCCIÓN AL DESARROLLO DE PROYECTOS Y PROTOTIPOS Miguel Hesiquio Garduño. DIQP-ESIQIE Es el importe obtenido con la venta de P piezas, el modelo más sencillo es una línea recta. (Lineal), al precio Vu (precio unitario) VT=Vu*P Utilidad Total (UT): Es la ganancia, resulta de restar, a la venta total, el costo total UF= VT- CT Si presentamos la grafica de las funciones de costo total CT y la venta total. (Suponiendo casos ideales) Observamos que las ecuaciones se introducen, este punto denomina punto de equilibrio P.E., que es el punto en el cual no se tiene ganancias, pero tampoco perdidas, es decir, que importe de la venta total es igual al de los costos totales. VT= CT Por debajo de este valor (P.E.) se tienen perdidas UT<0, el costo total es mayor que la venta total. Por arriba del P.E. se comienza a tener ganancias UT>0. Otro grafico que podemos elaborar es el de la utilidad total en función del numero de artículos P. que nos muestra precisamente lo comentado en el párrafo anterior. Cuando la función de CT no es lineal, es posible que existan 2 P.E. Y además un máximo en la utilidad y obviamente un mínimo en los costos totales. Un Ejemplo de funciones sencillas: Un fabricante de grabadoras tiene un costo fijo mensual de 10,000 un costo de producción de $15 por unidad y un precio de venta por unidad de $15, calcular: a) CT c) VT d) VT e) El punto de equilibrio (P.E.) Ejemplo 2. Un fabricante de muñecas tiene 2 siguientes costos totales, en función de las unidades producidas, el precio de venta por unidad es de $ 20 Cantidad P Costo total CT (Pesos) 1 2 3 4 5 6 7 8 9 10 11 110 116 121 126 130 136 143.5 156 172 190 209 a) Hallar la relación funcional para el Costo Total b) Hallar la ecuación de Costo Medio. c) Hallar la función de Venta Total d) Hallar el Punto de Equilibrio e) Hallar la función de Utilidad Total. f) Hacer los incisos c) al d) tomando un precio de Venta por unidad de: $ 15 y $ 25. Nota: aproximar la relación funcional a una recta (CT) y ensayar a una parábola.