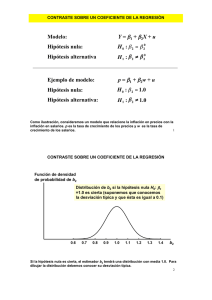
En un estudio para aumentar la supervivencia (variable y en tanto
Anuncio

Métodos de Regresión (Grado en Estadística y Empresa) Ejercicio de resumen En un estudio para aumentar la supervivencia (variable y en tanto por ciento) de determinada clase de plantas se utilizan concentraciones de tres productos (variables x1, x2 y x3 en gramos). Para distintos valores de las variables x1, x2 y x3 se obtienen los siguientes porcentajes de aumento de la supervivencia: y 25.5 31.2 25.9 38.4 18.4 26.7 26.4 25.9 32 25.2 39.7 35.7 26.5 x1 1.74 6.32 6.22 10.52 1.19 1.22 4.10 6.32 4.08 4.15 10.15 1.72 1.70 x2 5.30 5.42 8.41 4.63 11.60 5.85 6.62 8.72 4.42 7.60 4.83 3.12 5.30 x3 10.80 9.40 7.20 8.50 9.40 9.90 8.00 9.10 8.70 9.20 9.40 7.60 8.20 a) Ajustar los datos a un modelo de regresión lineal múltiple que explique el porcentaje de aumento de la supervivencia en función de las concentraciones de los tres productos que inciden sobre la supervivencia de las plantas. b) Realizar la estimación de la varianza. c) Construir un intervalo de confianza al 95% para la respuesta media cuando x1=3, x2=8 y x3=9. d) Construir un intervalo de predicción al 95% para una respuesta individual del porcentaje de supervivencia cuando x1=3, x2=8 y x3=9. e) Realizar el contraste de hipótesis β2=-2.5 contra β2>-2.5 para un nivel de significación del 5%. f) Calcular el coeficiente de determinación R2 y realizar también el contraste de significación conjunta de la regresión. g) Realizar el contraste de significación individual parámetro a parámetro. h) Escribir la tabla ANOVA. i) Si los valores propios de la matriz de correlaciones entre las variables explicativas son 0.8227, 0.9253, 1.2520, determina si es posible que existan problemas de multicolinealidad. j) Determina si existen puntos palanca (leverage points). k) Determina si la observación nº 5, (18.4, 1.19, 11.60, 9.40), es influyente o no, según la distancia de Cook. Para realizar el ejercicio puedes ayudarte de las siguientes matrices y cálculos: ⎛ 8.0648 − 0.0826 − 0.0942 − 0.7905 ⎞ ⎜ ⎟ 0.0017 0.0037 ⎟ ⎜ − 0.0826 0.0085 −1 ( X' X) = ⎜ − 0.0942 0.0017 0.0166 − 0.0021⎟ ⎜ ⎟ ⎜ − 0.7905 0.0037 − 0.0021 0.0886 ⎟ ⎝ ⎠ ⎛ 377.5 ⎞ ⎜ ⎟ ⎜1877.567 ⎟ X' Y = ⎜ 2246.661⎟ ⎜ ⎟ ⎜ 3337.78 ⎟ ⎝ ⎠ diag( H ) = ( 0.4660, 0.1432, 0.4296, 0.3823, 0.5801, 0.2497 , 0.1524, 0.2204, 0.1426, 0.1114, 0.3975, 0.4993, 0.2254 ) ' Y' Y = 11400.15 1' Y = 377.5