Aplicaciones de las leyes de Newton Fuerza de fricción
Anuncio
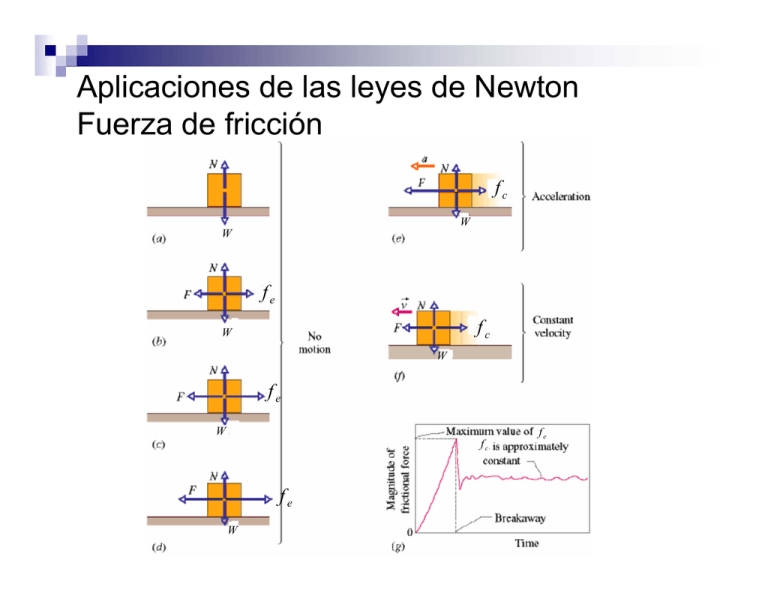
Aplicaciones de las leyes de Newton Fuerza de fricción fc W W fe fc W W fe W fc fe W fe Propiedades de la fuerza de fricción 1. Si el cuerpo no se mueve, la fuerza de fricción estática fe y la fuerza aplicada F se cancelan (tienen igual magnitud, pero son opuestas en dirección). 2. La magnitud de fe tiene un valor máximo fe,max = µe N, donde µe es el coeficiente de fricción estático y N es la fuerza normal. Si la fuerza aplicada F excede este valor fe,max entonces el cuerpo comienza a deslizarse en la superficie. 3. Una vez el cuerpo empieza a moverse, la magnitud de la fuerza de fricción se reduce a un valor fc dado por fc,max = µc N, donde µc es el coeficiente de fricción cinético. Nota: µc < µe Ejemplo: Dos niños son arrastrados en un trineo sobre un terreno cubierto de nieve. El trineo es tirado por una cuerda que hace un ángulo de 40° con la horizontal. La masa conjunta de los niños es de 45 kg y la del trineo es 5 kg. Los coeficientes de fricción son µe = 0.2 y µc = 0.15. Determinar la aceleración de los niños y el trineo si la tensión es (a) 100 N y (b) 140 N. G N G G W = mg Ejemplo: La masa m2 de la figura se ha ajustado de manera tal que el bloque de masa m1 está a punto de deslizarse. Si m1 = 7 kg y m2 = 5 kg, calcula el coeficiente de fricción estático entre el bloque y la superficie. Con un ligero golpe, los bloques se deslizan con aceleración a. Si µc = 0.54, calcula el valor de a. Velocidad Terminal 1 2 D = C ρ Av 2 W − D = ma Después de cierto tiempo, D = W y el objeto baja con rapidez constante vt. 1 2 mg − C ρ Avt = 0 2 2mg vt = Cρ A Movimiento circular uniforme 2 v ac = r Fuerza Centrípeta Un astronauta es entrenado en una centrífuga horizontal de radio igual a 5 m. Calcula la aceleración centrípeta cuando la velocidad lineal de la centrífuga es de 15 m/s. 2~3 g piloto se siente bien pesado, 4g visión cambia a blanco y negro. Puede perder conocimiento si aceleración se sostiene varios minutos Ejemplo: En una prueba de deslizamiento, un carro recorre una pista circular de radio igual a 45.7 m en 15.2 s sin patinar y con rapidez constante. Calcula (a) la rapidez, (b) la aceleración centrípeta y (c) el valor mínimo del coeficiente de fricción estático. Ejemplo: Una curva de radio 30 m tiene un ángulo de inclinación θ. Determinar el valor de θ para el cual un carro puede tomar la curva a 40 km/hr (11.1 m/s) aunque la carretera no posea rozamiento. θ Ejemplo: Se hace girar un cubo de agua siguiendo una circunferencia vertical de radio r. Si la velocidad en la parte más alta es vt, calcular (a) la fuerza ejercida por el cubo sobre el agua, (b) el valor mínimo de vt para que el agua no salga del cubo y (c) la fuerza ejercida por el cubo en la parte más baja en donde la velocidad es vb.