Sistema bien condicionado
Anuncio

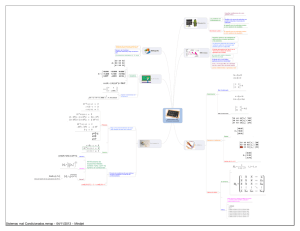
Práctica 5 Aplicaciones de los sistemas lineales (II) Aplicaciones de los sistemas lineales (II) La ecuación del calor en una placa Condicionamiento de una matriz Interpolación polinómica. Matriz de van der Monde Integración numérica. Matriz de Hilbert Ecuación del Calor en un rectángulo N W C E S –1 –1 TC = (TW + TN + TS + TE)/4 4 –1 Molécula –1 Sistema de ecuaciones lineales tomando 9 nodos 50 0 0 50 50 T1 T4 T7 T2 T5 T8 T3 T6 100 100 T9 0 100 50 −1 4 −1 −1 4 −1 −1 4 4 −1 −1 −1 −1 −1 −1 −1 4 −1 −1 50 50 T1 50 T 0 2 T3 50 −1 T 50 −1 4 T5 = 0 −1 −1 4 −1 T6 50 T 150 4 −1 7 −1 4 −1 T8 100 −1 −1 4 T9 150 Algoritmo para generar la matriz (calor2D) Entrada: n,m dimensiones de la matriz. Salida: A matriz del sistema. Proceso: % cálculo de las diagonales 1 y –1. p = n*m; v = ones(1,p-1); for k = n:n:p-n, v(k) = 0; end % cálculo de las diagonales n y –n. w = ones(1,p-n); % Matriz del sistema A = 4*eye(p)- diag(v,1) - diag(v,-1)- diag(w,n) - diag(w,-n); Limitaciones de los Métodos Directos Acumulación del error de redondeo Coste de la eliminación: O(n3) Sensibilidad al error de redondeo Sistemas mal o bien condicionados Número de condición Estrategia de Pivotación Parcial Llenado de la matriz Sensibilidad al error de redondeo Sistema mal condicionado : Un pequeño cambio en la matriz causa un gran cambio en la solución. Sistema bien condicionado : Pequeños cambios en la matriz causan pequeños cambios en la solución. Condicionamiento de una matriz Número de condición de una matriz cond mide el mal condicionamiento cond(eye(n))=1 cond(matsingular) = inf rcond mide el buen condicionamiento rcond(eye(n))=1 rcond(matsingular) = 0 rcond y det Pivotación parcial Un algoritmo deficiente puede arruinar un sistema bien condicionado. Estrategia: Elegir como pivote el elemento de mayor valor absoluto del resto de la columna. El operador \ para resolver Ax = b Interpolación polinómica Matriz de van der Monde Determinar un polinomio Pn(x) = an+1 + anx + an-1x2 + ... + a1xn de grado no superior a n, que pase por n+1 puntos dados (x1, y1), (x2, y2),..., (xn+1, yn+1), Al imponer las condiciones queda un sistema lineal con matriz asociada al matriz de van der Monde. 1 x1 x12 2 1 x x 2 2 1 x3 x32 M M M 2 1 x x n+1 n+1 L x1n an+1 y1 n L x2 an y2 L x3n ⋅ an−1 = y3 M M M L xnn+1 a1 yn+1 Integración numérica Matriz de Hilbert Determinar los coeficientes del polinomio p(x) de modo que cumplan ∫ 1 0 xk p( x ) dx = ∫ 1 0 xk f ( x ) dx, k = 0, 1, 2, 3 siendo f(x) una función dada. Imponiendo las condiciones obtenemos otro sistema lineal cuya matriz asociada es la denominada matriz de Hilbert . 1 1 / 2 1 / 3 1 / 4 1/ 2 1/ 3 1/ 4 1/ 3 1/ 4 1/ 5 1/ 4 1/ 5 1/ 6 1 / 5 1 / 6 1 / 7