conceptos básicos sobre la heterocedasticidad en el modelo básico

Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
CONCEPTOS BÁSICOS SOBRE LA
HETEROCEDASTICIDAD EN EL
MODELO BÁSICO DE REGRESIÓN
LINEAL
TRATAMIENTO CON E-VIEWS
Rafael de Arce y Ramón Mahía
Dpto. de Economía Aplicada
Universidad Autónoma de Madrid
rafael.dearce@uam.es
ramon.mahia@uam.es
(Revisado marzo2008)
1
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
2
ÍNDICE DE CONTENIDOS
CONCEPTOS BÁSICOS SOBRE LA HETEROCEDASTICIDAD EN EL MODELO
BÁSICO DE REGRESIÓN LINEAL ........................................................................................ 1
1.- Qué es .................................................................................................................... 3
2.- Causas frecuentes de heterocedasticidad ............................................................ 3
3.- Efectos de la heterocedasticidad sobre el MBRL ............................................... 5
4.- Cómo se detecta la presencia de Heterocedasticidad ......................................... 7
A. Contrastes Gráficos ............................................................................................... 7
A.1) Gráfica del error a través de las distintas observaciones del modelo ............... 7
A.2) Gráfica del valor cuadrático del error y los valores de “Y” y “X’s” ................ 8
B. Contrastes numéricos ............................................................................................ 8
B.1.) Contraste de Glesjer......................................................................................... 8
B.2.) Contraste de Breusch-Pagan ............................................................................ 9
B.3.) Contraste de White (prueba general de heterocedasticidad de White) .......... 10
B.4.) Contraste a partir del coeficiente de correlación por rangos de Spearman ... 12
5.- Cómo se corrige ................................................................................................... 13
TRATAMIENTO DE LA HETEROCEDASTICIDAD EN E-VIEWS ............................... 15
EJEMPLO PRÁCTICO DE ANÁLISIS DE HETEROCEDASTICIDAD ......................... 22
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
3
1.- Qué es1
El modelo básico de regresión lineal exige que la varianza condicional de las perturbaciones
aleatorias a los valores de los regresores X sea constante:
Var (u i / X i ) = σ 2
aunque generalmente la hipótesis se formula sin mencionar el carácter condicional de la
varianza, simplemente como:
Var (u i ) = σ 2
Para comprender de forma intuitiva esta restricción podemos razonar del siguiente modo.
Iguales varianzas de “u” para los distintos valores de “x” implica necesariamente igual
dispersión (varianzas) de “y” para distintos valores de “x” lo que implica necesariamente que la
recta de regresión va a representar con igual precisión la relación entre “x” e “y”
independientemente de los valores de “x”. Esto es muy importante porque debe recordarse
que el análisis de regresión es un análisis de regresión condicional de “y” sobre “x” lo cual
implica, por lógica, que si se desea obtener un parámetro de relación estable y útil entre ambas
variables, los valores muestrales de “y” deben mostrarse igualmente dispersos ante variaciones
de “x”. Dicho de otro modo, y en términos del error, aunque el error será mayor para mayores
valores de “x” (no se fuerza que el error tenga un tamaño igual para el recorrido de “x”) la
dispersión del error alrededor de la recta de regresión será la misma. Esto permite considerar
igualmente válidos todos los datos muestrales de los regresores “x” para determinar la relación
condicional de “y” a los valores de “x” sin tener que ponderar más o menos unos valores u otros
de “x” en función de la menor o mayor dispersión de “y” en los distintos casos.
En un plano puramente analítico, la matriz de varianzas-covarianzas de las perturbaciones de un
modelo heterocedástico se representaría del siguiente modo:
 E (u1 ) 2
.   E (u1 ) 2

 
E (u1u 2 ) E (u 2 ) 2

= 0
E (UU ' ) =

  0
...

 
2
E (u n )   0
 E (u1u n ) E (u 2 u n )


 = σ 2 I = σ 2Σ
i n

...

0 E (u n ) 2 
.
E (u 2 )
0
0
2
Como ya se vio en el capítulo introductorio sobre el estimador de Aitken, en el caso concreto de
la presencia de una matriz de varianzas-covarianzas no escalar de las perturbaciones aleatorias,
la estimación máximo verosímil de los parámetros del modelo resulta ahora:
β MCG = [X ' Σ −1 X ] X ' Σ −1Y
−1
Un estimador que goza de buenas propiedades estadísticas (lineal, insesgado, eficiente y
consistente ).
2.- Causas frecuentes de heterocedasticidad
Aunque las que se citan a continuación no son las únicas posibilidades que dan lugar a un
modelo heterocedástico, sí son las más frecuentes.
1
Etimológicamente, por cierto, la palabra deriva de “hetero” (distinto) y el verbo griego “skedanime” que
significa dispersar o esparcir.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
4
A.- Causas relacionadas con la selección de variables exógenas:
A.1- Variables explicativas con una distribución asimétrica
Si una variable explicativa presenta una distribución asimétrica (por ejemplo la renta), resultará
inevitable que, por ejemplo para el caso de asimetría a derechas, los valores mayores del
regresor estén asociados a una mayor dispersión en el término de error de la regresión.
A.2- Variables explicativas con amplio recorrido
Las variables con amplio recorrido favorecen la aparición de heterocedasticidad en mayor
medida que aquellas otras que presentan un agrupamiento muy claro alrededor del valor de la
media. Esto no es tan evidente como el efecto de la asimetría pero, en cierto modo, y dado que
trabajamos con muestras, la selección de una muestra que favorezca la heterocedasticidad es
más probable en el caso de variables con amplios recorridos que con escasas varianzas. Este
riesgo es especialmente elevado en los modelos de corte transversal ya que la selección de los
elementos muestrales es arbitraria (no viene determinada por el paso del tiempo y, por tanto,
puede incurrir en el riesgo de mezclar muestras provenientes de poblaciones diferentes) por lo
que la muestra pueden agrupar, casualmente, grupos de observaciones que presenten valores
muy dispersos y poco dispersos al mismo tiempo.
A.3.- Omisión de variables relevantes en el modelo especificado.
En este caso no hablamos de las variables seleccionadas, sino, precisamente, de las no
seleccionadas. Cuando se ha omitido una variable en la especificación, dicha variable quedará
parcialmente recogida en el comportamiento de las perturbaciones aleatorias, pudiendo
introducir en éstas su propia variación, no necesariamente fija.
Recuérdese que la hipótesis inicial del MBRL de homocedasticidad hacía referencia a la
varianza constante de las perturbaciones aleatorias, pero no obligaba a que las variables
explicativas tuvieran también varianza constante, hecho que, además, sería una restricción muy
poco plausible.
B.- Otras causas
B.1.- Cambio de estructura
El hecho de que se produzca un cambio de estructura determina un mal ajuste de los parámetros
al conjunto de los datos muestrales. Este no tiene porque influir del mismo modo en todo el
recorrido de la muestra2, pudiendo producir cuantías de desajuste del modelo diferentes y, por
tanto, varianza no constante por subperíodos.
B.2. Forma funcional incorrecta
La utilización de una forma funcional incorrecta, por ejemplo la utilización de una función
lineal en lugar de una logarítmica potencial, puede provocar que la calidad del ajuste de la
regresión varíe según los valores de las exógenas, por ejemplo, ajustando bien para los valores
pequeños y mal para los grandes; en ese caso, es posible que en las zonas de peor ajuste existan,
no sólo errores mayores, sino también errores más dispersos.
2
De hecho, los parámetros estimados "recogerán mejor" el comportamiento de la serie en aquella de las dos
estructuras distintas que se produzca durante mayor número de observaciones, ya que los parámetros estimados en
presencia de un cambio de estructura serán una media ponderada de los que resultarían de una estimación particular
para cada una de las dos submuestras
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
5
B.3.- Modelos de aprendizaje sobre los errores
Esta causa, apuntada por Gujarati3, se refiere a la modelización de fenómenos que contienen un
mecanismo de auto - aprendizaje en función de los errores (desajustes) previos. En este tipo de
fenómenos, el paso del tiempo implica progresivamente, no sólo un menor tamaño del error,
sino además una varianza progresivamente inferior.
B.4.- Presencia de puntos atípicos
La presencia de algunos valores atípicos en la muestra de datos implicará necesariamente un
desajuste en la varianza de la perturbación (en cierto modo, un punto atípico puede considerarse
un elemento muestral perteneciente a otra distribución y, por tanto, potencialmente con varianza
distinta).
En todo caso, sea cuál sea el origen del problema, en muchas ocasiones es posible asociar la
varianza no constante de las perturbaciones aleatorias a los valores de alguna de las variables
incluidas4 en el modelo. Dicho de otro modo, podría suponerse que la varianza de la
perturbación se compone de una parte constante, homocedástica, y otra que varía según los
valores de una determinada variable Zi:
σ i2 = f (σ 2 Z i )
donde σ 2 sería la parte fija de la varianza, y Zi la variable o incluso la matriz de variables cuyos
valores se asocian con los cambios en la varianza de las perturbaciones aleatorias.
Es muy probable que esta asociación entre el proceso de heterocedasticidad y una determinada
variable o una combinación de ellas sea algo simplista, probablemente no sea muy realista y y
quizá no alcance a ser completamente satisfactoria para explicar el patrón de “movimiento” de
la varianza. Sin embargo, asumir este tipo de conexión entre varianza de “U” y una/s variable/ss
está en la base de la mayoría de los procedimientos de detección de la heterocedasticidad y,
desde luego, resulta imprescindible para los mecanismos de solución de la heterocedasticidad.
Efectivamente, este tipo de función podría ser empleada precisamente como el “supuesto
simplificador” al que anteriormente se hacía referencia para posibilitar la estimación mediante
MCG sin encontrarnos con más incógnitas (elementos de la matriz Σ) que observaciones.
3.- Efectos de la heterocedasticidad sobre el MBRL
En términos generales, los efectos de la presencia de heterocedasticidad sobre el MBRL
estimado con Mínimos Cuadrados Ordinarios son:
-
3
El estimador de Mínimos Cuadrados Ordinarios sigue siendo lineal, insesgado y
consistente pero deja de ser eficiente (varianza mínima). Es interesante recordar que la
homocedasticidad de la perturbación no juega ningún papel relevante en la insesgadez o
la consistencia, propiedades muy importantes que si se alteran, sin embargo, ante la
presencia de regresores estocásticos o, en muchas ocasiones, ante la omisión de
variables relevantes.
Econometría. D.N Gujarati. Ed. Mc Graw Hill.
En realidad, cabe también pensar en la posibilidad que el patrón de heterocedasticidad esté relacionado con los
valores de alguna variable no incluida en el modelo (una variable omitida, consciente o inconscientemente) aunque,
en general, y quizá por un criterio de sencillez operativa, los métodos de corrección y detección se suelen concentrar
en la lista de variables exógenas incluidas en la especificación.
4
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
-
6
Las varianzas del estimador de Mínimos Cuadrados Ordinarios, además de no ser
mínimas, no pueden calcularse con la expresión utilizada en presencia de
homocedasticidad ( V ( β ) = σ 2 ( X ' X ) ) o, dicho de otro modo, esta expresión es un
estimador sesgado de la verdadera varianza de los parámetros; alternativamente, debe
−1
−1
utilizarse la expresión cov − var( βˆ ) = σ 2 [ X ' X ] X ' ΣX [ X ' X ] de modo que, si se
sigue utilizando la expresión de MCO, se cometerá un error de cálculo lo que implica,
básicamente, que nuestros cálculos “t” ya no se distribuirán como una “t”, el contraste
“F” ya no se distribuirá como una “F” o los contrastes LM ya no seguirán una ChiCuadrado.
−1
Ante estos dos problemas, caben en realidad distintos escenarios en función de la estrategia
elegida por el modelizador:
1.- Utilizar MCO considerando la presencia de heterocedasticidad
En ese caso, aún resolviendo el problema de cálculo, seguimos enfrentando un problema de
eficiencia lo cual significa, en todo caso, que los contrastes de significación habituales “t”, “F”,
Chi-Cuadrado tenderían a ser más exigentes, a ofrecer resultados menos concluyentes al tiempo
que los intervalos de confianza habitualmente computados para los parámetros tenderán a ser
más amplios.
2.- Utilizar MCO ignorando la heterocedasticidad
En este caso, tenemos una varianza que, dado el error de cálculo es un estimador sesgado del
verdadero valor de la varianza (valor correctamente calculado) sin que, en general, se pueda
saber si ese cálculo incorrecto sobreestima o subestima el verdadero valor. Así pues, las
conclusiones derivadas de la utilización de los contrates habituales son, sencillamente,
incorrectas.5 Conviene además tener en cuenta que el problema del cálculo incorrecto deriva en
realidad de que el estimador insesgado de la varianza de la perturbación ya no resulta ser:
σ~ 2 =
e' e
n−k
de modo que, además del error de cálculo en la estimación de la varianza de los parámetros,
todos aquellos contrastes o tests basados en este estimador insesgado serán también incorrectos.
En todo caso, un error frecuente consiste en pensar que cualquier cálculo que implique la
utilización de los errores de un modelo heterocedástico será incorrecto cuando, en realidad, no
es así. Un ejemplo interesante es el cálculo del coeficiente de determinación R2 (o su versión
corregida) que no se ve afectado por la existencia de heterocedasticidad. La razón estriba en que
el cálculo de la R2 se realiza a partir del cálculo de las varianzas poblaciones de “u” (σu) y de
“y” (σy) y el hecho de que utilicemos conceptos poblaciones, no muestrales, implica que
5
Sobre esta reflexión puede ser interesante recordar un par de experimentos. El primero, realizado por Goldfeldt y
Quandt en 1972 (Non Linnear Methods in Econometrics. North Holland, pp 280.) llegó a dos conclusiones: (1) que la
pérdida de eficiencia de MCO respecto a MCG puede ser de hasta 10 veces en el parámetro constante y de 4 veces en
los parámetros que acompañan a variables explicativas y (2) que el cálculo incorrecto de de la varianza de los
estimadores ignorando la heterocedasticidad produce en general un sesgo por infravaloración de la real del orden del
doble. El segundo, realizado por Davidson y Mackinnon en 1993 (Estimation and Inference in Econometrics, OUP,
Nueva Cork, 19993, pp. 549-550) concluyó que el uso de MCO (con o sin corrección) sobreestima consistentemente
el verdadero error estándar de los parámetros obtenido mediante el procedimiento correcto (MCG) mientras que la
utilización de MCO sin corregir tienden a ofrecer menores varianzas que las obtenidos por MCO corregidos, para los
parámetros de pendiente, y mayores para el término independiente.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
7
utilizamos varianzas no condicionales a los valores de “x” de modo que la R2 (poblacional) no
se ve afectada por la presencia de heterocedasticidad; de hecho, la expresión σ~ 2 = e' e n
estima consistentemente la varianza del error poblacional (σu).
3.- Utilizar MCG
Es evidente que esta parece la mejor de las soluciones aunque también debe observarse que
utilización de este estimador exigiría conocer o estimar de antemano los valores de los
elementos de Σ. Estimar las “n” varianzas distintas de Σ partiendo de “n” observaciones y “k”
variables explicativas es imposible, de modo que, como se verá más adelante, la utilización de
este estimador exigirá asumir algún supuesto simplificador sobre la causa de una eventual
heterocedasticidad, un supuesto simplificador que permita a su vez determinar, de forma
también simplificada, la forma de la matriz Σ. Evidentemente, encontrar una simplificación
correcta de Σ dotará de plena utilidad (eficiencia) a la estimación con MCG pero, a sensu
contrario, un mal diseño de la causa de la heterocedasticidad y su expresión en Σ no garantizará
esa eficiencia.
4.- Cómo se detecta la presencia de Heterocedasticidad
Antes de entrar a enumerar y revisar brevemente los principales procedimientos deben quedar
claras dos cuestiones preliminares:
1.- Resultará imposible observar directamente la presencia de heterocedasticidad ya que, en la
mayoría de los análisis econométricos, sólo dispondremos de un valor de “Y” para cada valor de
“X” (y por tanto de un único valor de “U”) por lo que resulta conceptualmente imposible
observar si la varianza de las “U” para cada valor de “X” es la misma. Por tanto, la mayor parte
de los métodos se apoyarán en los residuos obtenidos en un modelo previo (estimado
generalmente con MCO); estos residuos, se utilizarán como una muestra válida de las
perturbaciones aleatorias desconocidas.
2.- Antes de la aplicación de métodos técnicos (más o menos informales) debemos preguntarnos
por la existencia de heterocedasticidad desde un punto de vista teórico considerando la
naturaleza del problema analizado, las exógenas incluidas y, en definitiva, la propensión teórica
del modelo hacia la heterocedasticidad.
A. Contrastes Gráficos
A.1) Gráfica del error a través de las distintas observaciones del modelo
Dado que las series económicas presentan casi siempre una tendencia definida (positiva o
negativa), la simple gráfica de error puede servir para conocer intuitivamente si el mero
transcurso del tiempo da lugar a un incremento/decremento continuado del error, lo que sería
significativo de una relación entre la evolución de las variables del modelo y los valores cada
vez mayores o cada vez menores de éste.
Gráficos del error sintomáticos de presencia de heterocedasticidad
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
8
19
17
15
13
11
9
19
17
15
13
11
9
7
5
3
1
-10
7
-5
5
0
3
5
1
6
4
2
0
-2
-4
-6
10
En ambos, la mera evolución del tiempo está correlacionada con valores cada vez mayores
(izquierda) del error o cada vez menores (derecha), con lo que el cálculo de la varianza por
subperíodos arrojaría valores significativamente diferentes; es decir la serie del error sería
heterocedástica. Evidentemente, este tipo de gráficos SÓLO tiene sentido si el modelo es
temporal ya que, en el caso del modelo transversal, la ordenación de valores del eje “X”
dependerá del criterio elegido para ordenar la muestra, un criterio que puede no coincidir con el
patrón de crecimiento o decrecimiento de la varianza.
A.2) Gráfica del valor cuadrático del error y los valores de “Y” y “X’s”
La representación de los valores del error al cuadrado6 y la variable endógena o cada una de las
variables exógenas puede revelar la existencia de algún patrón sistemático en la varianza de la
perturbación (se entiende que el error al cuadrado se asocia con la dispersión del error). Este
tipo de gráfico, no sólo permite obtener una idea preliminar de si existe o no heterocedasticidad
sino también de la o las variables que pudieran estar conectadas con la misma.
B. Contrastes numéricos
Todos los procedimientos presentados aquí tratan de cuantificar la presencia de
heterocedasticidad. Algunos de ellos, no sólo se limitan a cuantificarla sino que, además,
permiten valorar la existencia de heterocedasticidad en términos de probabilidad recurriendo a
distribuciones estadísticas conocidas; este último grupo de contrates se denominan, por ello,
contrastes "paramétricos". 7
B.1.) Contraste de Glesjer
De forma similar al caso anterior, Glesjer propone descartar la variación del error en función de
una variable z, que ahora pueden estar elevadas a una potencia "h" que estaría comprendida
entre -1 y 1. El modelo que se propone es:
1. Estimar el modelo inicial, sobre el que se pretende saber si hay o no heterocedasticidad,
empleando MCO y determinando los errores.
6
7
Eventualmente podrían también realizarse los gráficos con valores absolutos del residuo.
En particular, los contrastes que se presentan parten de una estructura acorde a la del Multiplicador de Lagrange. De
forma muy intuitiva, sin querer hacer una argumentación estrictamente académica, diremos que en este tipo de
contrastes se propone siempre dos modelos, uno inicial y otro en el que se incorpora algún añadido en la
especificación. A partir de un ratio sobre los errores de cada uno de estos modelos (o alguna transformada de estos),
se compara si el modelo más completo aporta suficiente explicación adicional de la endógena como para compensar
el coste de incorporar más variables.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
9
yi = β 0 + β1 x1i + β 2 x2i + ... + β k xki + ui
βˆ = [X ' X ]−1 X ' Y
ei = yi − yˆ i
2. Estimar cuatro regresiones para los valores absolutos del error del modelo anterior en
función de una variable elevada consecutivamente a "h", que para cada modelo tomaría
los valores -1, -0,5, 0,5 y 1.
| ei |= α 0 + α1 z h ε i
h{− 1,−0.5,0.5,1}
Se escogerá la regresión de las cuatro con parámetros significativos y con mayor R2.
3. Se entiende que, si el valor de esta R2 es suficientemente grande, se estará confirmando
que existe heterocedasticidad producida por la variable z, ya que esta es capaz de
explicar la evolución de la evolución del error como estimada de la evolución de las
perturbaciones aleatorias. Esta conclusión es especialmente válida para muestras
grandes según las propias conclusiones ofrecidas por Glesjer por lo que su utilización
parece especialmente adecuada en este tipo de condiciones muestrales.
B.2.) Contraste de Breusch-Pagan
La idea del contraste es comprobar si se puede encontrar un conjunto de variables Z que sirvan
para explicar la evolución de la varianza de las perturbaciones aleatorias, estimada ésta a partir
del cuadrado de los errores del modelo inicial sobre el que se pretende comprobar si existe o no
heterocedasticidad.
El proceso a seguir para llevar a cabo este contraste es el siguiente:
1. Estimar el modelo inicial, sobre el que se pretende saber si hay o no heterocedasticidad,
empleando MCO y determinando los errores.
yi = β 0 + β1 x1i + β 2 x2i + ... + β k xki + ui
βˆ = [X ' X ]−1 X ' Y
ei = yi − yˆ i
2. Calcular una serie con los errores del modelo anterior al cuadrado estandarizados:
e2
e~i 2 = i 2
σˆ
e' e
σˆ 2 =
n
3. Estimas una regresión del error calculado en el paso (2) explicado por una constante y
el conjunto de las variables Z que se pretende saber si producen o no heterocedasticidad
en el modelo, obteniéndose la R2 de este modelo y la varianza de la estimada:
~
ei2 = α 0 + α1 z1i + α 2 z 2 i + ... + α p z pi + ε i
Re~2
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
10
4. En principio, dado que el modelo tiene término constante, se cumple la regla general de
las regresiones según la cual la varianza de la endógena real es igual a la suma de la
varianza de la endógena estimada más la varianza del error obtenido en el modelo
2
2
2
( S e~ 2 = S e~ˆ 2 + Sεˆ ) o su equivalente multiplicando a ambos lados de la igualdad por el
número de observaciones “n”, donde en vez de varianzas hablaremos de Sumas al
cuadrado. Por ello, si el modelo es "malo" la varianza de la endógena estimada será
pequeña (es lo mismo que decir que la varianza del error estimado es grande o que el
"modelo tiene mucho error"). En definitiva, y siguiendo el interés que aquí buscamos, si
la varianza de la endógena estimada en este segundo modelo es muy pequeña,
estaremos afirmando que el poder explicativo del conjunto de variables Z sobre la
representación de la varianza de las perturbaciones aleatorias es escaso. A partir de esta
afirmación, podríamos generar un contraste calculado con la suma residual, a sabiendas
de que cuanto más cerca de cero se encuentre, más probabilidades de homocedasticidad
habrá en el modelo. El contraste propuesto es:
S e~ˆ22 * n
2
los autores demuestran que, en el caso de un modelo homocedástico, se distribuye como
2
una χ p , con lo que, si el valor del ratio supera al valor de tablas, se rechaza la hipótesis
nula (homocedasticidad); es decir, se acepta que el conjunto de variables Z está
produciendo heterocedasticidad en el modelo original.
El contraste de Breusch Pagan efectivamente nos servirá para aceptar o descartar la presencia de
heterocedasticidad debida a ese conjunto de variables Z citado, pero su operatividad es limitada.
Si el conjunto de las variables Z contiene variables no incluidas en el modelo original, parece
difícil no haberlas tenido en cuenta antes para realizar una buena especificación y sí tenerlas en
cuenta ahora para la contrastación. Por otro lado, la lista de variables Z debe ser necesariamente
pequeña para poder realizarse el contraste.
B.3.) Contraste de White (prueba general de heterocedasticidad de White)
Aunque en apariencia esta prueba es parecida a las mencionadas anteriormente, parece admitido
que algo más robusta al no requerir supuestos previos como, por ejemplo, la normalidad de las
perturbaciones. Por otro lado, tal y como se verá a continuación, la prueba no exigirá determinar
a priori las variables explicativas de la heterocedasticidad (lo cual no es necesariamente una
virtud) y es por esta razón por lo que se denomina “prueba general”.
En este contraste la idea subyacente es determinar si las variables explicativas del modelo, sus
cuadrados y todos sus cruces posibles no repetidos sirven para determinar la evolución del error
al cuadrado. Es decir; si la evolución de las variables explicativas y de sus varianzas y
covarianzas son significativas para determinar el valor de la varianza muestral de los errores,
entendida ésta como una estimación de las varianzas de las perturbaciones aleatorias.
El proceso a seguir para realizar este contraste sería el siguiente:
1. Estimar el modelo original por MCO, determinando la serie de los errores. Escrito esto
en forma matricial para un modelo con "n" observaciones y "k" variables explicativas:
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
11
Y = Xβ + U
βˆ = [X ' X ]−1 X ' Y
Yˆ = Xβˆ
e = Y − Yˆ
2. Estimar un modelo en el que la endógena sería los valores al cuadrado de los errores
obtenidos previamente (paso 1) con todas las variables explicativas del modelo inicial,
sus cuadrados y sus combinaciones no repetidas.
ei2 = α 0 + α 1 x1i + ... + α k x ki + α k +1 x12i + ... + α k + k xki2 + α k + k +1 x1i x 2i +
α k +k +2 x1i x3i + ... + α 3k +1 x 2i x3i + ... + ε i
3. El valor de la Re2 de este segundo modelo (paso 2) nos dirá si las variables elegidas
sirven o no para estimar la evolución variante del error al cuadrado, representativo de la
varianza estimada de las perturbaciones aleatorias. Evidentemente, si la varianza de
éstas fuera constante (homocedasticidad), el carácter no constante de las variables
explicativas implicadas en el modelo no serviría para explicar la endógena, luego la Re2
debiera ser muy pequeña.
En principio, la Re2 , como proporción de la varianza de la endógena real8 que queda explicada
por la estimada, debiera ser muy pequeña si la capacidad explicativa de los regresores
considerados también es muy pequeña, siendo estos regresores, por su construcción,
representativos de varianzas y covarianzas de todas las explicativas del modelo original. Dicho
esto, evidentemente un valor de la R2 suficientemente pequeño servirá para concluir que no
existe heterocedasticidad en el modelo producida por los valores de las explicativas
consideradas en el modelo inicial. Para encontrar el valor crítico en esa consideración de
“suficientemente pequeño” se emplea la expresión deducida por Breusch y Pagan como
producto del coeficiente R2 por el número de datos del modelo, que se distribuiría del siguiente
modo:
n·Re2 → χ p −1
En definitiva, si obtenemos un valor del producto n·Re2 mayor que el reflejado por las tablas de
χ p2 −1 , afirmaremos que existe heterocedasticidad, y viceversa, si este valor es más pequeño
diremos que se mantiene la homocedasticidad (luego la hipótesis nula de este contraste es la
homocedasticidad).
Otro modo de contrastar la existencia de heterocedasticidad en el modelo a partir de la validez o
no de los parámetros incluidos en la regresión propuesta por White vendría dado por el valor del
contraste de significación conjunta F. Si dicho contraste afirmara que, en conjunto, las variables
explicitadas tienen capacidad explicativa sobre la endógena, estaríamos afirmando la presencia
de heterocedasticidad en el modelo.
8
En este caso, la endógena real será el valor del error muestral al cuadrado de la primera regresión practicada. En el
caso de homocedasticidad, este debe ser casi constante, por lo que difícilmente la evolución de otras variables podría
explicar un valor fijo. Por ello es intuitivo pensar que cuanto mayor sea la R2 de este modelo, más probable será la
heterocedasticidad.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
12
B.4.) Contraste a partir del coeficiente de correlación por rangos de Spearman
La filosofía de este contraste reside en que la variable sospechosa de producir
heterocedasticidad debería provocar un crecimiento del residuo estimado al mismo ritmo que
ella va creciendo. Por ello, si ordenáramos de menor a mayor tanto la variable “sospechosa”, por
ejemplo xji, como el valor absoluto del residuo, |ei|, el cambio de puesto en ambas, y para cada
una de las observaciones, debiera ser del mismo número de puestos respecto al orden original de
las series. En la medida en la que este cambio de puesto respecto al original no sea el mismo
para las dos (una vez ordenadas) se podría hablar de movimientos no correlacionados. Dado que
la correlación se mide entre uno y menos uno, Spearman propone determinar un grado de
correlación en ese “cambio de puesto respecto al inicial” de cada una de las variables a partir de
la diferencia entre el nuevo puesto y el inicial:
n
r =1−
6∑ d i2
i =1
n(n 2 − 1)
En esta expresión, una coincidencia máxima (todas las distancias son igual a cero), daría lugar a
una correlación de Spearman igual a uno; mientras que una distancia máxima, provocaría un
valor cero de dicho coeficiente de correlación9.
En la siguiente tabla se hace un pequeño ejemplo numérico de cálculo del coeficiente de
Spearman para clarificar lo dicho hasta ahora.
Series originales
Puesto
xji
|ei|
xji
1
2
3
4
5
1.838
424
501
2.332
688
1,6
1,4
1,2
1,3
1,5
424
501
688
1.838
2.332
Series ordenadas
Puesto
|ei|
original
2
1,2
3
1,3
5
1,4
1
1,5
4
1,6
Puesto
original
3
4
2
5
1
d
d2
2-3=-1
3-4=-1
5-2=3
1-5=-4
4-1=3
1
1
9
16
9
n
r =1−
6∑ d i2
i =1
2
n(n − 1)
=1−
6 * 30
= 1 − 1,8 = −0,8
5(25 − 1)
En este caso, el grado de correlación negativa de ambas series sería bastante elevado, dado que
los extremos de correlación serían +/-1.
Para valorar la significatividad o no de esta correlación, se conoce la función de distribución del
siguiente ratio bajo la hipótesis nula de no significatividad, demostrado por el autor:
9
Realmente, el coeficiente de correlación por rangos de Spearman es equivalente a emplear el coeficiente
de correlación lineal
r ( x, y ) =
cov( x, y )
a las variables de puntuación de orden de ambas colocadas
SxS y
según la progresión de una de ellas. Para ver el detalle del denominador, se puede acudir a MartínGuzmán y Martín Pliego (1985), páginas 312-314.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
rs N − 2
1 − rS2
13
→ t n −2
Con ello, si el resultado del ratio es superior al valor de tablas podremos afirmar que la
correlación es significativa o, de cara a nuestro interés en este caso, que hay indicios de
heterocedasticidad en el modelo provocada por la variable xji.
B.5) Otros contrastes
Aunque no se comentarán aquí, si es conveniente citar otros contrastes habituales para la
determinación de la heterocedasticidad, como:
-
Contraste de Harvey
Contraste test de Park
Contraste RESET de Ramsey
Golfeld-Quandt
Contraste de picos
LM Arch
5.- Cómo se corrige
Antes de entrar en los métodos operativos que permiten la estimación en presencia de
heterocedasticidad, deben hacerse dos puntualizaciones:
1.- La corrección que se verá en este apartado se plantea como una estrategia adaptativa, de
convivencia con la heterocedasticidad pero, en todo caso, debe entenderse que, en algunas
ocasiones, el problema que genera un comportamiento heterocedástico de la perturbación puede
resolverse variando la especificación lo que, sin duda alguna, sería una verdadera corrección del
problema.
2.- La estimación alternativa al uso de MCO en situaciones de heterocedasticidad es la
utilización de MCG y, por tanto, esta es la única estrategia analíticamente correcta para la
solución del problema. No obstante, y como ya se ha dicho, esto implicaría conocer el verdadero
valor de la matriz sigma de varianzas y covarianzas, situación que, en la práctica, no es habitual.
Por tanto, los métodos que se presentan aquí suponen una alternativa operativa a esta hipotética
situación ideal.
1.- Transformación de las variables originales
Como hemos venido viendo repetidas veces a lo largo del tema, la heterocedasticidad viene
producida por la dependencia de la varianza de las perturbaciones aleatorias de una o más
variables que, a su vez, pueden estar presentes en el modelo o no. Los distintos métodos de
detectar este problema servían para probar la dependencia de la varianza de la perturbación
aleatoria de un conjunto de variables, a partir de lo que hemos llamado un supuesto
simplificador:
σ i2 = f (σ 2 Z i )
Por lógica, el modo de subsanar el problema detectado será operar convenientemente la
variables del modelo precisamente eliminando la fuente de heterocedasticidad que habremos
podido definir cuando detectamos la misma. Como veremos a continuación, si el conjunto total
de las variables del modelo (endógena incluida) es dividido por la forma estimada de esta
función de la raíz de la varianza heterocedástica (una vez algún método de detección nos haya
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
14
confirmado que efectivamente el comportamiento de esta varianza se puede seguir
convenientemente con dicha función) estaremos corrigiendo el modelo.
Para comprobar esto, podemos volver a la forma matricial de varianzas covarianzas no escalar:
 E (u1 ) 2
.   E (u1 ) 2

 
E (u1u 2 ) E (u 2 ) 2
= 0
E (UU ' ) = 

  0
...

 
E (u n ) 2   0
 E (u1u n ) E (u 2 u n )


 = σ 2 I = σ 2Σ
i n

...

0 E (u n ) 2 
.
E (u 2 )
0
0
2
En esta matriz, si dividimos por σ i = f (σ Z i ) , obtendremos una diagonal principal de unos;
2
2
es decir, volveríamos al caso de una matriz de varianzas covarianzas escalar tal y como la que se
supone en el modelo básico de regresión lineal.
Formalmente, para probar esto seguimos los siguientes pasos. Dado que la matriz Σ es una
matriz semidefinida positiva (todos los elementos de su diagonal principal son necesariamente
positivos), siempre podremos descomponerla en dos matrices de la forma:
Σ = PP ' ⇔ Σ −1 = P −1 P −1 '
Volviendo a la matriz de varianzas covarianzas no escalar y uniendo esto a la función que
2
2
hemos comprobado sirve para definir esta varianza no constante σ i = f (σ Z i ) , es fácil llegar
a que la descomposición Σ = PP ' ⇔ Σ −1 = P −1 P −1 ' es:
 E (u1 ) 2

 0
 0

 0
σ 1

0
0

 0
σ2
0
0
 σ 1 2
 
2
 =  0 σ2
  0
...
0

2
0 E (u n )   0
0
.
E (u 2 )
2
0
0
. 



...

0 σ n 
'
σ 1

0
0

 0
σ2
0
0
. 

 = σ 2Σ =

...
2
0 σ n 
. 

 = σ 2 PP'

...

0 σ n 
Si multiplicamos cada variable del modelo por esta matriz P, tal y como se ha sugerido,
obtenemos unas nuevas variables del siguiente tipo:
P −1Y = P −1 xβ + P −1U ⇔ Y * = X * β + U *
donde:
E (UU ' ) = σ 2 Σ 
E (U *U * ' ) = E ( P −1UU ' P −1 ' ) = P −1 P −1 ' E (UU ' ) =  −1 −1
= Σ −1σ 2 Σ = σ 2 I n
−1 
P
P
'
=
Σ


Por lo que podemos afirmar que el modelo transformado (aquel por el que se han dividido todas
las variables por la desviación típica estimada de las perturbaciones aleatorias) soporta una
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
15
matriz de varianzas covarianzas de las perturbaciones aleatorias escalar, con lo que se puede
estimar con toda garantía por MCO.
En definitiva, y a modo de breve “receta”, los pasos para la corrección de la heterocedasticidad
serían los siguientes:
a) Se estiman los parámetros del modelo por MCO, ignorando por el momento el
problema de la heterocedasticidad de las perturbaciones aleatorias
b) Se establece un supuesto acerca de la formación de σ i2 y se emplean los residuos de la
regresión por MCO para estimar la forma funcional supuesta.
c) Se divide cada observación por σˆ i2 según el paso anterior (según el valor de esa
heterocedasticidad supuesta estimada, siempre y cuando un contraste nos haya
confirmado que el “modelo simplificador” es bueno).
d) Se estima el modelo original ahora con todas las variables transformadas según el paso
c).
2.- Estimación consistente de White
El procedimiento propuesto por White permite una estimación que, en términos asintóticos,
permite la utilización de los procedimientos de inferencia estadística clásica.
Básicamente, la idea consiste en utilizar los errores cuadráticos de una estimación previa de
MCO como elementos de la matriz de varianzas de la perturbación (matriz Σ). White demostró
que, esta estrategia de “ponderación” permite obtener estimadores consistentes de las varianzas
de los parámetros. La mayor parte de los paquetes informáticos incorporan este cálculo de modo
que, en general, su utilización parece recomendable, al menos con fines exploratorios.
En todo caso, deben hacerse dos puntualizaciones que quizá resulten interesantes al que, por vez
primera, se asome a este procedimiento.
1.- Los parámetros estimados consistentemente con White coincidirán con los de la regresión
original MCO (en todo caso, recuerde que el problema de la heterocedasticidad no es un
problema de sesgo ni inconsistencia).
2.- Nada garantiza, a priori, que las varianzas de los parámetros estimados con White sean
menores que las originales, dado que debe recordarse que las MCO originales (mal calculadas)
presentaban un sesgo indeterminado, pero generalmente de infravaloración de la varianza real.
TRATAMIENTO DE LA HETEROCEDASTICIDAD EN E-VIEWS
Se propone un modelo para cuantificar las ventas de Burger King (VTASBK) en una serie de 20
países, proponiéndose como explicativas las siguientes variables:
PRECIOSBK:
PRECIOSMAC:
RENTAPC:
Precios Hamburguesa Whoper
Precios Hamburguesa Big Mac
Renta per capita del país
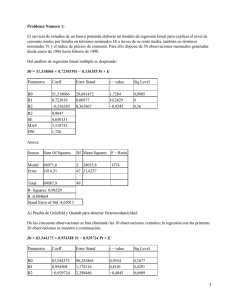
Realizada una primera regresión, los resultados obtenidos son los siguientes:
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
16
1000
800
600
400
20
200
10
0
0
-10
-20
-30
2
4
6
Residual
8
10
12
Actual
14
16
18
20
Fitted
Matriz de correlaciones de las variables
VTASBK
PRECIOSBK
PRECIOSMAC
RENTA PC
VTASBK
1.000000
0.360900
0.226085
0.999566
PRECIOSBK PRECIOSMAC
0.360900
0.226085
1.000000
0.704328
0.704328
1.000000
0.367945
0.235402
RENTAPC
0.999566
0.367945
0.235402
1.000000
No se da ninguna correlación entre variables explicativas superior al R2 obtenido en el modelo,
por lo que no parece haber indicios de multicolinealidad. Tan sólo existe una fuerte correlación
entre PRECIOSBK y PRECIOSMAC (0,7043), en cualquier caso más pequeño que el 0,99.
A la luz del gráfico de residuos, podría pensarse que que los cinco primeros países presentarían
una varianza mayor que los siguientes, aunque, como suele ocurrir con los gráficos, no se puede
apreciar nada claramente.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
17
El siguiente elemento a contrastar sería la presencia de heterocedasticidad en el modelo. El
programa E-Views suministra, con este fin, la posibilidad de detectar la heterocedasticidad,
entre otros, a partir del Test de Residuos de White, ofreciendo dos posibilidades:
-
-
No Cross Terms: Realizar la regresión de los errores al cuadrado de la regresión inicial
del modelo escribiendo como explicativas todas las exógenas de la inicial y sus valores
al cuadrado.
Cross Terms: igual que la anterior, pero incluyendo además, como explictivas del error
al cuadrado, los productos no repetidos de todas las variables explicativas del modelo
inicial entre sí.
En principio, el contraste expresado por White sería la segunda opción, pero, en modelos con
escasas observaciones, a lo mejor no es posible realizar la estimación con tantos regresores y es
más recomendable la primera opción (por no eliminar completamente los grados de libertad).
En nuestro caso, el número de observaciones es 20 (países) y el número de explicativas tres más
la constante, luego el contraste de White con términos cruzados equivaldría a incluir 10
variables explicativas sobre el cuadrado de los errores de la regresión inicial (la constante, las
tres explicativas, sus tres cuadrados y los tres cruces posibles no repetidos entre ellas).
Para aplicar este contraste en E-views, desde la misma ventana donde se ha realizado la
regresión, se sigue el siguiente trayecto:
Los resultado de este Test de residuos White heteroskedasticity (cross terms) son:
White Heteroskedasticity Test:
F-statistic
Obs*R-squared
7.458779
17.40694
Probability
Probability
0.002102
0.042712
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
18
Como resultado, se nos ofrecen dos formas de contrastar la validez de las variables elegidas para
explicar un comportamiento no homogéneo del error al cuadrado (estimador de la varianza de la
perturbación aleatoria en este caso):
-
F-stastitic (como siempre con k-1; n-k grados de libertad), nos vendría a dar una medida
de la bondad del modelo (probabilidad de heterocedasticidad si se confirma la validez
conjunta de las variables elegidas para determinar la variación del error al cuadrado - la
endógena-).
-
Obs*R-squared ( n·Re2 → χ p −1 ): supuesta la hipótesis nula de homocedasticidad, el
cálculo propuesto debería comportarse como una χ p −1 con p-1 grados de libertad. En
nuestro caso p=10 (las explicativas de la regresión practicada). (El valor de tablas de
χ 102 −1 , para el 95% de confianza, es 16,9).
A la luz de lo dicho, ambos estadísticos propuestos afirman, con un 97,9% de probabilidades el
primero y con un 96,73% de probabilidades el segundo, la existencia de heterocedasticidad.
La misma salida nos muestra la regresión utilizada para realizar estos cálculos, que sería la
siguiente:
Test Equation:
Dependent Variable: RESID^2
Method: Least Squares
Date: 04/04/01 Time: 18:13
Sample: 1 20
Included observations: 20
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
PRECIOSBK
PRECIOSBK^2
PRECIOSBK*PRECIOSMAC
PRECIOSBK*RENTAPC
PRECIOSMAC
PRECIOSMAC^2
PRECIOSMAC*RENTAPC
RENTAPC
RENTAPC^2
-1244.796
-3872.145
1071.919
-423.3863
0.065588
6562.125
-2332.049
0.048495
-0.090230
-7.94E-07
761.4100
4225.294
452.8574
3433.568
0.019299
4306.578
3209.945
0.039574
0.034504
2.13E-07
-1.634856
-0.916420
2.367012
-0.123308
3.398529
1.523745
-0.726507
1.225423
-2.615066
-3.719294
0.1331
0.3810
0.0395
0.9043
0.0068
0.1586
0.4842
0.2485
0.0258
0.0040
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.870347
0.753659
51.71438
26743.77
-100.3620
1.810789
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
57.08155
104.1942
11.03620
11.53407
7.458779
0.002102
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
19
A la luz de esta regresión, es fácil comprobar la significatividad de la variable rentapc y
rentapc^2 para explicar la varianza del error. También los es preciosbk^2 y preciosbk*rentapc.
Para corregir el problema de la heterocedasticidad, habría que emplear Mínimos Cuadrados
Generalizados, o bien transformar todas las variables del modelo predividiendo todas sus
observaciones por la raíz cuadrada del valor estimado del error al cuadrado en el modelo que se
ha utilizado para contrastar la presencia de heterocedasticidad y que nos ha informado sobre la
presencia de la misma y la buena explicación del comportamiento no constante de la varianza.
El programa E-views permite realizar la estimación por MCG usando como valor de Σ el
obtenible a partir de la propuesta de White (1980).
El estimador consistente de la matriz de covarianzas para lograr una estimación correcta de los
parámetros en presencia de heterocedasticidad es el siguiente:
Σˆ =
n
n
[X ' X ]−1  ∑ eit2 x't xt [X ' X ]−1
n−k
 i =1

Para lograr una estimación empleando esta corrección en E-views, es necesario, una vez se
ejecuta una estimación lineal normal, pulsar el botón de “estimate”. Aparecerá entonces, a la
derecha, un botón de opciones que, pulsado, permite señalar “Heteroskedasticity: consistent
covariance White”.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
20
Estimando según esta propuesta, ya que hemos confirmado la presencia de heterocedasticidad,
los resultados serían los siguientes:
Dependent Variable: VTASBK
Method: Least Squares
Date: 04/20/01 Time: 13:37
Sample: 1 20
Included observations: 20
White Heteroskedasticity-Consistent Standard Errors & Covariance
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
PRECIOSBK
PRECIOSMAC
RENTAPC
23.78791
-2.356251
-16.74075
0.025278
8.785312
7.695290
13.70312
0.000213
2.707691
-0.306194
-1.221674
118.6913
0.0155
0.7634
0.2395
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.999224
0.999078
8.447007
1141.631
-68.82358
2.376763
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
421.8983
278.2593
7.282358
7.481504
6867.346
0.000000
Referencias bibliográficas
GUJARATI, D. (2006): Principios de Econometría. Mc Graw Hill, Capítulo 13. pag.385
GOLFEDLD,SM Y QUANDT (1972): Non Linnear Methods in Econometrics. North Holland,
pag. 280.
MARTÍN-GUZMÁN Y MARTÍN PLIEGO (1985): Curso básico de Estadística
Económica. Editorial AC
NOVALES, A. (1993): Econometría. Editorial M'c Graw Hill, segunda edición. Madrid.
Capítulo 6, página: 193.
OTERO, JM (1993): Econometría. Series temporales y predicción. Editorial AC, libros
científicos y técnicos. Madrid.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
21
PULIDO, A. y PÉREZ, J. (2001): Modelos Econométricos. Editorial Pirámide, SA. Madrid.
Capítulo 14, página: 711.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
22
Ejemplo práctico de análisis de heterocedasticidad
Ramón Mahía – Marzo 2006
I.- REGRESIÓN INICIAL
Los datos para realizar esta regresión se han tomado del ejemplo 11.10 del libro
“Econometría” de D.N. Gujarati, Ed. Mc.Graw Hill. Cuarta Edición. Los datos se
refieren a gastos en I+D (GID), Ventas y Beneficios para 18 sectores industriales
considerados y fueron a su vez extraídos de Business Week, Special 1989 Bonus Issue,
R&D Scorecard, pp. 180-224. .
El ejemplo utilizado no se corresponde, sin embargo, con el realizado por Gujarati en el
texto arriba indicado: la regresión que se propone para el análisis en este ejemplo trata
de explicar los cambios en los gastos en I+D en función de las ventas y los beneficios.
I.A.- Output de la Estimación
Dependent Variable: GID
Method: Least Squares
Date: 03/02/06 Time: 11:36
Sample: 1 18
Included observations: 18
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
VENTAS
BENEFICIOS
-139.3921
0.012558
0.239862
9920.038
0.017998
0.198594
-0.014052
0.697731
1.207801
0.9890
0.4960
0.2458
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.524535
0.461139
27204.69
1.11E+10
-207.7006
3.173929
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
30568.83
37060.02
23.41118
23.55957
8.274023
0.003788
3 apuntes muy breves sobre la valoración global de signos y significación:
-
Signos correctos
Variables no significativas ni individualmente ni de forma conjunta
R2 escaso
I.B.- ¿Problemas de multicolinealidad?
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
23
A la vista de la fuerte correlación entre ventas y beneficios, lo más probable es que SI.
No obstante, vamos a mantener la regresión sin cambios con estas dos explicativas con
el fin de ilustrar los procedimientos de detección de heterocedasticidad en este contexto
multivariante.
II.- DETECCIÓN DE LA HETEROCEDASTICIDAD
II.B.- Aproximación Teórica
La utilización de modelos transversales, especialmente cuando las unidades observadas
presentan, para las variables de interés, diferentes tamaños, supone un riesgo evidente
de heterocedasticidad. Por otro lado, cabe suponer que los gastos en I+D sean, no sólo
más grandes cuanto mayor sea la empresa (mayor sea su volumen de ventas), sino
probablemente también más variables; algo similar ocurre de hecho con otras variables
empresariales que presentan una distribución heterocedástica respecto al tamaño (la
distribución de salarios, la productividad, … etc.).
II.B.- Aproximación Gráfica
II.B.1.- Real, estimada, error.
La muestra aparece ordenada según el tamaño (ventas) de la empresa. Por ello, y a pesar
de tratarse de un modelo transversal, este tipo de gráfico tiene sentido en este ejemplo si
suponemos que la heterocedasticidad está relacionada con el tamaño .
150000
100000
50000
100000
0
50000
0
-50000
-100000
2
4
6
Residual
8
10
12
Actual
14
16
Fitted
18
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
24
El gráfico de los errores muestra, efectivamente, que la dispersión de los mismos
alrededor de la media nula aumenta según el tamaño de la empresa también lo hace (en
este caso, insisto, el eje horizontal no representa sólo la transición de unas empresas a
otras sino también el incremento de tamaño dado que la muestra aparece ordenada por
volumen de ventas).
II.B.2.- Gráficos X/Y (“scat”) entre errores y variables
La representación de los residuos al cuadrado de la regresión y la variable de ventas o
beneficios (amabas representan el tamaño), arroja, nuevamente un claro indicio de
relación entre ambas. Se ilustran dos versiones de los mismos gráficos, en la primera
versión se ha utilizado la muestra completa de errores, en la segunda, con el fin de
acentuar el gráfico, se han eliminado los dos residuos atípicamente grandes de la serie
de errores cuadráticos (observaciones 16 y 17). En todos los casos se muestra la línea de
regresión de la nube de puntos en la que se aprecia, claramente, una pendiente positiva.
La utilización de residuos en valor absoluto en lugar de residuos cuadráticos no implica
diferencias sustanciales.
Gráficos Errores Cuadráticos / Exógenas (sin corrección de atípicos)
5.E+09
RESID2
4.E+09
3.E+09
2.E+09
1.E+09
0.E+00
0
1000000
2000000
VENTAS
3000000
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
25
5.E+09
RESID2
4.E+09
3.E+09
2.E+09
1.E+09
0.E+00
0
50000 100000 150000 200000 250000
BENEFICIOS
Gráficos Errores Cuadráticos / Exógenas (corregidos atípicos observaciones 16 y 17)
8.E+08
RESID_AT
6.E+08
4.E+08
2.E+08
0.E+00
0
1000000
2000000
VENTAS
3000000
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
26
8.E+08
RESID_AT
6.E+08
4.E+08
2.E+08
0.E+00
0
50000 100000 150000 200000 250000
BENEFICIOS
II.C.- Métodos numéricos
II.C.1.- Regresiones univariantes de Glesjer
Conforme al procedimiento descrito en los documentos teóricos, realizamos la
estimación del valor absoluto del residuo en función de cada una de las dos exógenas
utilizando distintas parametrizaciones para el modelo (distintos valores de “h”).
ei = β 0 + β1 X ih + vi
Para estas regresiones, observamos el valor del coeficiente de determinación R2 y el “pvalue” del contraste “t” de Student para el coeficiente β1.
2
h=0,5
h=1
h=2
h=-0.5
h=-1
h=-2
R
0.57
0.63
0.68
0.25
0.17
0.13
Beneficios
p-value
0.0004
0.0001
0.0000
0.0358
0.0862
0.1392
2
R
0.46
0.42
0.27
0.33
0.23
0.11
Ventas
p-value
0.0019
0.0034
0.0280
0.0123
0.0461
0.1842
A la vista de los resultados, se confirma la evidente relación del error con las variables
exógenas, especialmente con la variable de beneficios. La parametrización con mejores
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
27
resultados (la que en mayor medida evidencia la heterocedasticidad) supone la relación
entre los errores absolutos y el beneficio al cuadrado lo cual puede ser d einterés a la
hora de proponer una transformación homocedástica para el modelo.
II.C.2.- Contraste de Breusch - Pagan
Realizamos en primer lugar la transformación de la serie de residuos originales RGID a
la versión cuadrática estandarizada que se propone en el contraste BP:
2
e
~
ei = i
σ e2
Para realizar este cálculo, primero necesitamos conocer el valor de la varianza residual
de los residuos originales que resulta ser:
σ
2
e
∑e
=
2
i
n
=
11.101.429.732,93
= 616.746.096,27
18
de modo que tenemos10:
RGID
ei
-480,17
-4.156,22
-581,86
-6.806,36
1.228,31
-2.099,32
5.018,89
-11.846,96
-15.734,91
22.961,39
16.594,31
-21.285,29
25.552,56
-10.109,80
-9.424,18
62.836,05
-66.054,61
14.388,17
RGID_2ST
ei2
σ e2
0,0004
0,0280
0,0005
0,0751
0,0024
0,0071
0,0408
0,2276
0,4014
0,8549
0,4465
0,7346
1,0587
0,1657
0,1440
6,4019
7,0746
0,3357
Realizamos ahora la regresión de esta serie de residuos transformada en función de
la/las variables aparentemente conectadas con la heterocedasticidad. En nuestro caso,
proponemos utilizar el beneficio y su cuadrado como variables explicativas:
2
~
ei = β 0 + β1 ⋅ (BENEFICIOS )i + β 2 ⋅ (BENEFICIOS )i + vi
10
En E-Views, si nuestra variable original de residuos se denomina RGID, la variable
transformada para BP podría generarse como: rgid_2st=(rgid/(@var(rgid))^0.5)^2
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
28
Dependent Variable: RGID_2ST
Method: Least Squares
Date: 03/02/06 Time: 13:02
Sample: 1 18
Included observations: 18
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
BENEFICIOS
BENEFICIOS^2
0.544613
-2.62E-05
2.23E-10
0.586361
1.54E-05
7.09E-11
0.928802
-1.698895
3.144029
0.3677
0.1100
0.0067
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.699449
0.659376
1.234069
22.84389
-27.68570
1.798649
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
1.000000
2.114471
3.409522
3.557918
17.45420
0.000121
La suma cuadrática explicada de esta regresión es
∑ e~ˆ
2
i
= 56.2901
es decir:
∑ e~ˆ
i
2
2
= 28.14500503
Con el fin de contrastar la Hipótesis nula de nula de Homocedasticidad, y dado que la
ratio SCE/2 se distribuye como una Chi cuadrado con “p” grados de libertad (número de
parámetros estimados) observamos el valor de una Chi cuadrado a una sola cola para un
nivel de significación del 95% y 3 grados de libertad (parámetros estimados en la
regresión): 7.81. El valor muestral calculado, 26.59 es claramente superior al valor de
tablas luego, al 95% de confianza, rechazamos la hipótesis nula de Homocedasticidad.
II.C.3.- Contraste de White
No parecen necesarios contrastes adicionales para asegurar la presencia de
heterocedasticidad ligada a la variable de beneficios pero, no obstante, realizamos la
prueba de White con fines ilustrativos. E-Views realiza de forma automática este
contraste si, una vez realizada la regresión, hacemos “clic” sobre la opción ViewResidual Test – White Heteroskedasticity11.
11
La opción “cross terms” utiliza como exógenas los productos cruzados de las variables exógenas
mientras que opción “no cross terms” sólo emplea las exógenas y sus cuadrados.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
29
La regresión de White, efectuada para los residuos cuadráticos en función de las
variables exógenas, sus cuadrados y sus productos cruzados resulta ser:
White Heteroskedasticity Test:
F-statistic
Obs*R-squared
19.41756
16.01994
Probability
Probability
0.000022
0.006787
Test Equation:
Dependent Variable: RESID^2
Method: Least Squares
Date: 03/02/06 Time: 15:29
Sample: 1 18
Included observations: 18
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
VENTAS
VENTAS^2
VENTAS*BENEFICIOS
BENEFICIOS
BENEFICIOS^2
69515964
1349.794
-0.002708
0.050108
-19656.93
-0.116371
2.65E+08
1077.114
0.000790
0.020746
12978.05
0.146632
0.262044
1.253157
-3.426789
2.415348
-1.514630
-0.793626
0.7977
0.2340
0.0050
0.0326
0.1558
0.4428
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.889997
0.844162
5.15E+08
3.18E+18
-382.9592
2.127352
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
6.17E+08
1.30E+09
43.21768
43.51448
19.41756
0.000022
Una vez más, los indicios de autocorrelación son claros. Los resultados del test de
White muestran, por un lado, el elevado valor de la R2 en la regresión instrumental, que
supera el valor de una Chi cuadrado con “p-1”=”6-1” grados de libertad, para un nivel
de significación del 0.67%, es decir, del 99,3%. Por otro lado, aparecen coeficientes
estadísticamente significativos al 99,5% para la variable de “Beneficios al cuadrado” y
al 96,8% para el producto cruzado de los Beneficios por las Ventas.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
30
III.- CORRECCIÓN DE LA HETEROCEDASTICIDAD
III.A.- Transformación de las variables originales
Proponemos como solución al problema la transformación de los datos originales
utilizando para la transformación la variable de Beneficios al cuadrado, es decir, aquella
que en mayor medida se ha mostrado conectada con la heterocedasticidad.
En la práctica, eso supone dividir la endógena y las exógenas entre la variable de
beneficios (la raíz de los beneficios al cuadrado son los propios beneficios). Por
ejemplo, y para el caso de la endógena, la regresión se efectuaría ahora utilizando como
variable a explicar la ratio de los Gastos en I+D sobre los beneficios.
Pantalla de Estimación: INICIAL
Pantalla de Estimación: TRANSFORMADA
Pueden observarse los siguientes cambios que merecen atención:
1.- Al dividir todas las variables entre la variable BENEFICIOS, debemos
observar que también quedará dividida la propia variable BENEFICIOS,
generando por tanto una variable con todos sus valores iguales a “1”; es decir,
generando un término independiente. Por esa razón no se especifica en la
versión corregida de E-Views la aparición del término “C”.
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
31
2.- El término independiente de la regresión original, especificado en E-Views
originalmente como “C”, era en realidad una variable con todos sus valores
iguales a “1”. Al dividir ese término independiente entre la variable
“BENEFICIOS” tenemos en realidad una nueva variable 1/Beneficios, que es la
que aparece en la pantalla de estimación.
Esta transformación puede observarse matricialmente aquí:
Matriz Original “X” ⇒ Matriz Transformada “X”
1

1
1

 ..

 ..
1

Ventas1
Ventas 2
Ventas3
Ventas18
 1

Benef1
Benef1   1

Benef 2   Benef
2

Benef 3   1
⇒
  Benef 3
  ..
 
Benef18   ..
 1

 Benef18
Ventas1
Benef1
Ventas 2
Benef 2
Ventas3
Benef 3
Ventas18
Benef18

1


1

1





1

Dependent Variable: GID/BENEFICIOS
Method: Least Squares
Date: 03/02/06 Time: 15:58
Sample: 1 18
Included observations: 18
White Heteroskedasticity-Consistent Standard Errors & Covariance
Variable
Coefficient
Std. Error
t-Statistic
Prob.
1/BENEFICIOS
VENTAS/BENEFICIOS
BENEFICIOS/BENEFICIOS
-1269.387
0.022273
0.124798
365.6084
0.001510
0.064034
-3.471986
14.75451
1.948917
0.0034
0.0000
0.0703
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.819102
0.794982
0.225319
0.761527
2.924325
2.486807
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
0.467849
0.497624
0.008408
0.156804
33.95985
0.000003
Si se desea comparar los coeficientes de esta nueva regresión con los de la original,
podría multiplicarse toda la regresión por la variable “Beneficios”. Los parámetros de
la regresión original son ahora ligeramente distintos a los de la original, sus errores
estándar mucho más reducidos y el coeficiente de determinación ha mejorado
sustancialmente:
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
32
Regresión Inicial
-139.39
9920.038
0.9890
0.012558
0.017998
0.4960
0.239862
0.198594
0.2458
0.5245
Término Independiente
Std. Error
p-value
Ventas
Std. Error
p-value
Beneficios
Std. Error
p-value
R2
Regresión Corregida
-1269,38
365.6084
0.0034
0.022273
0.001510
0.0000
0.124798
0.064034
0.0703
0.8191
Por otro lado, la representación de los residuos de la regresión no muestra,
aparentemente, indicios de heterocedasticidad:
2.5
2.0
1.5
1.0
0.5
0.4
0.0
0.2
0.0
-0.2
-0.4
2
4
6
Residual
8
10
12
Actual
14
16
18
Fitted
III.B.- Estimación de White
El propio E-Views ofrece la posibilidad de utilizar una estimación corregida a partir de
una ponderación realizada con los residuos obtenidos del contraste de White. Esta
opción está disponible en la pantalla del menú de estimación de la ecuación, dentro de la
opción “Options”:
Conceptos básicos sobre Heterocedasticidad y Tratamiento en E-views
33
Cuando se hace esto, se obtiene para nuestro ejemplo la siguiente estimación:
Dependent Variable: GID
Method: Least Squares
Date: 03/02/06 Time: 16:14
Sample: 1 18
Included observations: 18
White Heteroskedasticity-Consistent Standard Errors & Covariance
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
VENTAS
BENEFICIOS
-139.3921
0.012558
0.239862
6783.051
0.014446
0.244817
-0.020550
0.869279
0.979758
0.9839
0.3984
0.3427
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.524535
0.461139
27204.69
1.11E+10
-207.7006
3.173929
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
30568.83
37060.02
23.41118
23.55957
8.274023
0.003788
Puede comprobarse que los parámetros obtenidos en la regresión no difieren de los
iniciales pero, sin embargo, sí lo hace su precisión (su Std. Error) y, por tanto, sus
estadísticos de significatividad individual. En nuestro caso, la precisión del parámetro
relativo a las ventas es menor si se utiliza la corrección de White mientras que sucede lo
contrario para el caso de la variable beneficios.