3. Aritmética binaria
Anuncio

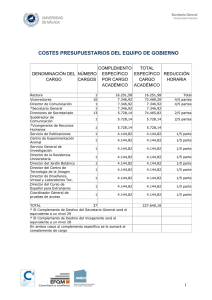
3. Aritmética binaria Oliverio J. Santana Jaria Sistemas Digitales Ingeniería Técnica en Informática de Sistemas Curso 2006 – 2007 Introducción La aritmética binaria es esencial en los ordenadores y en muchos otros tipos de sistemas digitales Para comprender los circuitos aritméticos es necesario conocer los principios básicos de estas operaciones Los objetivos de este tema son: Describir las operaciones de suma, resta, multiplicación y división de números binarios Introducir los distintos convenios usados para la representación de números negativos Detallar el proceso de realización de operaciones aritméticas en el formato más frecuentemente usado: complemento a 2 Aritmética binaria 2 1 Estructura del tema Introducción Operaciones aritméticas básicas Suma Resta Multiplicación División Representación de números enteros Signo-magnitud Complemento a 1 Complemento a 2 Resumen y bibliografía Aritmética binaria 3 Suma binaria La operación de suma se estructura en columnas El bit menos significativo del resultado de una columna es la suma de dicha columna El bit más significativo del resultado de una columna pasa como acarreo a la columna siguiente Las cuatro reglas básicas de la suma binaria son: suma 0, acarreo 0 0 + 1 = 01 suma 1, acarreo 0 1 + 0 = 01 suma 1, acarreo 0 1 + 1 = 10 suma 0, acarreo 1 0 + 0 = 00 Aritmética binaria 4 2 Suma binaria En el momento en el que aparece un acarreo igual a 1 nos vemos obligados a sumar tres bits en lugar de dos suma 1, acarreo 0 1 + 0 + 1 = 10 suma 0, acarreo 1 1 + 1 + 0 = 10 suma 0, acarreo 1 1 + 1 + 1 = 11 suma 1, acarreo 1 1 + 0 + 0 = 01 Ejemplo: 1110 + 1010 1 1 1 1 1 0 14 + 1 0 1 0 + 10 1 1 0 0 0 24 Aritmética binaria 5 Suma binaria Otro ejemplo: 1001001010’11 + 1101010111’1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 1 0 ’ 1 1 + 1 1 0 1 0 1 0 1 1 1 ’ 1 0 1 0 1 1 0 1 0 0 0 1 0 ’ 0 1 586’75 + 855’5 = 1442’25 Aritmética binaria 6 3 Resta binaria La operación de resta también se organiza en columnas Si el minuendo es menor que el sustraendo (0 menos 1) El resultado de la resta es la diferencia entre los dos Se produce un acarreo negativo, es decir, sumamos 1 al sustraendo de la siguiente columna Sumar un acarreo negativo a un 1 en el sustraendo implica la generación de un nuevo acarreo negativo Ejemplo: 1101 - 111 – 1 1 1 1 0 1 13 0 1 1 1 – 7 0 1 1 0 6 Aritmética binaria 7 Resta binaria Otro ejemplo: 1010101110’10 – 1001110100’01 1 0 1 0 1 0 1 1 1 0 ’ 1 0 1 1 1 1 – 1 0 0 1 1 1 0 1 0 0 ’ 0 1 0 0 0 0 1 1 1 0 1 0 ’ 0 1 686’5 – 628’25 = 58’25 Aritmética binaria 8 4 Multiplicación binaria Las reglas básicas de la multiplicación binaria son: 0x0=0 1x0=0 0x1=0 1x1=1 La multiplicación se realiza generando productos parciales, desplazando cada nuevo producto parcial una posición a la izquierda y luego sumándolos todos Ejemplo: 11 x 10 1 x 1 0 + 1 1 1 0 0 1 0 1 3 x 2 6 Aritmética binaria 9 Multiplicación binaria Otro ejemplo: 11010 x 101 1 1 0 1 0 x 1 0 1 1 1 1 0 1 0 0 0 0 0 0 1 1 + 1 1 0 1 0 1 0 0 0 0 0 1 0 Aritmética binaria 26 x 5 = 130 10 5 División binaria La división binaria sigue el procedimiento tradicional de multiplicación y resta al que estamos acostumbrados Ejemplo: 110 / 11 1 1 – 1 1 0 0 – 0 0 1 1 1 0 6 0 3 2 0 0 0 Aritmética binaria 11 División binaria Otro ejemplo: 100011 / 110 1 0 0 0 1 1 1 1 – 1 1 0 1 1 0 1 0 1 0 0 1 0 1 1 1 – 1 1 0 0 1 0 1 35 / 6 = 5 (resto = 5) Aritmética binaria 12 6 Estructura del tema Introducción Operaciones aritméticas básicas Suma Resta Multiplicación División Representación de números enteros Signo-magnitud Complemento a 1 Complemento a 2 Resumen y bibliografía Aritmética binaria 13 Números con signo Los sistemas digitales deben ser capaces de manejar tanto números positivos como números negativos Un número binario con signo se caracteriza por su magnitud y su signo La magnitud indica el valor del número El signo indica si es positivo o negativo Vamos a ver tres formatos binarios para representar números enteros En todos ellos, el bit más significativo representa el signo Todos los números en un ordenador tienen la mismo cantidad de bits, por lo que el bit de signo tiene una posición fija Aritmética binaria 14 7 Signo-magnitud El bit más a la izquierda representa el signo del número y el resto de bits representan la magnitud del número Un número negativo tiene los mismos bits de magnitud que su versión positiva, pero distinto bit de signo Se utiliza un 0 para el signo positivo Se utiliza un 1 para el signo negativo Dado que los números usados por un ordenador tienen tamaño fijo, supondremos números de 8 bits 26 25 24 23 22 21 20 0 0 0 1 0 1 0 1 1 0 0 1 0 1 0 1 16 + 4 + 1 21 16 + 4 + 1 –21 Aritmética binaria 15 Rango de valores en signo-magnitud Los números binarios naturales de n bits pueden tener valores que van desde 0 hasta 2n – 1 Dado que los números en formato signo-magnitud usan un bit de signo, un número de n bits sólo dedicará (n – 1) bits a representar la magnitud Los números en signo-magnitud pueden tener valores que van desde –(2n–1 – 1) hasta +(2n–1 – 1) Aritmética binaria binario decimal 000 0 001 1 010 2 011 3 100 –0 101 –1 110 –2 111 –3 16 8 Aritmética en signo-magnitud Suma y resta en signo-magnitud Se comparan el signo y la magnitud de los operandos Si el signo de los operandos es el mismo se suman las magnitudes y se mantiene el mismo signo Si el signo de los operandos es distinto, se resta la magnitud mayor menos la menor y se pone el signo de la mayor Multiplicación y división en signo-magnitud: Se multiplican o dividen las magnitudes Si los operandos tienen el mismo signo el resultado es positivo; en caso contrario el resultado es negativo Aritmética binaria 17 Desventajas en signo-magnitud En el formato signo-magnitud existen dos ceros, uno positivo y otro negativo, pero con el mismo significado La multiplicación y la división pueden hacerse basándose en sumas y restas, pero es necesario tener circuitos capaces tanto de sumar como de restar Dado que las operaciones de suma y resta necesitan realizar comparaciones, los circuitos aritméticos en signo magnitud tienden a ser más lentos de lo deseado Aritmética binaria 18 9 Estructura del tema Introducción Operaciones aritméticas básicas Suma Resta Multiplicación División Representación de números enteros Signo-magnitud Complemento a 1 Complemento a 2 Resumen y bibliografía Aritmética binaria 19 Complemento a 1 El complemento a 1 de un número binario se obtiene cambiando todos los 0 por 1 y todos los 1 por 0 Los números positivos se representan igual que los números positivos en formato signo-magnitud Los números negativos son el complemento a 1 del correspondiente número positivo Aritmética binaria 0 0 0 1 0 1 0 1 1 1 1 0 1 0 1 0 –21 21 20 10 Valor decimal en complemento a 1 El valor decimal de los números positivos se calcula de la misma manera que en signo-magnitud 26 25 24 23 22 21 20 0 0 0 1 0 1 0 1 16 + 4 + 1 21 El valor decimal de los números negativos se calcula asignando el valor negativo del peso correspondiente al bit de signo y luego sumando uno al resultado –27 26 25 24 23 22 21 20 1 1 1 0 1 0 1 0 –128 + 64 + 32 + 8 + 2 –22 + 1 –21 Aritmética binaria 21 Rango de valores en complemento a 1 El bit más significativo de los números en formato complemento a 1 0 001 1 010 2 011 3 100 –3 Los números en complemento a 1 101 –2 pueden tener valores que van desde 110 –1 111 –0 Un número de n bits sólo dedicará n – 1) bits a representar la magnitud ( decimal 000 representa el signo binario n–1 –(2 Aritmética binaria n–1 – – 1) hasta +(2 1) 22 11 Generalizació Generalización: complemento a la base – 1 El complemento a la base menos uno de un número se calcula restándolo a la potencia de la base que se corresponde con la cantidad de dígitos del número y luego restando uno al resultado Sistema decimal Complemento a 9 Con 2 dígitos decimales 28 100 Sistema binario Complemento a 1 Con 3 bits 011(2) 1000(2) – 011(2) – 1 = 100(2) (10) (10) – 28(10) – 1 = 71(10) La conversión de un número a este formato se puede realizar de forma sencilla, dígito a dígito en binario se intercambian 0’s y 1’s: 011(2) en decimal se resta cada dígito a 9: 28(10) 100 71 (2) (10) Aritmética binaria 23 Generalizació Generalización: complemento a la base – 1 Representando los números negativos en complemento a la base menos uno se simplifica la operación de resta La resta de dos números se expresa como la suma de un número positivo y otro negativo El minuendo se mantiene positivo El sustraendo se pasa a negativo calculando su complemento a la base menos uno con 3 bits 011 (2) – 011(2) = 0(2) con 2 dígitos decimales Aritmética binaria 28 (10) 011 (2) + 100(2) = 111(2) = – 0 – 28(10) = 0(10) 28 (10) + 71 (10) = 99(10) = – 0 24 12 Aritmética en complemento a 1 La operación de resta es innecesaria: para restar podemos limitarnos a sumar el complemento a 1 del número que queremos restar Por ejemplo, suponiendo números de 8 bits (1 byte): 00011000 – 00011001 = 00011000 + 11100110 0 0 0 1 1 0 0 0 +1 1 1 0 0 1 1 0 1 1 1 1 1 1 1 0 24 – 25 = 24 + (–25) = –1 La multiplicación y la división también pueden realizarse partiendo de la suma Aritmética binaria 25 Aritmética en complemento a 1 La suma puede producir un acarreo en la última columna, que no puede representarse en 8 bits Para obtener el valor correcto debemos sumar este acarreo al resultado de la suma Por ejemplo, suponiendo de nuevo números de 8 bits: 00011001 – 00011000 = 00011001 + 11100111 + 0 0 0 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 + 0 0 0 0 0 0 0 1 Aritmética binaria 25 – 24 = 25 + (–24) = 1 26 13 Desbordamiento Dado que los números en un ordenador tienen una cantidad fija de bits, es posible un desbordamiento, es decir, que el resultado tenga demasiados bits Podremos identificar un resultado como incorrecto a causa de un desbordamiento porque no tendrá el signo que debería tener + 0 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 127 3 –125 Dos sumandos positivos no pueden sumar negativo Aritmética binaria 27 Desventajas del complemento a 1 En el formato complemento a 1 existen dos ceros, uno positivo y otro negativo, pero con el mismo significado La multiplicación, la división y la resta pueden hacerse basándose en sumas, pero los circuitos sumadores se complican porque en determinadas circunstancias hay que sumar un acarreo al resultado Debido a esta complicación, los circuitos aritméticos en complemento a 1 también tienden a ser más lentos de lo que se querría Aritmética binaria 28 14 Estructura del tema Introducción Operaciones aritméticas básicas Suma Resta Multiplicación División Representación de números enteros Signo-magnitud Complemento a 1 Complemento a 2 Resumen y bibliografía Aritmética binaria 29 Complemento a 2 El complemento a 2 de un número binario se obtiene sumando uno al bit menos significativo del complemento a 1 del número 0 0 0 1 0 1 0 1 1 1 1 0 1 0 1 0 + 1 1 1 1 0 1 0 1 1 21 –21 Un método alternativo es comenzar por el bit menos significativo hasta encontrar un 1 y luego hacer el complemento a 1 del resto del número Aritmética binaria 30 15 Valor decimal en complemento a 2 El valor decimal de los números positivos se calcula de la misma manera que en signo-magnitud 26 25 24 23 22 21 20 0 0 0 1 0 1 0 1 16 + 4 + 1 21 El valor decimal de los números negativos se calcula asignando el valor negativo del peso correspondiente al bit de signo –27 26 25 24 23 22 21 20 1 1 1 0 1 0 1 1 –128 + 64 + 32 + 8 + 2 + 1 –21 Aritmética binaria 31 Rango de valores en complemento a 2 El bit más significativo de los números en formato complemento a 2 representa el signo Un número de n bits sólo dedicará (n – 1) bits a representar la magnitud Los números en signo-magnitud pueden tener valores que van desde n–1 –(2n–1 ) hasta +(2 Aritmética binaria – 1) binario decimal 000 0 001 1 010 2 011 3 100 –4 101 –3 110 –2 111 –1 32 16 Generalización: complemento a la base El complemento a la base de un número se calcula restándolo a la potencia de la base correspondiente a la cantidad de dígitos del número Sistema decimal Complemento a 10 Con 2 dígitos decimales 28 100 Sistema binario Complemento a 2 Con 3 bits 011(2) 1000(2) – 011(2) = 101(2) (10) (10) – 28(10) = 72(10) Representando los números negativos en complemento a la base se simplifica la resta, permitiendo expresarla como la suma de un número positivo y otro negativo Con 3 bits 011 (2) – 011(2) = 0(2) Con 2 dígitos decimales 28 (10) 011 (2) + 101(2) = 1000(2) – 28(10) = 0(10) 28 (10) + 72 (10) = 100(10) Aritmética binaria 33 Ventajas del complemento a 2 Solo existe una representación del cero Todas las operaciones pueden hacerse con un circuito sumador, más simple que el usado por signo-magnitud o complemento a 1 y, por tanto, más rápido Por estos motivos, el complemento a 2 es el formato más utilizado por los ordenadores actuales Aritmética binaria binario signo-magnitud complemento a 1 complemento a 2 000 001 010 011 100 101 110 111 0 1 2 3 –0 –1 –2 –3 0 1 2 3 –3 –2 –1 –0 0 1 2 3 –4 –3 –2 –1 34 17 Suma en complemento a 2 Dado que el complemento a 2 es el formato más usado, estudiaremos su aritmética con más detalle Vamos a suponer que los números con los que trabajaremos tienen 8 bits (1 byte) A la hora de sumar dos números en complemento a 2, existen cuatro situaciones posibles Ambos números son positivos Los dos números tienen distinto signo ▫ El número positivo tiene un valor absoluto mayor que el negativo ▫ El número negativo tiene un valor absoluto mayor que el positivo Ambos números son negativos Aritmética binaria 35 Suma en complemento a 2 Si los dos valores sumados son positivos, el resultado también será positivo overflow), Existe la posibilidad de un desbordamiento ( es decir, de obtener un resultado incorrecto porque necesita más bits de los que se pueden representar 1 1 1 1 0 1 1 1 1 1 0 1 + 0 0 1 1 1 0 1 0 1 1 1 1 0 1 1 1 125 58 183 (max = 2 – 1 = 127) 7 Overflow!! El resultado debe ser positivo Aritmética binaria 36 18 Suma en complemento a 2 Si los dos valores sumados son negativos el resultado también será negativo carry) Existe la posibilidad de que aparezca un acarreo ( pero no invalida el resultado y debe descartarse 1 1 1 1 1 1 1 1 1 1 0 1 1 + 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0 1 –5 –6 –11 Carry!! Se descarta y el resultado es correcto Aritmética binaria 37 Suma en complemento a 2 Si los dos valores sumados son negativos también existe la posibilidad de que ocurra un desbordamiento y, por tanto, el resultado sea incorrecto 1 1 1 0 0 0 0 0 1 1 + 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 1 –125 –58 –183 (min = –2 = 128) 7 Overflow!! El resultado debe ser negativo Carry!! Se descarta Aritmética binaria 38 19 Suma en complemento a 2 Si los dos valores sumados tienen distinto signo es imposible que ocurra un desbordamiento Cuando el valor absoluto del número positivo es mayor que el del negativo puede aparecer un acarreo, pero se descarta y el resultado es correcto 1 1 1 1 0 0 1 1 1 0 0 1 + 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 57 –29 28 Carry!! Se descarta y el resultado es correcto Aritmética binaria 39 Resta en complemento a 2 Para restar dos números se calcula el complemento a 2 del número restado y se suman, descartando cualquiera acarreo que pueda aparecer y controlando la posibilidad de que ocurra un desbordamiento 57 – 29 = 57 + (– 29) = 28 1 1 1 1 0 0 1 1 1 0 0 1 + 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 57 –29 28 Carry!! Se descarta y el resultado es correcto Aritmética binaria 40 20 Resta en complemento a 2 Para restar dos números se calcula el complemento a 2 del número restado y se suman, descartando cualquiera acarreo que pueda aparecer y controlando la posibilidad de que ocurra un desbordamiento –125 – 58 = –125 + (– 58) = –183 1 –125 –58 –183 (min = –2 = 128) 1 1 0 0 0 0 0 1 1 + 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 1 7 Overflow!! El resultado debe ser negativo Carry!! Se descarta Aritmética binaria 41 Sumas o restas en cadena Para sumar o restar varios números aplicamos la propiedad asociativa, es decir, sumamos o restamos los números de dos en dos 68 + 27 + 14 + 18 = ( (68 + 27) + 14) + 18 = 127 0 + 0 0 + 0 0 0 0 1 0 1 0 1 0 1 Aritmética binaria 0 0 0 0 1 0 1 0 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 0 1 68 27 95 14 109 18 127 42 21 Multiplicación en complemento a 2 La suma directa es el método más simple: sumar el multiplicando tantas veces como el multiplicador La desventaja de este método es que puede llegar a ser muy lento si el multiplicador es muy grande El método más común es el de los productos parciales Se multiplica el multiplicando por cada bit del multiplicador Cada producto parcial se desplaza un bit a la izquierda La suma de los productos parciales nos da el resultado Aritmética binaria 43 Multiplicación en complemento a 2 El signo del resultado depende de los signos de los números multiplicados Si son del mismo signo, el resultado es positivo Si son de distinto signo, el resultado es negativo Después de comprobar los signos, los números a multiplicar deben ser pasados a binario real Es bastante posible que el resultado tenga más bits que la representación de los operandos 3x3=9 Aritmética binaria 11 x 11 = 1001 44 22 Multiplicación en complemento a 2 Ejemplo: 83 X –59 = –4897 Los números tienen distinto signo, luego el resultado será un número negativo 83 = 01010011 –59 = 11000101 Pasamos los números a binario real Ignoramos el bit de signo del número positivo Deshacemos el complemento a 2 del número negativo y luego ignoramos el bit de signo 83 = 01010011 –59 = 11000101 59 = 00111011 Aritmética binaria 45 Multiplicación en complemento a 2 Realizamos la multiplicación entre los dos números positivos + + 1 + 1 1 0 Aritmética binaria + 1 1 1 0 0 0 0 1 0 1 0 1 0 x0 0 1 1 0 + 1 0 1 1 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 0 0 0 1 1 1 1 0 1 1 1 1 0 1 0 0 1 0 0 0 1 0 0 0 0 1 46 23 Multiplicación en complemento a 2 Multiplicando números de 8 bits hemos obtenido un resultado de 13 bits Supondremos que el resultado tiene 16 bits Será importante recordar esto para diseñar multiplicadores Dado que hemos multiplicado dos números positivos, el bit de signo debe ser positivo o habrá habido un desbordamiento 0001001100100001 Una vez obtenido el resultado, y dado que habíamos determinado que éste era negativo, calculamos el complemento a 2 del mismo 0001001100100001 1110110011011111 Aritmética binaria 47 División en complemento a 2 El esquema básico de división usado en los ordenadores está basado en la resta Dado que las restas en complemento a 2 son sumas, la división puede realizarse con circuitos sumadores El signo del resultado depende de los signos de los dos operandos de la división Si son del mismo signo, el resultado es positivo Si son de distinto signo, el resultado es negativo Tras comprobar los signos, cualquier número negativo debe ser convertido en el positivo corresponidente Aritmética binaria 48 24 División en complemento a 2 Ejemplo: 100 / 25 = 4 Los números tienen el mismo signo, luego el resultado será un número positivo 100 = 01100100 25 = 00011001 En caso de que alguno de ellos hubiera sido un número negativo hubiéramos tenido que deshacer el complemento a 2 El valor inicial del cociente es cero C=0 Aritmética binaria 49 División en complemento a 2 ) Restamos el divisor del dividendo (sumando su complemento a 2 para obtener el primer resto parcial y luego sumamos uno al cociente 01100100 – 00011001 01100100 + 11100111 = 101001011 C=C+1=0+1=1 Si el resto parcial es cero o negativo, damos la división por finalizada Si el resto parcial es positivo, repetimos el proceso, restando el divisor del resto parcial y volviendo a sumar uno al cociente Aritmética binaria 50 25 División en complemento a 2 Segunda iteración: 01001011 – 00011001 01001011 + 11100111 = 100110010 C = C + 1 = 1 + 1 = 10 Tercera iteración: 00110010 – 00011001 00110010 + 11100111 = 100011001 C = C + 1 = 10 + 1 = 11 Aritmética binaria 51 División en complemento a 2 Cuarta iteración: 00011001 – 00011001 00011001 + 11100111 = 100000000 C = C + 1 = 11 + 1 = 100 El resto parcial es cero, por lo que la división termina Sólo queda asegurarse de que el bit de signo es el correcto, en este caso, signo positivo C = 100 7 bits magnitud 1 bit de signo positivo Aritmética binaria C = 0000100 C = 00000100 52 26 Estructura del tema Introducción Operaciones aritméticas básicas Suma Resta Multiplicación División Representación de números enteros Signo-magnitud Complemento a 1 Complemento a 2 Resumen y bibliografía Aritmética binaria 53 Resumen La comprensión de las operaciones básicas de la aritmética binaria es importante para el diseño de los circuitos digitales que las realizan Existen varios formatos que permiten la representación de números enteros negativos Los ordenadores actuales utilizan generalmente el formato de complemento a 2 para representar números negativos porque permite simplificar en gran medida el diseño de los circuitos necesarios Aritmética binaria 54 27 Bibliografía Fundamentos de Sistemas Digitales (7ª edición) Capítulo 2 Thomas L. Floyd Prentice Hall, 2000 Principios de Diseño Digital Capítulo 2 Daniel D. Gajski Prentice Hall, 1997 Aritmética binaria 55 28